2025年53精准练九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. [2024晋中模拟]普救寺位于山西省运城市永济市,是我国历史名剧《西厢记》故事的发生地,寺庙规模宏伟,内部有很多著名建筑.其中,最著名的便是莺莺塔.数学兴趣小组根据光的反射定律(如图),把一面镜子放在离古塔(CD)72 m的点P处,然后观测者沿着直线CP后退到点B处,这时恰好在镜子里看到塔顶端D,量得BP = 3 m,已知观测者目高AB = 1.5 m,那么该古塔(CD)的高度是______ m.


答案:
36
2. 如图,文文应用所学的相似三角形相关知识测量某塔的高度,她站在距离塔底中心A点120 m的D点处,测得自己的影长DE为0.4 m,此时该塔的影子的顶端为点C,她测得点D与点C的距离为23 m,已知文文的身高DF为1.6 m,求该塔的高AB.(图中各点都在同一平面内,且点A,C,D,E在同一直线上)


答案:
解:
∵$AD = 120\ m$,$CD = 23\ m$,
∴$AC = AD - CD = 97\ m$,
由题意得$BC// FE$,
∴$\angle BCA=\angle FED$,
由题意得$AB\perp AC$,$DF\perp AE$,
∴$\angle BAC=\angle FDE = 90^{\circ}$,
∴$\triangle ABC\sim\triangle DFE$,
∴$\frac{AB}{AC}=\frac{DF}{DE}$,即$\frac{AB}{97}=\frac{1.6}{0.4}$,
解得$AB = 388$,
∴该塔的高$AB$为$388\ m$.
∵$AD = 120\ m$,$CD = 23\ m$,
∴$AC = AD - CD = 97\ m$,
由题意得$BC// FE$,
∴$\angle BCA=\angle FED$,
由题意得$AB\perp AC$,$DF\perp AE$,
∴$\angle BAC=\angle FDE = 90^{\circ}$,
∴$\triangle ABC\sim\triangle DFE$,
∴$\frac{AB}{AC}=\frac{DF}{DE}$,即$\frac{AB}{97}=\frac{1.6}{0.4}$,
解得$AB = 388$,
∴该塔的高$AB$为$388\ m$.
3. [2024晋中期中]人字梯也称折梯,是用于在平面上方空间工作的一种登高工具,因使用时其左、右梯杆及地面构成一个等腰三角形,看起来像一个“人”字,因而把它形象地称为“人字梯”,如图①所示.图②是其示意图,已知AB = AC,拉杆EF//BC,AE = $\frac{2}{5}AB$.若EF = 1米,则两梯杆底端B,C之间的距离为 ( )

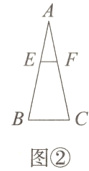
A. 2米
B. 2.1米
C. 2.5米
D. $\frac{10}{3}$米

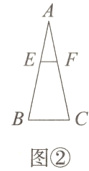
A. 2米
B. 2.1米
C. 2.5米
D. $\frac{10}{3}$米
答案:
C
4. 一把剪刀如图所示,AB = 2BC,BD = 2BE,当手握的地方张开3cm(EC = 3cm)时,剪刀的尖端A,D两点的距离为________ cm.


答案:
6
5. 如图,一条河的两岸有一段是平行的,在河的南岸边每隔4米有一棵树,在河的北岸边每隔50米有一根电线杆,小丽站在离南岸边12米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有两棵树,则河宽为________米.


答案:
38
6. [2023南京期末]如图,在A时测得某树的影长为8 m,B时又测得该树的影长为2 m,若两时刻日照的光线互相垂直,则树的高度为 ( )

A. 2 m
B. 4 m
C. 6 m
D. 8 m

A. 2 m
B. 4 m
C. 6 m
D. 8 m
答案:
B
查看更多完整答案,请扫码查看


