《2025年53精准练九年级数学下册人教版山西专版》

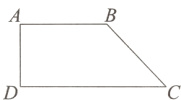
1. [2024深圳福田区模拟]人体工学椅的座垫高度应满足人的双脚能平放于地面，且腿的弯曲角度为90°.如图是一人体工学椅的实物图和示意图，若AD = 40 cm，∠C = 50°，则该椅子座垫高度还要增加多少厘米，才符合人体工学椅的要求（ ）


A. 40sin50° - 40
B. 40cos50° - 40
C. $\frac{40}{\sin50^{\circ}} - 40$
D. $\frac{40}{\cos50^{\circ}} - 40$

答案： C

2. [2024惠州模拟]某县消防大队到某小区进行消防演习.图1是一辆云梯消防车的实物图，图2是其工作示意图，起重臂AC可伸缩（15m≤AC≤26m），且起重臂AC可绕点A在一定范围内转动，张角为∠CAE（90°≤∠CAE≤150°），点A距离地面BD的高度AE为3m.当起重臂AC的长度为20m，张角∠CAE = 127°时，求云梯消防车最高点C距离地面BD的高度CF.(参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，$\sqrt{3}\approx1.73$)

答案：
解:过点A作AG⊥CF,垂足为G,

∴∠AEF = ∠AGF = ∠GFE = 90°,
∴四边形AEFG是矩形,
∴AE = FG = 3m,∠EAG = 90°,
∵∠CAE = 127°,
∴∠CAG = ∠CAE - ∠EAG = 127° - 90° = 37°,
在Rt△AGC中,AC = 20 m,
∴CG = AC·sin37°≈20×0.60 = 12(m),
∴CF = CG + GF = 12 + 3 = 15(m),
∴云梯消防车最高点C距离地面BD的高度CF为15 m.

3. [2024武威]习近平总书记于2021年指出，中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富，风力发电发展迅速.某学习小组成员查阅资料得知，在风力发电机组中，“风电塔筒”非常重要，它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图，已知一风电塔筒AH垂直于地面，测角仪CD，EF在AH两侧，CD = EF = 1.6 m，点C与点E相距182 m(点C，H，E在同一条直线上)，在D处测得筒尖顶点A的仰角为45°，在F处测得筒尖顶点A的仰角为53°.求风电塔筒AH的高度.(参考数据：sin53°≈$\frac{4}{5}$，cos53°≈$\frac{3}{5}$，tan53°≈$\frac{4}{3}$)

答案：
解:如图所示,连接DF交AH于G,易得四边形CDGH、EFGH是矩形,

∴GH = CD = 1.6 m,DG = CH,FG = HE,
∴DF = DG + FG = CH + HE = CE = 182 m,
设AG = x m,
在Rt△ADG中,tan∠ADG = $\frac{AG}{DG}$,
∴tan45° = $\frac{x}{DG}$,
∴DG = x m,
在Rt△AFG中,tan∠AFG = $\frac{AG}{FG}$,
∴tan53° = $\frac{x}{FG}$,
∴FG≈$\frac{3}{4}x$ m,
∴x + $\frac{3}{4}x$ = 182,解得x = 104,
∴AG = 104 m,
∴AH = AG + GH = 105.6 m,
∴风电塔筒AH的高度为105.6 m.