2025年53精准练九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,在Rt△ABC中,∠C = 90°,AB = 4,AC = 2√3,则∠B的度数为( )

A. 30°
B. 45°
C. 60°
D. 90°

A. 30°
B. 45°
C. 60°
D. 90°
答案:
C
2. 在Rt△ABC中,∠C = 90°,AC = 6,BC = 2√3,则∠A = ______°,AB = ______.
答案:
30; 4$\sqrt{3}$
3. [教材P77习题1变式]在Rt△ABC中,∠C = 90°,∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件解直角三角形:
(1) a = √6,c = 2√3;
(2) a = 1/3,b = √3/9.
(1) a = √6,c = 2√3;
(2) a = 1/3,b = √3/9.
答案:
解:
(1)在Rt△ABC中,由勾股定理得,
$b = \sqrt{c^{2}-a^{2}}=\sqrt{(2\sqrt{3})^{2}-(\sqrt{6})^{2}}=\sqrt{6}$.
在Rt△ABC中, $\sin A=\frac{a}{c}=\frac{\sqrt{6}}{2\sqrt{3}}=\frac{\sqrt{2}}{2}$,
$\therefore \angle A = 45^{\circ}$,
$\therefore \angle B = 45^{\circ}$.
(2)在Rt△ABC中,由勾股定理得,
$c = \sqrt{a^{2}+b^{2}}=\sqrt{(\frac{1}{3})^{2}+(\frac{\sqrt{3}}{9})^{2}}=\frac{2\sqrt{3}}{9}$.
在Rt△ABC中, $\sin B=\frac{b}{c}=\frac{\frac{\sqrt{3}}{9}}{\frac{2\sqrt{3}}{9}}=\frac{1}{2}$,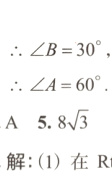
$\therefore \angle B = 30^{\circ}$,
$\therefore \angle A = 60^{\circ}$.
解:
(1)在Rt△ABC中,由勾股定理得,
$b = \sqrt{c^{2}-a^{2}}=\sqrt{(2\sqrt{3})^{2}-(\sqrt{6})^{2}}=\sqrt{6}$.
在Rt△ABC中, $\sin A=\frac{a}{c}=\frac{\sqrt{6}}{2\sqrt{3}}=\frac{\sqrt{2}}{2}$,
$\therefore \angle A = 45^{\circ}$,
$\therefore \angle B = 45^{\circ}$.
(2)在Rt△ABC中,由勾股定理得,
$c = \sqrt{a^{2}+b^{2}}=\sqrt{(\frac{1}{3})^{2}+(\frac{\sqrt{3}}{9})^{2}}=\frac{2\sqrt{3}}{9}$.
在Rt△ABC中, $\sin B=\frac{b}{c}=\frac{\frac{\sqrt{3}}{9}}{\frac{2\sqrt{3}}{9}}=\frac{1}{2}$,
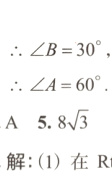
$\therefore \angle B = 30^{\circ}$,
$\therefore \angle A = 60^{\circ}$.
4. 在△ABC中,∠C = 90°,AB = 6,∠A = 60°,则AC的长为( )
A. 3
B. 3√2
C. 3√3
D. 2√3
A. 3
B. 3√2
C. 3√3
D. 2√3
答案:
A
5. 在△ABC中,∠C = 90°,BC = 24,∠B = 30°,则AC = _________.
答案:
$8\sqrt{3}$
6. [教材P77习题1变式]在Rt△ABC中,∠C = 90°,∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件解直角三角形:
(1) c = 5,∠B = 45°;
(2) b = 15,∠B = 60°.
(1) c = 5,∠B = 45°;
(2) b = 15,∠B = 60°.
答案:
解:
(1) 在Rt△ABC中, $\angle C = 90^{\circ}$, $\angle B = 45^{\circ}$,
$\therefore \angle A = 45^{\circ}$.
$\because \sin B=\frac{b}{c}$, $c = 5$,
$\therefore b = c\cdot\sin B = 5\times\sin 45^{\circ}=\frac{5\sqrt{2}}{2}$.
$\because \cos B=\frac{a}{c}$, $c = 5$,
$\therefore a = c\cdot\cos B = 5\times\cos 45^{\circ}=\frac{5\sqrt{2}}{2}$.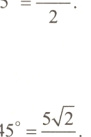
(2)在Rt△ABC中, $\angle C = 90^{\circ}$, $\angle B = 60^{\circ}$
$\therefore \angle A = 30^{\circ}$.
$\because \sin B=\frac{b}{c}$, $b = 15$,
$\therefore c=\frac{b}{\sin B}=\frac{15}{\sin 60^{\circ}} = 10\sqrt{3}$.
$\because \tan B=\frac{b}{a}$, $b = 15$,
$\therefore a=\frac{b}{\tan B}=\frac{15}{\tan 60^{\circ}} = 5\sqrt{3}$.
解:
(1) 在Rt△ABC中, $\angle C = 90^{\circ}$, $\angle B = 45^{\circ}$,
$\therefore \angle A = 45^{\circ}$.
$\because \sin B=\frac{b}{c}$, $c = 5$,
$\therefore b = c\cdot\sin B = 5\times\sin 45^{\circ}=\frac{5\sqrt{2}}{2}$.
$\because \cos B=\frac{a}{c}$, $c = 5$,
$\therefore a = c\cdot\cos B = 5\times\cos 45^{\circ}=\frac{5\sqrt{2}}{2}$.
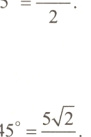
(2)在Rt△ABC中, $\angle C = 90^{\circ}$, $\angle B = 60^{\circ}$
$\therefore \angle A = 30^{\circ}$.
$\because \sin B=\frac{b}{c}$, $b = 15$,
$\therefore c=\frac{b}{\sin B}=\frac{15}{\sin 60^{\circ}} = 10\sqrt{3}$.
$\because \tan B=\frac{b}{a}$, $b = 15$,
$\therefore a=\frac{b}{\tan B}=\frac{15}{\tan 60^{\circ}} = 5\sqrt{3}$.
7. 如图,在△ABC中,BD⊥AC,垂足为D,AB = 6,AC = 5√3,∠A = 30°.
(1) 求BD和AD的长;
(2) 求tan C的值.

(1) 求BD和AD的长;
(2) 求tan C的值.

答案:
解:
(1) $\because BD\perp AC$,
$\therefore \angle ADB = 90^{\circ}$,
在Rt△ABD中, $AB = 6$, $\angle A = 30^{\circ}$,
$\therefore BD = AB\cdot\sin A = 6\times\sin 30^{\circ}=3$,
$AD = AB\cdot\cos A = 6\times\cos 30^{\circ}=3\sqrt{3}$.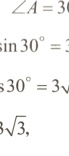
(2) $\because AC = 5\sqrt{3}$, $AD = 3\sqrt{3}$,
$\therefore CD = AC - AD = 2\sqrt{3}$,
在Rt△CBD中,
$\because \angle CDB = 90^{\circ}$, $BD = 3$, $CD = 2\sqrt{3}$,
$\therefore \tan C=\frac{BD}{CD}=\frac{3}{2\sqrt{3}}=\frac{\sqrt{3}}{2}$.
解:
(1) $\because BD\perp AC$,
$\therefore \angle ADB = 90^{\circ}$,
在Rt△ABD中, $AB = 6$, $\angle A = 30^{\circ}$,
$\therefore BD = AB\cdot\sin A = 6\times\sin 30^{\circ}=3$,
$AD = AB\cdot\cos A = 6\times\cos 30^{\circ}=3\sqrt{3}$.
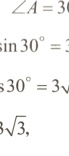
(2) $\because AC = 5\sqrt{3}$, $AD = 3\sqrt{3}$,
$\therefore CD = AC - AD = 2\sqrt{3}$,
在Rt△CBD中,
$\because \angle CDB = 90^{\circ}$, $BD = 3$, $CD = 2\sqrt{3}$,
$\therefore \tan C=\frac{BD}{CD}=\frac{3}{2\sqrt{3}}=\frac{\sqrt{3}}{2}$.
查看更多完整答案,请扫码查看


