《2025年53精准练九年级数学下册人教版山西专版》

8.[2024晋中榆社县二模]如图，点A在反比例函数$y=\frac{2}{x}(x ＞ 0)$的图象上，点B在反比例函数$y=\frac{6}{x}(x ＞ 0)$的图象上，且AB//x轴，BC⊥x轴于点C，连接OA，则四边形ABCO的面积为( )

A. 5
B. 4
C. 7
D. 2

答案： A

9.[分类讨论]如图，在平面直角坐标系中，反比例函数$y=\frac{k}{x}(x ＜ 0)$的图象经过点A(-4, 3)，将点A向右平移2个单位，再向上平移a个单位得到点B，此时点B恰好落在反比例函数$y=\frac{k}{x}(x ＜ 0)$的图象上，过A，B两点的直线与y轴交于点C，与x轴交于点D。
(1)求点C的坐标；
(2)点P为△COD直角边上的一个动点，连接AP，BP，当△ABP的面积为5时，请直接写出点P的坐标。

答案： 解：
(1) 将$A(-4,3)$代入$y = \frac{k}{x}$，
得$k = -4\times3 = -12$，
$\therefore$反比例函数的表达式为$y = -\frac{12}{x}$.
$\because$将点$A$向右平移$2$个单位，再向上平移$a$个单位得到点$B$，
$\therefore$点$B$的横坐标为$-2$.
$\because$点$B$在反比例函数$y = -\frac{12}{x}$的图象上，$\therefore$当$x = -2$时，$y = \frac{-12}{-2} = 6$.
$\therefore B(-2,6)$.
设直线$AB$的表达式为$y = mx + n$，
将$A(-4,3)$，$B(-2,6)$代入，
得$\begin{cases}-4m + n = 3,\\-2m + n = 6,\end{cases}$
解得$\begin{cases}m = \frac{3}{2},\\n = 9,\end{cases}$
$\therefore$直线$AB$的表达式为$y = \frac{3}{2}x + 9$.
令$x = 0$，得$y = 9$，
$\therefore C(0,9)$.
(2) 点$P$的坐标为$(0,4)$或$(-\frac{8}{3},0)$.
详解：分两种情况讨论：
当点$P$在$OC$上时，如图.
设点$P$的坐标为$(0,y)$，则$CP = 9 - y$，
$\therefore S_{\triangle ABP} = S_{\triangle ACP} - S_{\triangle BCP} = \frac{1}{2}CP\times4 - \frac{1}{2}CP\times2 = \frac{1}{2}\times(9 - y)\times2 = 5$，
$\therefore y = 4$，此时点$P$的坐标为$(0,4)$.
当点$P$在$OD$上时，如图.
设点$P$的坐标为$(x,0)$，则$DP = x + 6$，
$\therefore S_{\triangle ABP} = S_{\triangle BDP} - S_{\triangle ADP} = \frac{1}{2}DP\times6 - \frac{1}{2}DP\times3 = \frac{1}{2}\times(x + 6)\times3 = 5$，
$\therefore x = -\frac{8}{3}$，此时点$P$的坐标为$(-\frac{8}{3},0)$.
故点$P$的坐标为$(0,4)$或$(-\frac{8}{3},0)$.

10.[应用意识]请解答下列题目。
问题探究
启知学习小组在课外学习时，得出了这样一个结论：如图1，在四边形ABCD中，连接AC，BD，如果△ABC与△BCD的面积相等，那么AD//BC。
在小组交流时，他们在图1中添加了如图所示的辅助线，AE⊥BC于点E，DF⊥BC于点F。
请你完成证明该结论的过程。

答案： 解：问题探究
证明：$\because AE\perp BC$于点$E$，$DF\perp BC$于点$F$，
$\therefore S_{\triangle ABC} = \frac{1}{2}BC\cdot AE$，$S_{\triangle BCD} = \frac{1}{2}BC\cdot DF$.
$\because S_{\triangle ABC} = S_{\triangle BCD}$，
$\therefore AE = DF$.
$\because AE\perp BC$，$DF\perp BC$，
$\therefore AE// DF$，
$\therefore$四边形$AEFD$是平行四边形，
$\therefore AD// BC$.
结论应用
(1) $\because A(1,4)$，
$\therefore 4 = \frac{m}{1}$，
解得$m = 4$，
$\therefore$反比例函数的表达式为$y = \frac{4}{x}$.

结论应用
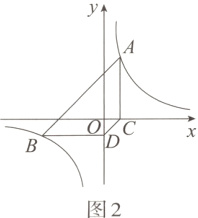
在平面直角坐标系中，反比例函数$y=\frac{m}{x}(m≠0)$的图象经过A(1, 4)，B(a, b)两点，过点A作AC⊥x轴于点C，过点B作BD⊥y轴于点D。
(1)求反比例函数的表达式；
(2)如图2，若点B在第三象限，判断并证明CD与AB的位置关系。

答案：
(2) $CD// AB$.
证明：如图，连接$AD$，$BC$，延长$BD$，$AC$相交于点$M$，
$\because A(1,4)$，$B(a,b)$，
$\therefore M(1,b)$，$BM = 1 - a$，$AM = 4 - b$
且$b = \frac{4}{a}$，$\therefore S_{\triangle ABC} = \frac{1}{2}AC\cdot BM = \frac{1}{2}\times4\times(1 - a) = 2(1 - a)$，$S_{\triangle ABD} = \frac{1}{2}BD\cdot AM = \frac{1}{2}\times(-a)\times(4 - b) = \frac{1}{2}\times(-a)\times(4 - \frac{4}{a}) = 2(1 - a)$，
$\therefore S_{\triangle ABC} = S_{\triangle ABD}$，
$\therefore CD// AB$.