2025年53精准练九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
12.若$\tan A = 2$,则估计$\angle A$的度数( )
A.在$0^{\circ}$和$30^{\circ}$之间
B.在$30^{\circ}$和$45^{\circ}$之间
C.在$45^{\circ}$和$60^{\circ}$之间
D.在$60^{\circ}$和$90^{\circ}$之间
A.在$0^{\circ}$和$30^{\circ}$之间
B.在$30^{\circ}$和$45^{\circ}$之间
C.在$45^{\circ}$和$60^{\circ}$之间
D.在$60^{\circ}$和$90^{\circ}$之间
答案:
D
13.如图,$\triangle ABC$的顶点$B$、$C$的坐标分别是$(1,0)$、$(0,\sqrt{3})$,且$\angle ABC = 90^{\circ}$,$\angle A = 30^{\circ}$,则顶点$A$的坐标是__________.


答案:
$(4,\sqrt{3})$
14.[2024晋中平遥县二模改编]已知锐角$A$,$B$满足$\sin(4\angle A - 5\angle B)=\frac{1}{2}$,$\tan(2\angle A - \angle B)=\sqrt{3}$,则$(\frac{1}{2})^{-2}+2\sin A - (\sqrt{2}-1)^{0}-\sqrt[3]{27}-\tan^{2}B$的值为__________.
答案:
$\sqrt{2}-\frac{1}{3}$
15.在$\triangle ABC$中,若$\left|\sin A - \frac{\sqrt{2}}{2}\right|+(\frac{\sqrt{3}}{2}-\cos B)^{2}=0$,$\angle B$,$\angle A$都是锐角,求$\angle C$的度数.
答案:
解:$\because|\sin A-\frac{\sqrt{2}}{2}|+(\frac{\sqrt{3}}{2}-\cos B)^{2}=0$,
$\therefore\sin A=\frac{\sqrt{2}}{2},\cos B=\frac{\sqrt{3}}{2}$,
$\because\angle B,\angle A$都是锐角,
$\therefore\angle A = 45^{\circ},\angle B = 30^{\circ}$,
$\therefore\angle C = 180^{\circ}-45^{\circ}-30^{\circ}=105^{\circ}$.
$\therefore\sin A=\frac{\sqrt{2}}{2},\cos B=\frac{\sqrt{3}}{2}$,
$\because\angle B,\angle A$都是锐角,
$\therefore\angle A = 45^{\circ},\angle B = 30^{\circ}$,
$\therefore\angle C = 180^{\circ}-45^{\circ}-30^{\circ}=105^{\circ}$.
16.在$\triangle ABC$中,已知$\angle A = 60^{\circ}$,$\angle B$为锐角,且$\tan A$,$\cos B$恰为一元二次方程$2x^{2}-3mx + 3 = 0$的两个实数根.求$m$的值并判断$\triangle ABC$的形状.
答案:
解:$\because\angle A = 60^{\circ}$,
$\therefore\tan A=\sqrt{3}$,
把$x = \sqrt{3}$代入方程$2x^{2}-3mx + 3 = 0$,
得$2\times(\sqrt{3})^{2}-3\sqrt{3}m + 3 = 0$,
解得$m=\sqrt{3}$,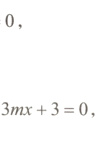
把$m=\sqrt{3}$代入方程$2x^{2}-3mx + 3 = 0$,
得$2x^{2}-3\sqrt{3}x + 3 = 0$,
解得$x_{1}=\sqrt{3},x_{2}=\frac{\sqrt{3}}{2}$.
$\therefore\cos B=\frac{\sqrt{3}}{2},\therefore\angle B = 30^{\circ}$,
$\therefore\angle C = 180^{\circ}-\angle A-\angle B = 90^{\circ}$,
$\therefore\triangle ABC$是直角三角形.
解:$\because\angle A = 60^{\circ}$,
$\therefore\tan A=\sqrt{3}$,
把$x = \sqrt{3}$代入方程$2x^{2}-3mx + 3 = 0$,
得$2\times(\sqrt{3})^{2}-3\sqrt{3}m + 3 = 0$,
解得$m=\sqrt{3}$,
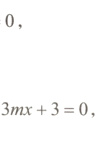
把$m=\sqrt{3}$代入方程$2x^{2}-3mx + 3 = 0$,
得$2x^{2}-3\sqrt{3}x + 3 = 0$,
解得$x_{1}=\sqrt{3},x_{2}=\frac{\sqrt{3}}{2}$.
$\therefore\cos B=\frac{\sqrt{3}}{2},\therefore\angle B = 30^{\circ}$,
$\therefore\angle C = 180^{\circ}-\angle A-\angle B = 90^{\circ}$,
$\therefore\triangle ABC$是直角三角形.

17.[推理能力]观察下列等式:
①$\sin 30^{\circ}=\frac{1}{2}$,$\cos 60^{\circ}=\frac{1}{2}$;
②$\sin 45^{\circ}=\frac{\sqrt{2}}{2}$,$\cos 45^{\circ}=\frac{\sqrt{2}}{2}$;
③$\sin 60^{\circ}=\frac{\sqrt{3}}{2}$,$\cos 30^{\circ}=\frac{\sqrt{3}}{2}$.
(1)根据上述规律,计算$\sin^{2}\alpha+\sin^{2}(90^{\circ}-\alpha)=$__________;
(2)计算:$\sin^{2}1^{\circ}+\sin^{2}2^{\circ}+\sin^{2}3^{\circ}+\cdots+\sin^{2}89^{\circ}$.
①$\sin 30^{\circ}=\frac{1}{2}$,$\cos 60^{\circ}=\frac{1}{2}$;
②$\sin 45^{\circ}=\frac{\sqrt{2}}{2}$,$\cos 45^{\circ}=\frac{\sqrt{2}}{2}$;
③$\sin 60^{\circ}=\frac{\sqrt{3}}{2}$,$\cos 30^{\circ}=\frac{\sqrt{3}}{2}$.
(1)根据上述规律,计算$\sin^{2}\alpha+\sin^{2}(90^{\circ}-\alpha)=$__________;
(2)计算:$\sin^{2}1^{\circ}+\sin^{2}2^{\circ}+\sin^{2}3^{\circ}+\cdots+\sin^{2}89^{\circ}$.
答案:
解:
(1)1.
(2)由
(1)中结论可得,
$\sin^{2}1^{\circ}+\sin^{2}2^{\circ}+\sin^{2}3^{\circ}+\cdots+\sin^{2}89^{\circ}$
$=(\sin^{2}1^{\circ}+\sin^{2}89^{\circ})+(\sin^{2}2^{\circ}+\sin^{2}88^{\circ})+\cdots+\sin^{2}45^{\circ}$
$=1 + 1+\cdots+1+\frac{1}{2}$
$=44+\frac{1}{2}$
$=\frac{89}{2}$.
(1)1.
(2)由
(1)中结论可得,
$\sin^{2}1^{\circ}+\sin^{2}2^{\circ}+\sin^{2}3^{\circ}+\cdots+\sin^{2}89^{\circ}$
$=(\sin^{2}1^{\circ}+\sin^{2}89^{\circ})+(\sin^{2}2^{\circ}+\sin^{2}88^{\circ})+\cdots+\sin^{2}45^{\circ}$
$=1 + 1+\cdots+1+\frac{1}{2}$
$=44+\frac{1}{2}$
$=\frac{89}{2}$.
查看更多完整答案,请扫码查看


