2025年53精准练九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. [2024阳泉三模]如图,在平面直角坐标系中,△OAB与△OCD位似,相似比是2,若点A(-3,2),B(-2,-2),则点B的对应点D的坐标为 ( )
A. (-1,-1)
B. (-4,-4)
C. (-1,-1)或(1,1)
D. (-4,-4)或(-1,-1)
A. (-1,-1)
B. (-4,-4)
C. (-1,-1)或(1,1)
D. (-4,-4)或(-1,-1)
答案:
C
11. [2023临汾洪洞县期中]图①、图②、图③都是6×6的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.点A,B,C均在格点上.在图①、图②、图③给定的网格中,仅用无刻度的直尺,按下列要求完成作图,并保留作图痕迹.
(1)在图①中,以点C为位似中心,将△ABC的各边放大到原来的2倍;
(2)在图②中,在线段BC上找一点D,使得CD = 3BD;
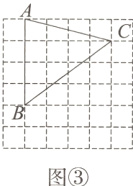
(3)在图③中,作△BEF,使△BEF∽△BAC,且相似比为$\frac{3}{4}$.


(1)在图①中,以点C为位似中心,将△ABC的各边放大到原来的2倍;
(2)在图②中,在线段BC上找一点D,使得CD = 3BD;
(3)在图③中,作△BEF,使△BEF∽△BAC,且相似比为$\frac{3}{4}$.



答案:
(1) 如图①,$\triangle A'B'C$即为所求.
(2) 如图②, 点$D$即为所求. 提示: 取格点$M$,$N$, 连接$MN$交$BC$于点 可知$\triangle BDM\sim\triangle CDN$, $\therefore \frac{BD}{CD}=\frac{BM}{CN}=\frac{1}{3}$, $\therefore CD = 3BD$.
(3) 如图③,$\triangle BEF$即为所求.\frac{BE}{AB}$\frac{3}{4}$" page="11" src="https://thumb.zyjl.cn/pdf/12/page_98.jpg?x-oss-process=image/crop,x_408,y_1372,w_91,h_133/contrast,3">$\because \triangle BEF\sim\triangle BAC$, 且相似比为$\frac{3}{4}$,$\therefore \frac{BE}{AB}=\frac{BF}{BC}=\frac{3}{4}$.
(1) 如图①,$\triangle A'B'C$即为所求.
(2) 如图②, 点$D$即为所求. 提示: 取格点$M$,$N$, 连接$MN$交$BC$于点 可知$\triangle BDM\sim\triangle CDN$, $\therefore \frac{BD}{CD}=\frac{BM}{CN}=\frac{1}{3}$, $\therefore CD = 3BD$.
(3) 如图③,$\triangle BEF$即为所求.\frac{BE}{AB}$\frac{3}{4}$" page="11" src="https://thumb.zyjl.cn/pdf/12/page_98.jpg?x-oss-process=image/crop,x_408,y_1372,w_91,h_133/contrast,3">$\because \triangle BEF\sim\triangle BAC$, 且相似比为$\frac{3}{4}$,$\therefore \frac{BE}{AB}=\frac{BF}{BC}=\frac{3}{4}$.
12. [2024临汾一模]阅读与思考
下面是一位同学的数学学习笔记,请仔细阅读并完成相应的任务.
连接三角形顶点和它对边中点的线段叫做三角形的中线,三角形的三条中线相交于一点,这个点叫做三角形的重心.研究发现,三角形的重心把中线分成长度比为1:2的两部分,用数学语言表述为:如图1,在△ABC中,中线AD,CE相交于点G,则EG = $\frac{1}{2}CG$,DG = $\frac{1}{2}AG$.
证明:连接DE.
∵D,E分别是边BC,AB的中点,
∴____________________.
∴DE//AC,且DE = $\frac{1}{2}AC$.(依据)
∴∠DEC = ∠ACE,∠EDA = ∠DAC.
……

任务:
(1)材料中横线部分应填写的结论为____________________;材料中“依据”的定理内容是____________________.
(2)请将材料中的证明过程补充完整.
(3)如图2,在△MNH中,点K,L分别在边MN,MH上,连接HK,NL交于点F.若MK = $\frac{1}{3}MN$,ML = $\frac{1}{3}MH$,则KF与HF的数量关系为____________________.

下面是一位同学的数学学习笔记,请仔细阅读并完成相应的任务.
连接三角形顶点和它对边中点的线段叫做三角形的中线,三角形的三条中线相交于一点,这个点叫做三角形的重心.研究发现,三角形的重心把中线分成长度比为1:2的两部分,用数学语言表述为:如图1,在△ABC中,中线AD,CE相交于点G,则EG = $\frac{1}{2}CG$,DG = $\frac{1}{2}AG$.
证明:连接DE.
∵D,E分别是边BC,AB的中点,
∴____________________.
∴DE//AC,且DE = $\frac{1}{2}AC$.(依据)
∴∠DEC = ∠ACE,∠EDA = ∠DAC.
……

任务:
(1)材料中横线部分应填写的结论为____________________;材料中“依据”的定理内容是____________________.
(2)请将材料中的证明过程补充完整.
(3)如图2,在△MNH中,点K,L分别在边MN,MH上,连接HK,NL交于点F.若MK = $\frac{1}{3}MN$,ML = $\frac{1}{3}MH$,则KF与HF的数量关系为____________________.

答案:
12.解:
(1)DE是△ABC的中位线;三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
(2)证明过程补充如下:
∴△EDG∽△CAG,
∴$\frac{DE}{AC}$=$\frac{EG}{CG}$=$\frac{DG}{AG}$=$\frac{1}{2}$,
∴EG=$\frac{1}{2}$CG,DG=$\frac{1}{2}$AG.
(3)KF=$\frac{1}{3}$HF.
详解:如图,连接KL,

∵MK=$\frac{1}{3}$MN,ML=$\frac{1}{3}$MH,
∴$\frac{MK}{MN}$=$\frac{1}{3}$=$\frac{ML}{MH}$,
∵∠M = ∠M,
∴△MKL∽△MNH,
∴∠MKL = ∠MNH,$\frac{KL}{NH}$=$\frac{1}{3}$,
∴KL//NH,
∴∠FKL = ∠FHN,∠FLK = ∠FNH,
∴△KLF∽△HNF,
∴$\frac{KL}{NH}$=$\frac{KF}{HF}$=$\frac{1}{3}$,
∴KF = $\frac{1}{3}$HF.
12.解:
(1)DE是△ABC的中位线;三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
(2)证明过程补充如下:
∴△EDG∽△CAG,
∴$\frac{DE}{AC}$=$\frac{EG}{CG}$=$\frac{DG}{AG}$=$\frac{1}{2}$,
∴EG=$\frac{1}{2}$CG,DG=$\frac{1}{2}$AG.
(3)KF=$\frac{1}{3}$HF.
详解:如图,连接KL,

∵MK=$\frac{1}{3}$MN,ML=$\frac{1}{3}$MH,
∴$\frac{MK}{MN}$=$\frac{1}{3}$=$\frac{ML}{MH}$,
∵∠M = ∠M,
∴△MKL∽△MNH,
∴∠MKL = ∠MNH,$\frac{KL}{NH}$=$\frac{1}{3}$,
∴KL//NH,
∴∠FKL = ∠FHN,∠FLK = ∠FNH,
∴△KLF∽△HNF,
∴$\frac{KL}{NH}$=$\frac{KF}{HF}$=$\frac{1}{3}$,
∴KF = $\frac{1}{3}$HF.
查看更多完整答案,请扫码查看


