2025年53精准练九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
正弦:$\sin A = \frac{\angle A的\textcircled{1}\underline{对边}}{\text{斜边}}$
余弦:$\cos A = \frac{\angle A的\textcircled{2}\underline{邻边}}{\text{斜边}}$
正切:$\tan A = \frac{\textcircled{3}\underline{\angle A的对边}}{\textcircled{4}\underline{\angle A的邻边}}$
余弦:$\cos A = \frac{\angle A的\textcircled{2}\underline{邻边}}{\text{斜边}}$
正切:$\tan A = \frac{\textcircled{3}\underline{\angle A的对边}}{\textcircled{4}\underline{\angle A的邻边}}$
答案:
①对边 ②邻边 ③∠A的对边 ④∠A的邻边
$\sin 30^{\circ}=\textcircled{5}\underline{\ \ \ \ \ \ \ }$,$\cos 30^{\circ}=\textcircled{6}\underline{\ \ \ \ \ \ \ }$,$\tan 30^{\circ}=\textcircled{7}\underline{\ \ \ \ \ \ \ }$;
$\sin 45^{\circ}=\textcircled{8}\underline{\ \ \ \ \ \ \ }$,$\cos 45^{\circ}=\textcircled{9}\underline{\ \ \ \ \ \ \ }$,$\tan 45^{\circ}=\textcircled{10}\underline{\ \ \ \ \ \ \ }$;
$\sin 60^{\circ}=\textcircled{11}\underline{\ \ \ \ \ \ \ }$,$\cos 60^{\circ}=\textcircled{12}\underline{\ \ \ \ \ \ \ }$,$\tan 60^{\circ}=\textcircled{13}\underline{\ \ \ \ \ \ \ }$
$\sin 45^{\circ}=\textcircled{8}\underline{\ \ \ \ \ \ \ }$,$\cos 45^{\circ}=\textcircled{9}\underline{\ \ \ \ \ \ \ }$,$\tan 45^{\circ}=\textcircled{10}\underline{\ \ \ \ \ \ \ }$;
$\sin 60^{\circ}=\textcircled{11}\underline{\ \ \ \ \ \ \ }$,$\cos 60^{\circ}=\textcircled{12}\underline{\ \ \ \ \ \ \ }$,$\tan 60^{\circ}=\textcircled{13}\underline{\ \ \ \ \ \ \ }$
答案:
⑤$\frac{1}{2}$ ⑥$\frac{\sqrt{3}}{2}$ ⑦$\frac{\sqrt{3}}{3}$ ⑧$\frac{\sqrt{2}}{2}$ ⑨$\frac{\sqrt{2}}{2}$ ⑩1 ⑪$\frac{\sqrt{3}}{2}$ ⑫$\frac{1}{2}$ ⑬$\sqrt{3}$
$\sin45^{\circ}=\textcircled{8}\underline{\ \ \ \ \ \ \ }$,$\cos45^{\circ}=\textcircled{9}\underline{\ \ \ \ \ \ \ }$,$\tan45^{\circ}=\textcircled{10}\underline{\ \ \ \ \ \ \ }$;用科学计算器求
根据三角函数值求锐角的度数
根据三角函数值求锐角的度数
答案:
⑧$\frac{\sqrt{2}}{2}$ ⑨$\frac{\sqrt{2}}{2}$ ⑩1
1.[2023山西省实验中学月考]在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD \perp AB$,垂足为D,则下列式子中正确的是 ( )
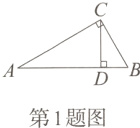
A. $\sin A = \frac{BC}{AB}$
B. $\tan A = \frac{BC}{AB}$
C. $\cos B = \frac{BD}{CD}$
D. $\tan B = \frac{CD}{BC}$

A. $\sin A = \frac{BC}{AB}$
B. $\tan A = \frac{BC}{AB}$
C. $\cos B = \frac{BD}{CD}$
D. $\tan B = \frac{CD}{BC}$
答案:
A
2.如图,在$5 \times 8$的正方形网格中,每个小正方形的边长均为1.若点A,B,C都在格点上,则$\sin B$的值为 ( )
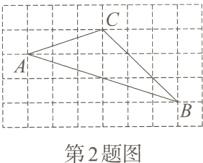
A. $\frac{\sqrt{5}}{2}$
B. $\frac{\sqrt{5}}{5}$
C. $\frac{\sqrt{10}}{5}$
D. $\frac{2\sqrt{5}}{5}$

A. $\frac{\sqrt{5}}{2}$
B. $\frac{\sqrt{5}}{5}$
C. $\frac{\sqrt{10}}{5}$
D. $\frac{2\sqrt{5}}{5}$
答案:
B
3.[2024运城一模改编]计算:$-2^{2}+\vert -3\vert+\sqrt{3}\sin 60^{\circ}-2^{-1} = \underline{\ \ \ \ \ \ \ }$.
答案:
0
4.在$\triangle ABC$中,$\angle A$、$\angle B$均为锐角,且满足$(2\sin^{2}A - 1)^{2}+\vert \tan(\angle B + 30^{\circ})-\sqrt{3}\vert = 0$,则$\angle C$的度数是$\underline{\ \ \ \ \ \ \ }$.
答案:
105°
5.[2024聊城三模]如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD$是中线,过点A作$CD$的垂线,分别交$BC$、$CD$于点E、F.若$\tan \angle CAE = \frac{2}{3}$,$AE = 26$,则$CD$的长为 ( )
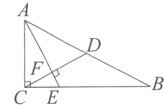
A. 39
B. $8\sqrt{13}$
C. $6\sqrt{13}$
D. 19.5

A. 39
B. $8\sqrt{13}$
C. $6\sqrt{13}$
D. 19.5
答案:
D
查看更多完整答案,请扫码查看


