2025年53精准练九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
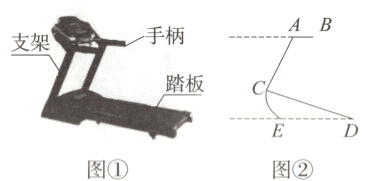
6. 图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄AB与地面DE平行,踏板CD的长为1.5 m,CD与地面DE的夹角∠CDE = α,支架AC的长为1 m,∠CAB = 120°,则跑步机手柄AB所在直线与地面DE之间的距离(单位:m)为 ( )
(
A. √3/2 + 1.5sin α
B. 1/2 + 1.5sin α
C. √3/2 + 1.5cos α
D. 1/2 + 1.5cos α
(

A. √3/2 + 1.5sin α
B. 1/2 + 1.5sin α
C. √3/2 + 1.5cos α
D. 1/2 + 1.5cos α
答案:
A
7.[2024晋中介休市期中改编]图1是小强在健身器材上进行仰卧起坐时的情景,图2是小强锻炼时上半身由ON位置运动到与地面CD垂直的OM位置时的示意图,已知ON = 0.7米,∠α = 30°,则M、N两点间的距离是多少米? (结果精确到0.1米,参考数据:√3≈1.73, √2≈1.41)


答案:
解:如图,过点N作NF⊥MO,交MO的延长线于点F.
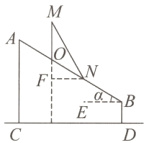
由题意得,OM = ON = 0.7米,NF//BE,
∴∠ANF = ∠ABE = ∠α = 30°.
在Rt△ONF中,
∠FON = 90° - ∠ANF = 60°,
FN = ON·cos 30° = $\frac{7\sqrt{3}}{20}$米.
∵∠FON是△MON的一个外角
∴∠FON = ∠OMN + ∠ONM,
∵OM = ON,
∴∠OMN = ∠ONM = $\frac{1}{2}$∠FON = 30°.

在Rt△MFN中,MN = FN÷sin 30° = $\frac{7\sqrt{3}}{10}$≈0.7×1.73≈1.2(米),
∴M、N两点间的距离约为1.2米.
解:如图,过点N作NF⊥MO,交MO的延长线于点F.

由题意得,OM = ON = 0.7米,NF//BE,
∴∠ANF = ∠ABE = ∠α = 30°.
在Rt△ONF中,
∠FON = 90° - ∠ANF = 60°,
FN = ON·cos 30° = $\frac{7\sqrt{3}}{20}$米.
∵∠FON是△MON的一个外角
∴∠FON = ∠OMN + ∠ONM,
∵OM = ON,
∴∠OMN = ∠ONM = $\frac{1}{2}$∠FON = 30°.

在Rt△MFN中,MN = FN÷sin 30° = $\frac{7\sqrt{3}}{10}$≈0.7×1.73≈1.2(米),
∴M、N两点间的距离约为1.2米.
8.[2024山西]研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动. 同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的3D扫描仪采集纪念碑的相关数据.
数据采集:如图,点A是纪念碑顶部一点,AB的长表示点A到水平地面的距离. 航模从纪念碑前水平地面的点M处竖直上升,飞行至距离地面20米的点C处时,测得点A的仰角∠ACD = 18.4°;然后沿CN方向继续飞行,飞行方向与水平线的夹角∠NCD = 37°,当到达点A正上方的点E处时,测得AE = 9米;……
数据应用:已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上. 请根据上述数据,计算纪念碑顶部点A到地面的距离(AB的长).(结果精确到1米;参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 18.4°≈0.32, cos 18.4°≈0.95,tan 18.4°≈0.33)
E.丶−N 、、|A
 C∠LD.''.
C∠LD.''.
1 B
数据采集:如图,点A是纪念碑顶部一点,AB的长表示点A到水平地面的距离. 航模从纪念碑前水平地面的点M处竖直上升,飞行至距离地面20米的点C处时,测得点A的仰角∠ACD = 18.4°;然后沿CN方向继续飞行,飞行方向与水平线的夹角∠NCD = 37°,当到达点A正上方的点E处时,测得AE = 9米;……
数据应用:已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上. 请根据上述数据,计算纪念碑顶部点A到地面的距离(AB的长).(结果精确到1米;参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 18.4°≈0.32, cos 18.4°≈0.95,tan 18.4°≈0.33)
E.丶−N 、、|A
 C∠LD.''.
C∠LD.''.1 B
答案:
解:如图,延长CD交AB于点H.
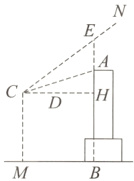
由题意得,四边形CMBH为矩形,
∴CM = HB = 20.
在Rt△ACH中,∠AHC = 90°,
∠ACH = 18.4°,
tan∠ACH = $\frac{AH}{CH}$,
∴CH = $\frac{AH}{tan∠ACH}$ = $\frac{AH}{tan 18.4°}$≈$\frac{AH}{0.33}$.
在Rt△ECH中,∠EHC = 90°,
∠ECH = 37°,
tan∠ECH = $\frac{EH}{CH}$,
∴CH = $\frac{EH}{tan∠ECH}$ = $\frac{EH}{tan 37°}$≈$\frac{EH}{0.75}$.
设AH = x,则EH = AH + AE = x + 9,
可得$\frac{x}{0.33}$ = $\frac{x + 9}{0.75}$,
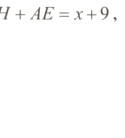
解得x≈7.1,
∴AB = AH + HB = 7.1 + 20 = 27.1≈27.
答:点A到地面的距离(AB的长)约为27米.
解:如图,延长CD交AB于点H.

由题意得,四边形CMBH为矩形,
∴CM = HB = 20.
在Rt△ACH中,∠AHC = 90°,
∠ACH = 18.4°,
tan∠ACH = $\frac{AH}{CH}$,
∴CH = $\frac{AH}{tan∠ACH}$ = $\frac{AH}{tan 18.4°}$≈$\frac{AH}{0.33}$.
在Rt△ECH中,∠EHC = 90°,
∠ECH = 37°,
tan∠ECH = $\frac{EH}{CH}$,
∴CH = $\frac{EH}{tan∠ECH}$ = $\frac{EH}{tan 37°}$≈$\frac{EH}{0.75}$.
设AH = x,则EH = AH + AE = x + 9,
可得$\frac{x}{0.33}$ = $\frac{x + 9}{0.75}$,
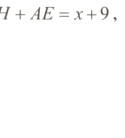
解得x≈7.1,
∴AB = AH + HB = 7.1 + 20 = 27.1≈27.
答:点A到地面的距离(AB的长)约为27米.
查看更多完整答案,请扫码查看


