《2025年53精准练九年级数学下册人教版山西专版》

1. 一次函数$y = kx + k(k\neq0)$与反比例函数$y = \frac{k}{x}$在同一平面直角坐标系中的大致图象是（ ）

答案： A

2. 在同一平面直角坐标系中，函数$y = mx + n$与$y = \frac{n}{mx}$(其中$m$，$n$是常数，$mn\neq0$)的大致图象可能是（ ）

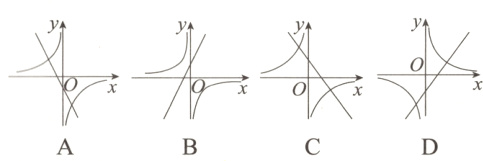
答案： C

3. 如图，一次函数$y = ax + b$与反比例函数$y = \frac{k}{x}(k ＞ 0)$的图象交于点$A(1,2)$，$B(m,-1)$，则$ax + b ＞ \frac{k}{x}$的解集是（ ）

A. $x ＜ -2$或$0 ＜ x ＜ 1$
B. $x ＜ -1$或$0 ＜ x ＜ 2$
C. $-2 ＜ x ＜ 0$或$x ＞ 1$
D. $-1 ＜ x ＜ 0$或$x ＞ 2$

答案： C

4. [2023怀化]如图，反比例函数$y = \frac{k}{x}(k ＞ 0)$的图象与过点$(-1,0)$的直线$AB$相交于$A$、$B$两点.已知点$A$的坐标为$(1,3)$，点$C$为$x$轴上任意一点.如果$S_{\triangle ABC} = 9$，那么点$C$的坐标为（ ）

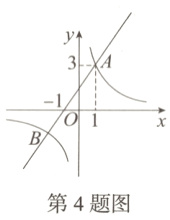
A. $(-3,0)$
B. $(5,0)$
C. $(-3,0)$或$(5,0)$
D. $(3,0)$或$(-5,0)$

答案： D

5. 如图，一次函数$y = ax + b$的图象与反比例函数$y = \frac{k}{x}$的图象在第一象限内交于点$A$、$B$，与$x$轴交于点$C$，$AB = BC$.若$\triangle OAC$的面积为8，则$k$的值为（ ）

A. 2
B. $\frac{8}{3}$
C. $\frac{16}{3}$
D. 4

答案： C

6. [2024太原三模]如图，一次函数$y = \frac{1}{2}x - 1$的图象与反比例函数$y = \frac{k}{x}(k\neq0)$的图象相交于点$A(m,2)$和点$B$，与$y$轴交于点$C$.
(1)求反比例函数的解析式；
(2)点$P$是$y$轴上的一个动点，且$\triangle ACP$是以$AC$为腰的等腰三角形，请直接写出点$P$的坐标.

答案： 解:
(1)
∵点A(m,2)在一次函数y = $\frac{1}{2}$x−1的图象上，
∴$\frac{1}{2}$m−1=2,
解得m=6,
∴A(6,2),
∵A(6,2)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上，
∴2=$\frac{k}{6}$,
解得k=12,
∴反比例函数的解析式为y=$\frac{12}{x}$.
(2)点P的坐标为(0,3$\sqrt{5}$−1)或(0, -3$\sqrt{5}$−1)或(0,5).
详解:
∵直线AB的解析式为y=$\frac{1}{2}$x−1,
∴当x=0时,y=−1,
∴C(0,−1),
∵A(6,2),
∴AC=$\sqrt{(6 - 0)^2+(2 + 1)^2}=\sqrt{36 + 9}=\sqrt{45}=3\sqrt{5}$.
当AC=PC时,设P(0,y),
则|y + 1| = 3$\sqrt{5}$,
解得y=3$\sqrt{5}$−1或y=−3$\sqrt{5}$−1,
∴P1(0,3$\sqrt{5}$−1),P2(0,−3$\sqrt{5}$−1);
当AC=AP时,过点A作AD⊥y轴于点D,则CD=3,
∴PD=CD=3,
∴P3(0,5).
综上所述，点P的坐标为(0,3$\sqrt{5}$−1)或(0,−3$\sqrt{5}$−1)或(0,5).