《2025年53精准练九年级数学下册人教版山西专版》

1.[2023运城盐湖区期中]已知反比例函数的图象经过点(2, -4)，那么这个反比例函数的解析式是（ ）
A. $y=\frac{2}{x}$
B. $y=-\frac{2}{x}$
C. $y=\frac{8}{x}$
D. $y=-\frac{8}{x}$

答案： D

2.[2024吕梁中阳县期末]已知A(-6, 2)，B(n, -4)是反比例函数$y=\frac{k}{x}$的图象上的两点，求反比例函数的解析式及n的值。

答案： 解：
∵点$A(-6,2)$在反比例函数$y=\frac{k}{x}$的图象上，
$\therefore k = xy = -6\times2 = -12$，
$\therefore$反比例函数的解析式为$y = -\frac{12}{x}$.
$\because$点$B(n,-4)$在反比例函数$y = -\frac{12}{x}$的图象上，
$\therefore -4 = -\frac{12}{n}$，
$\therefore n = 3$.

3.如图，点A在反比例函数$y=\frac{k}{x}(x ＞ 0)$的图象上，若矩形ABOC的面积为3，则k的值为( )

A. $-\frac{3}{2}$
B. $\frac{3}{2}$
C. -3
D. 3

答案： D

4.反比例函数$y=\frac{k}{x}(x ＜ 0)$的图象如图所示，AB//y轴，△ABC的面积为3，则k的值为( )

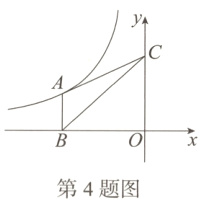
A. $\frac{1}{2}$
B. $-\frac{3}{2}$
C. 3
D. -6

答案： D

5.如图，反比例函数$y_1=\frac{4}{x}$和$y_2=\frac{2}{x}$在第一象限内的图象分别是C1和C2，设点P在C1上，PA⊥x轴于点A，交C2于点B，则△POB的面积为( )

A. 4
B. 2
C. 1
D. 6

答案： C

6.已知反比例函数$y=\frac{k - 3}{x}$(k为常数)与正比例函数y = x的图象有交点，则k的取值范围是（ ）
A. k ＞ 0
B. k ＜ 0
C. k ＞ 3
D. k ＜ 3

答案： C

7.[2024晋城期中]如图，在平面直角坐标系中，一次函数y = k1x + b的图象与反比例函数$y=\frac{k_2}{x}$的图象交于A(4, -2)，B(-2, n)两点。
(1)求反比例函数和一次函数的表达式；
(2)连接OA，OB，求△ABO的面积；
(3)不等式$k_1x + b＞\frac{k_2}{x}$的解集是____________________。

答案： 解：
(1) $\because A(4,-2)$在反比例函数$y = \frac{k_2}{x}$的图象上，
$\therefore k_2 = xy = 4\times(-2) = -8$，
$\therefore$反比例函数的表达式为$y = -\frac{8}{x}$.
$\because B(-2,n)$在反比例函数$y = -\frac{8}{x}$的图象上，
$\therefore n = -\frac{8}{-2} = 4$，即$B$的坐标为$(-2,4)$.
将$A$，$B$两点坐标代入$y = k_1x + b$中，
得$\begin{cases}4k_1 + b = -2,\\-2k_1 + b = 4,\end{cases}$
$\therefore\begin{cases}k_1 = -1,\\b = 2,\end{cases}$
$\therefore$一次函数的表达式为$y = -x + 2$.
(2) 如图所示，设一次函数的图象与$x$轴交于点$C$，
对于一次函数$y = -x + 2$，令$y = 0$，得$x = 2$，即$OC = 2$，
$\therefore S_{\triangle AOB} = S_{\triangle AOC} + S_{\triangle BOC} = \frac{1}{2}\times2\times2 + \frac{1}{2}\times2\times4 = 6$.
(3) $x ＜ -2$或$0 ＜ x ＜ 4$.