2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第96页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
18.(17分)已知函数f(x)=ln$\frac{x}{2−x}$+ax+b(x−1)³.
(1)若b=0,且f'(x)≥0,求a的最小值;
(2)证明:曲线y=f(x)是中心对称图形;
(3)若f(x)>−2当且仅当1<x<2,求b的取值范围.
答案:
18.[命题点]导数的运算、不等式恒成立求参数范围
(1)[解]当b=0时,f(x)=ln$\frac{x}{2−x}$+ax,x∈(0,2),
则f'(x)=$\frac{2−x}{x}$.$\frac{x}{2−x}$)+a=$\frac{2−x}{x}$.$\frac{2−x−(−1)x}{(2−x)²}$+a=$\frac{2}{x(2−x)}$+a.
2分
∵f'(x)≥0,
∴a≥$\frac{2}{x(x−2)}$在(0,2)上恒成立.
当x∈(0,2)时,x(x−2)∈[−1,0),
∴$\frac{2}{x(x−2)}$∈(−∞o,−2],
∴a∈[−2,+8),即a的最小值为−2. 5分
(2)[证明]
∵∮(x)=In$\frac{x}{2−x}$+ax+b(x−1)²,x∈(0,2),
∴∮(x+1)=1n↓1−+xax+a+bx²,x∈(−1,1). 6分令g(x)=J(x+1)−a=ln$\frac{1+x}{1−x}$+ax+bx²,x∈(−1,1),则g(−x)=
ln$\frac{1−x}{1+x}$−ax−bx²=−ln$\frac{1+x}{1−x}$−ax−bx²=−g(x),
∴g(x)是定义域为(−1,1)的奇函数,其图像关于坐标原点0对称. 9分又
∵∮(x)的图像可由g(x)的图像向右平移1个单位长度,再向上平移a个单位长度得到,
∴曲线y=f(x)是中心对称图形.
10分一题多解∮(x)的定义域为(0,2)f
(1)=a.6分当x∈(−1,1)时,f(1+x)=ln$\frac{1+x}{1−x}$+a(1+x)+bx²,f(1−x)=
ln$\frac{1−x}{1+x}$+a(1−x)−bx²,
∴∮(1+x)+∮(1−x)=ln$\frac{1+x}{1−x}$+ln$\frac{1−x}{1+x}$+2a=2a,
∴曲线y=f(x)关于点(1,a)中心对称,即曲线y=f(x)是中心对称图形.
10分
(3)[解]
∵∮(x)>−2当且仅当1<x<2,
∴∮
(1)=−2=>a=−2,
∴∮(x)=ln$\frac{x}{2−x}$2x+b(x−1)²>−2对任意x∈(1,2)恒成立,∮'(x)=$\frac{1}{x}$+$\frac{1}{2−x}$−2+3b(x−1)²=$\frac{2(x−1)}{x(2−x)}$+3b(x−1)²=(x−1)²².
[x(22−x)3b]. 12分令m(x)=x(22|x)+3b,
∴必有m
(1)=2+3b≥0=b≥−$\frac{2}{3}$.
否则若b<−$\frac{2}{3}$,则存在δ(1<δ<2)使得当x∈(1,δ)时f'(x)<0,f(x)在(1,δ)上单调递减,
∴∮(δ)<f
(1)=−2. 13分当b≥−$\frac{2}{3}$时,对任意x∈(1,2)∮(x)≥ln$\frac{x}{2−x}$−2x−$\frac{2}{3}$(x−1)²,令h(x)=1n$\frac{x}{2−x}$−2x−$\frac{2}{3}$(x−1)²,则h'(x)=$\frac{2(x−1)}{x(2−x)}$−2(x−1)²=
2(x−1)²[$\frac{1}{x(2−x)}$−1]>0,对任意x∈(1,2)恒成立"
∴h(x)>h
(1)=−2,符合条件. 16分综上可得b的取值范围是[−+∞) 17分
(1)[解]当b=0时,f(x)=ln$\frac{x}{2−x}$+ax,x∈(0,2),
则f'(x)=$\frac{2−x}{x}$.$\frac{x}{2−x}$)+a=$\frac{2−x}{x}$.$\frac{2−x−(−1)x}{(2−x)²}$+a=$\frac{2}{x(2−x)}$+a.
2分
∵f'(x)≥0,
∴a≥$\frac{2}{x(x−2)}$在(0,2)上恒成立.
当x∈(0,2)时,x(x−2)∈[−1,0),
∴$\frac{2}{x(x−2)}$∈(−∞o,−2],
∴a∈[−2,+8),即a的最小值为−2. 5分
(2)[证明]
∵∮(x)=In$\frac{x}{2−x}$+ax+b(x−1)²,x∈(0,2),
∴∮(x+1)=1n↓1−+xax+a+bx²,x∈(−1,1). 6分令g(x)=J(x+1)−a=ln$\frac{1+x}{1−x}$+ax+bx²,x∈(−1,1),则g(−x)=
ln$\frac{1−x}{1+x}$−ax−bx²=−ln$\frac{1+x}{1−x}$−ax−bx²=−g(x),
∴g(x)是定义域为(−1,1)的奇函数,其图像关于坐标原点0对称. 9分又
∵∮(x)的图像可由g(x)的图像向右平移1个单位长度,再向上平移a个单位长度得到,
∴曲线y=f(x)是中心对称图形.
10分一题多解∮(x)的定义域为(0,2)f
(1)=a.6分当x∈(−1,1)时,f(1+x)=ln$\frac{1+x}{1−x}$+a(1+x)+bx²,f(1−x)=
ln$\frac{1−x}{1+x}$+a(1−x)−bx²,
∴∮(1+x)+∮(1−x)=ln$\frac{1+x}{1−x}$+ln$\frac{1−x}{1+x}$+2a=2a,
∴曲线y=f(x)关于点(1,a)中心对称,即曲线y=f(x)是中心对称图形.
10分
(3)[解]
∵∮(x)>−2当且仅当1<x<2,
∴∮
(1)=−2=>a=−2,
∴∮(x)=ln$\frac{x}{2−x}$2x+b(x−1)²>−2对任意x∈(1,2)恒成立,∮'(x)=$\frac{1}{x}$+$\frac{1}{2−x}$−2+3b(x−1)²=$\frac{2(x−1)}{x(2−x)}$+3b(x−1)²=(x−1)²².
[x(22−x)3b]. 12分令m(x)=x(22|x)+3b,
∴必有m
(1)=2+3b≥0=b≥−$\frac{2}{3}$.
否则若b<−$\frac{2}{3}$,则存在δ(1<δ<2)使得当x∈(1,δ)时f'(x)<0,f(x)在(1,δ)上单调递减,
∴∮(δ)<f
(1)=−2. 13分当b≥−$\frac{2}{3}$时,对任意x∈(1,2)∮(x)≥ln$\frac{x}{2−x}$−2x−$\frac{2}{3}$(x−1)²,令h(x)=1n$\frac{x}{2−x}$−2x−$\frac{2}{3}$(x−1)²,则h'(x)=$\frac{2(x−1)}{x(2−x)}$−2(x−1)²=
2(x−1)²[$\frac{1}{x(2−x)}$−1]>0,对任意x∈(1,2)恒成立"
∴h(x)>h
(1)=−2,符合条件. 16分综上可得b的取值范围是[−+∞) 17分
19. (17分)设m为正整数,数列$a_1,a_2,\cdots,a_{4m + 2}$是公差不为0的等差数列,若从中删去两项$a_i$和$a_j$($i<j$)后剩余的4m项可被平均分为m组,且每组的4个数都能构成等差数列,则称数列$a_1,a_2,\cdots,a_{4m + 2}$是$(i,j)$−可分数列。
(1)写出所有的$(i,j)$,$1\leq i<j\leq6$,使得数列$a_1,a_2,\cdots,a_6$是$(i,j)$−可分数列;
(2)当$m\geq3$时,证明:数列$a_1,a_2,\cdots,a_{4m + 2}$是$(2,13)$−可分数列;
(3)从1,2,$\cdots$,4m + 2中一次任取两个数i和j($i<j$),记数列$a_1,a_2,\cdots,a_{4m + 2}$是$(i,j)$−可分数列的概率为$P_m$,证明:$P_m>\frac{1}{8}$。
(1)写出所有的$(i,j)$,$1\leq i<j\leq6$,使得数列$a_1,a_2,\cdots,a_6$是$(i,j)$−可分数列;
(2)当$m\geq3$时,证明:数列$a_1,a_2,\cdots,a_{4m + 2}$是$(2,13)$−可分数列;
(3)从1,2,$\cdots$,4m + 2中一次任取两个数i和j($i<j$),记数列$a_1,a_2,\cdots,a_{4m + 2}$是$(i,j)$−可分数列的概率为$P_m$,证明:$P_m>\frac{1}{8}$。
答案:
19.[命题点]数列新定义
(1)[解]满足题意的(i,j)为(1,2),(1,6),(5,6). 3分
(2)[证明]因为在公差不为0的等差数列{an}中,ap,aq,am,an成等差数列,则p,q,m,n成等差数列. 5分
当m≥3时,a1,a2,…,a4m + 2可连续4项为一组构成等差数列.
故需证明序号为1,3,4,5,6,7,8,9,10,11,12,14的项可分成三组项数为4的等差数列,易知分为(1,4,7,10),(3,6,9,12),(5,8,11,14)三组满足题意,所以当m≥3时,数列a1,a2,…,a4m + 2是(2,13)−可分数列. 7分
(3)[证明]解法一:由
(2)可知,等差数列a1,a2,…,a4m + 2是(i,j)−可分数列⇔数列1,2,…,4m + 2是(i,j)−可分数列.
下面证明1,2,…,4m + 2是(4k + 1,4r + 2)−可分数列(0≤k≤r≤m).
当r = k时,4k + 1与4r + 2是相邻两项,可分为(1,2,3,4),(5,6,7,8),…,(4k - 3,4k - 2,4k - 1,4k),(4k + 3,4k + 4,4k + 5,4k + 6),…,(4m - 1,4m,4m + 1,4m + 2). 9分
当r>k时,4k + 1,4k + 2,…,4r + 1,4r + 2,共4(r - k) + 2项,中间的4(r - k)项可连续4项为一组,前后的项可分为(1,2,3,4),…,(4k - 3,4k - 2,4k - 1,4k)与(4(r + 1) - 1,4(r + 1),4(r + 1) + 1,4(r + 1) + 2),…,(4m - 1,4m,4m + 1,4m + 2).
此时,(k,r)共有$C_{m + 1}^2=\frac{1}{2}(m + 1)(m + 2)$组. 10分
再证:1,2,…,4m + 2是(4k + 2,4r + 1)−可分数列(0≤k<r≤m).
易知1~4k与4r + 3~4m + 2是可分的,只需考虑4k + 1,4k + 3,4k + 4,…,4r - 1,4r,4r + 2的可分性.
设p = r - k∈N*,只需证:1,3,4,…,4p - 1,4p,4p + 2可分(提示:1~4p + 2去掉2与4p + 1).
当p = 1时,1,3,4,6,无法做到;
当p = 2时,1,3, ,可以做到;
,可以做到;
当p = 3时,1,3,4,5,6,7,8,9,10,11,12,可以做到;
当p = 4时,1,3,4,5,6,7,8,9,10,11,12,13,14,15,16,18,(1,5,9,13),(3,7,11,15),(4,8,12,16),(6,10,14,18)满足题意. 13分
故∀p≥2,可划分为:(1,p + 1,2p + 1,3p + 1),(3,p + 3,2p + 3,3p + 3),(4,p + 4,2p + 4,3p + 4),(5,p + 5,2p + 5,3p + 5),…,(p,2p,3p,4p),(p + 2,2p + 2,3p + 2,4p + 2),共p组.
事实上,就是(i,p + i,2p + i,3p + i),i = 1,3,…,p,p + 2,且把2换成4k + 2,此时,(k,r)即(k,k + p),p≥2共有$C_{m}^2 - m=\frac{1}{2}m(m - 1)$组.(提示:(0,1),(1,2),…,(m - 1,m)不可行)
综上,可行的(4k + 2,4r + 1)与(4k + 1,4r + 2)至少有$\frac{1}{2}m(m - 1)+\frac{1}{2}(m + 1)(m + 2)$组. 16分
故$P_m\geq\frac{\frac{1}{2}(2m^2 + 2m + 2)}{C_{4m + 2}^2}=\frac{m^2 + m + 1}{(2m + 1)(4m + 1)}=\frac{m^2 + m + 1}{8m^2 + 6m + 1}>\frac{1}{8}$,得证! 17分
解法二:对于等差数列a1,a2,…,a4m + 2中的ai,aj,i<j
若i≡1(mod 4),j≡2(mod 4),则
a1,a2,a3,a4;a5,a6,a7,a8;…;ai - 4,ai - 3,ai - 2,ai - 1构成$\frac{i - 1}{4}$个等差数列,
ai + 1,ai + 2,ai + 3,ai + 4;ai + 5,ai + 6,ai + 7,ai + 8;…;aj - 4,aj - 3,aj - 2,aj - 1构成$\frac{j - i}{4}-1$个等差数列,
aj + 1,aj + 2,aj + 3,aj + 4;aj + 5,aj + 6,aj + 7,aj + 8;…;a4m - 1,a4m,a4m + 1,a4m + 2构成$\frac{4m + 2 - j}{4}$个等差数列,
故成立. 10分
此时,(i,j)有$C_{m + 1}^2=\frac{1}{2}(m + 1)(m + 2)$组,
$\frac{\frac{1}{2}(m + 1)(m + 2)}{C_{4m + 2}^2}=\frac{m^2 + 3m + 2}{16m^2 + 12m + 2}>\frac{1}{16}$
由
(2)可知,考虑i<j,i≡2(mod 4),j≡1(mod 4)的可行性.
令k = $\frac{1 - i}{4}$,则k∈N*.
当k = 1时,有1,3,4,6,不可行.
当k = 2时,有(1,3,5,7),(4,6,8,10).
当k = 3时,有(1,4,7,10),(3,6,9,12),(5,8,11,14).
不难发现几个等差数列的公差均为k,故我们可尝试构造一个关于k的一般性的式子求解. 13分
对于i = 4p + 2,j = 4q + 1的情况:a1,a2,a3,a4;a5,a6,a7,a8;…;ai - 3,ai - 2,ai - 1构成$\frac{i - 2}{4}$个等差数列
而对于中间部分,不妨i = 2,j = 4k + 1.
则(1,1 + k,1 + 2k,1 + 3k),(3,3 + k,3 + 2k,3 + 3k),(4,4 + k,4 + 2k,4 + 3k),…,(k - 1,2k - 1,3k - 1,4k - 1),(k,2k,3k,4k),(k + 2,2k + 2,3k + 2,4k + 2),此时恰好没有2和4k + 1,恰好是k个等差数列,故构造成立. 15分
综上,已证i<j,i≡1(mod 4),j≡2(mod 4)时成立;i<j,i≡2(mod 4),j≡1(mod 4)且j≠i + 3时成立.
首先:$C_{4m + 2}^2=(2m + 1)(4m + 1)$,
1°当i = 1时,有m + 1个j满足;当i = 5时,有m个j满足;…;当i = 4m + 1时,有1个j满足
共有$\frac{(m + 1)(m + 2)}{2}$组(i,j).
2°当i = 2时,有m - 1个j满足;当i = 6时,有m - 2个j满足;…;当i = 4m - 2时,有0个j满足
共有$\frac{(m - 1)m}{2}$组(i,j).
故$P_m\geq\frac{\frac{(m - 1)m}{2}+\frac{(m + 2)(m + 1)}{2}}{(2m + 1)(4m + 1)}=\frac{m^2 + m + 1}{8m^2 + 6m + 1}>\frac{1}{8}$,证毕. 17分
解法三:先证数列a1,a2,…,a4m + 2是(2,4k + 1)(其中k≥2)−可分数列
当k = 2时,a1,a3,a4,a5,a6,a7,a8,a9分成(a1,a3,a5,a7),(a4,a6,a8,a9)两组等差数列,a1,a2,…,a4m + 2,4项一组成等差数列,所以k = 2时成立.
当k = 3时,由
(2)可知数列是(2,13)−可分数列.
当k = 4时,a1,a2,…,a16,a18分成(a1,a5,a9,a13),(a3,a7,a11,a15),(a4,a8,a12,a16),(a6,a10,a14,a18)四组等差数列,a19,a20,a21,a22,…,a4m + 2,4项一组成等差数列,所以k = 4成立.
以此类推,当k = m时,a1,…,a4m + 2可划分成(a1,a1 + m,a1 + 2m,a1 + 3m),(a3,a3 + m,a3 + 2m,a3 + 3m),…,(am,a2m,a3m,a4m),(a2 + m,a2 + 2m,a2 + 3m,a2 + 4m),共m组等差数列. 12分
下面用数学归纳法证明$P_m>\frac{1}{8}$.
①当m = 1时,删去的(ai,aj)为(a1,a6),(a1,a2),(a5,a6),共3个,$P_1=\frac{3}{C_{6}^2}=\frac{3}{15}=\frac{1}{5}>\frac{1}{8}$,
∴$P_m>\frac{1}{8}$成立.
②假设m = k(k≥1)时,$P_m>\frac{1}{8}$成立,则当m = k + 1时,
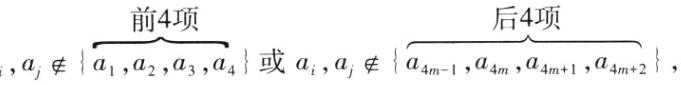
1°若ai,aj∈{a5,a6,…,a4k + 2},则去掉这4项,变为m = k的情形;
2°若ai∈{a1,a2,a3,a4},aj∈{a4m - 1,a4m,a4m + 1,a4m + 2},(ai,aj)共4×4 = 16种情况,其中(ai,a4m + 2)和(a2,a4m + 1)成立,至少两种;
当ai,aj∈{a1,a2,a3,a4}或ai,aj∈{a4m - 1,a4m,a4m + 1,a4m + 2},其中(a1,a2)和(a4m + 1,a4m + 2)成立,概率为$\frac{1}{C_{4}^2}=\frac{1}{6}$
所以$P_{k + 1}>P(1°)\cdot P_k+P(2°)\cdot\frac{2}{16}$.
又因为P(1°)+P(2°)=1,所以$P_{k + 1}>P(1°)\cdot\frac{1}{8}+(1 - P(1°))\cdot\frac{1}{8}=\frac{1}{8}$
由①②可知,$P_m>\frac{1}{8}$对m∈N*恒成立,所以$P_m>\frac{1}{8}$成立.得证! 17分
19.[命题点]数列新定义
(1)[解]满足题意的(i,j)为(1,2),(1,6),(5,6). 3分
(2)[证明]因为在公差不为0的等差数列{an}中,ap,aq,am,an成等差数列,则p,q,m,n成等差数列. 5分
当m≥3时,a1,a2,…,a4m + 2可连续4项为一组构成等差数列.
故需证明序号为1,3,4,5,6,7,8,9,10,11,12,14的项可分成三组项数为4的等差数列,易知分为(1,4,7,10),(3,6,9,12),(5,8,11,14)三组满足题意,所以当m≥3时,数列a1,a2,…,a4m + 2是(2,13)−可分数列. 7分
(3)[证明]解法一:由
(2)可知,等差数列a1,a2,…,a4m + 2是(i,j)−可分数列⇔数列1,2,…,4m + 2是(i,j)−可分数列.
下面证明1,2,…,4m + 2是(4k + 1,4r + 2)−可分数列(0≤k≤r≤m).
当r = k时,4k + 1与4r + 2是相邻两项,可分为(1,2,3,4),(5,6,7,8),…,(4k - 3,4k - 2,4k - 1,4k),(4k + 3,4k + 4,4k + 5,4k + 6),…,(4m - 1,4m,4m + 1,4m + 2). 9分
当r>k时,4k + 1,4k + 2,…,4r + 1,4r + 2,共4(r - k) + 2项,中间的4(r - k)项可连续4项为一组,前后的项可分为(1,2,3,4),…,(4k - 3,4k - 2,4k - 1,4k)与(4(r + 1) - 1,4(r + 1),4(r + 1) + 1,4(r + 1) + 2),…,(4m - 1,4m,4m + 1,4m + 2).
此时,(k,r)共有$C_{m + 1}^2=\frac{1}{2}(m + 1)(m + 2)$组. 10分
再证:1,2,…,4m + 2是(4k + 2,4r + 1)−可分数列(0≤k<r≤m).
易知1~4k与4r + 3~4m + 2是可分的,只需考虑4k + 1,4k + 3,4k + 4,…,4r - 1,4r,4r + 2的可分性.
设p = r - k∈N*,只需证:1,3,4,…,4p - 1,4p,4p + 2可分(提示:1~4p + 2去掉2与4p + 1).
当p = 1时,1,3,4,6,无法做到;
当p = 2时,1,3,
 ,可以做到;
,可以做到;当p = 3时,1,3,4,5,6,7,8,9,10,11,12,可以做到;
当p = 4时,1,3,4,5,6,7,8,9,10,11,12,13,14,15,16,18,(1,5,9,13),(3,7,11,15),(4,8,12,16),(6,10,14,18)满足题意. 13分
故∀p≥2,可划分为:(1,p + 1,2p + 1,3p + 1),(3,p + 3,2p + 3,3p + 3),(4,p + 4,2p + 4,3p + 4),(5,p + 5,2p + 5,3p + 5),…,(p,2p,3p,4p),(p + 2,2p + 2,3p + 2,4p + 2),共p组.
事实上,就是(i,p + i,2p + i,3p + i),i = 1,3,…,p,p + 2,且把2换成4k + 2,此时,(k,r)即(k,k + p),p≥2共有$C_{m}^2 - m=\frac{1}{2}m(m - 1)$组.(提示:(0,1),(1,2),…,(m - 1,m)不可行)
综上,可行的(4k + 2,4r + 1)与(4k + 1,4r + 2)至少有$\frac{1}{2}m(m - 1)+\frac{1}{2}(m + 1)(m + 2)$组. 16分
故$P_m\geq\frac{\frac{1}{2}(2m^2 + 2m + 2)}{C_{4m + 2}^2}=\frac{m^2 + m + 1}{(2m + 1)(4m + 1)}=\frac{m^2 + m + 1}{8m^2 + 6m + 1}>\frac{1}{8}$,得证! 17分
解法二:对于等差数列a1,a2,…,a4m + 2中的ai,aj,i<j
若i≡1(mod 4),j≡2(mod 4),则
a1,a2,a3,a4;a5,a6,a7,a8;…;ai - 4,ai - 3,ai - 2,ai - 1构成$\frac{i - 1}{4}$个等差数列,
ai + 1,ai + 2,ai + 3,ai + 4;ai + 5,ai + 6,ai + 7,ai + 8;…;aj - 4,aj - 3,aj - 2,aj - 1构成$\frac{j - i}{4}-1$个等差数列,
aj + 1,aj + 2,aj + 3,aj + 4;aj + 5,aj + 6,aj + 7,aj + 8;…;a4m - 1,a4m,a4m + 1,a4m + 2构成$\frac{4m + 2 - j}{4}$个等差数列,
故成立. 10分
此时,(i,j)有$C_{m + 1}^2=\frac{1}{2}(m + 1)(m + 2)$组,
$\frac{\frac{1}{2}(m + 1)(m + 2)}{C_{4m + 2}^2}=\frac{m^2 + 3m + 2}{16m^2 + 12m + 2}>\frac{1}{16}$
由
(2)可知,考虑i<j,i≡2(mod 4),j≡1(mod 4)的可行性.
令k = $\frac{1 - i}{4}$,则k∈N*.
当k = 1时,有1,3,4,6,不可行.
当k = 2时,有(1,3,5,7),(4,6,8,10).
当k = 3时,有(1,4,7,10),(3,6,9,12),(5,8,11,14).
不难发现几个等差数列的公差均为k,故我们可尝试构造一个关于k的一般性的式子求解. 13分
对于i = 4p + 2,j = 4q + 1的情况:a1,a2,a3,a4;a5,a6,a7,a8;…;ai - 3,ai - 2,ai - 1构成$\frac{i - 2}{4}$个等差数列
而对于中间部分,不妨i = 2,j = 4k + 1.
则(1,1 + k,1 + 2k,1 + 3k),(3,3 + k,3 + 2k,3 + 3k),(4,4 + k,4 + 2k,4 + 3k),…,(k - 1,2k - 1,3k - 1,4k - 1),(k,2k,3k,4k),(k + 2,2k + 2,3k + 2,4k + 2),此时恰好没有2和4k + 1,恰好是k个等差数列,故构造成立. 15分
综上,已证i<j,i≡1(mod 4),j≡2(mod 4)时成立;i<j,i≡2(mod 4),j≡1(mod 4)且j≠i + 3时成立.
首先:$C_{4m + 2}^2=(2m + 1)(4m + 1)$,
1°当i = 1时,有m + 1个j满足;当i = 5时,有m个j满足;…;当i = 4m + 1时,有1个j满足
共有$\frac{(m + 1)(m + 2)}{2}$组(i,j).
2°当i = 2时,有m - 1个j满足;当i = 6时,有m - 2个j满足;…;当i = 4m - 2时,有0个j满足
共有$\frac{(m - 1)m}{2}$组(i,j).
故$P_m\geq\frac{\frac{(m - 1)m}{2}+\frac{(m + 2)(m + 1)}{2}}{(2m + 1)(4m + 1)}=\frac{m^2 + m + 1}{8m^2 + 6m + 1}>\frac{1}{8}$,证毕. 17分
解法三:先证数列a1,a2,…,a4m + 2是(2,4k + 1)(其中k≥2)−可分数列
当k = 2时,a1,a3,a4,a5,a6,a7,a8,a9分成(a1,a3,a5,a7),(a4,a6,a8,a9)两组等差数列,a1,a2,…,a4m + 2,4项一组成等差数列,所以k = 2时成立.
当k = 3时,由
(2)可知数列是(2,13)−可分数列.
当k = 4时,a1,a2,…,a16,a18分成(a1,a5,a9,a13),(a3,a7,a11,a15),(a4,a8,a12,a16),(a6,a10,a14,a18)四组等差数列,a19,a20,a21,a22,…,a4m + 2,4项一组成等差数列,所以k = 4成立.
以此类推,当k = m时,a1,…,a4m + 2可划分成(a1,a1 + m,a1 + 2m,a1 + 3m),(a3,a3 + m,a3 + 2m,a3 + 3m),…,(am,a2m,a3m,a4m),(a2 + m,a2 + 2m,a2 + 3m,a2 + 4m),共m组等差数列. 12分
下面用数学归纳法证明$P_m>\frac{1}{8}$.
①当m = 1时,删去的(ai,aj)为(a1,a6),(a1,a2),(a5,a6),共3个,$P_1=\frac{3}{C_{6}^2}=\frac{3}{15}=\frac{1}{5}>\frac{1}{8}$,
∴$P_m>\frac{1}{8}$成立.
②假设m = k(k≥1)时,$P_m>\frac{1}{8}$成立,则当m = k + 1时,
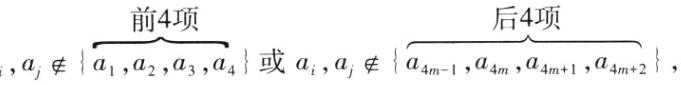
1°若ai,aj∈{a5,a6,…,a4k + 2},则去掉这4项,变为m = k的情形;
2°若ai∈{a1,a2,a3,a4},aj∈{a4m - 1,a4m,a4m + 1,a4m + 2},(ai,aj)共4×4 = 16种情况,其中(ai,a4m + 2)和(a2,a4m + 1)成立,至少两种;
当ai,aj∈{a1,a2,a3,a4}或ai,aj∈{a4m - 1,a4m,a4m + 1,a4m + 2},其中(a1,a2)和(a4m + 1,a4m + 2)成立,概率为$\frac{1}{C_{4}^2}=\frac{1}{6}$
所以$P_{k + 1}>P(1°)\cdot P_k+P(2°)\cdot\frac{2}{16}$.
又因为P(1°)+P(2°)=1,所以$P_{k + 1}>P(1°)\cdot\frac{1}{8}+(1 - P(1°))\cdot\frac{1}{8}=\frac{1}{8}$
由①②可知,$P_m>\frac{1}{8}$对m∈N*恒成立,所以$P_m>\frac{1}{8}$成立.得证! 17分
查看更多完整答案,请扫码查看


