2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1.已知集合A={(x,y)|x,y∈N,y≥x},B={(x,y)|x + y = 8},则A∩B中元素的个数为 ( )
A.2
B.3
C.4
D.6
A.2
B.3
C.4
D.6
答案:
1.C [命题点]集合的表示方法,集合的交集运算,集合中元素的个数
[深度解析]依题意A∩B的元素是直线x + y = 8上满足x, y∈N,且y≥x的点,即点(1, 7),(2, 6),(3, 5),(4, 4)。故选C。
[深度解析]依题意A∩B的元素是直线x + y = 8上满足x, y∈N,且y≥x的点,即点(1, 7),(2, 6),(3, 5),(4, 4)。故选C。
2.复数$\frac{1}{1−3i}$的虚部是 ( )
A.−$\frac{3}{10}$
B.−$\frac{1}{10}$
C.$\frac{1}{10}$
D.$\frac{3}{10}$
A.−$\frac{3}{10}$
B.−$\frac{1}{10}$
C.$\frac{1}{10}$
D.$\frac{3}{10}$
答案:
2.D [命题点]复数的概念及乘除运算
[深度解析]因为$\frac{1}{1 - 3i}=\frac{1 + 3i}{(1 - 3i)(1 + 3i)}=\frac{1}{10}+\frac{3}{10}i$,所以复数$\frac{1}{1 - 3i}$的虚部是$\frac{3}{10}$。故选D。
易错警示
[深度解析]因为$\frac{1}{1 - 3i}=\frac{1 + 3i}{(1 - 3i)(1 + 3i)}=\frac{1}{10}+\frac{3}{10}i$,所以复数$\frac{1}{1 - 3i}$的虚部是$\frac{3}{10}$。故选D。
易错警示
3.在一组样本数据中,1,2,3,4出现的频率分别为p1,p2,p3,p4,且p1 + p2 + p3 + p4 = 1,则下面四种情形中,对应样本的标准差最大的一组是 ( )
A.p1 = p4 = 0.1,p2 = p3 = 0.4
B.p1 = p4 = 0.4,p2 = p3 = 0.1
C.p1 = p4 = 0.2,p2 = p3 = 0.3
D.p1 = p4 = 0.3,p2 = p3 = 0.2
A.p1 = p4 = 0.1,p2 = p3 = 0.4
B.p1 = p4 = 0.4,p2 = p3 = 0.1
C.p1 = p4 = 0.2,p2 = p3 = 0.3
D.p1 = p4 = 0.3,p2 = p3 = 0.2
答案:
3.B [命题点]样本标准差的求法
[深度解析]选项A中,E(X)=1×0.1 + 2×0.4 + 3×0.4 + 4×0.1 = 2.5,D(X)=(1 - 2.5)²×0.1 + (2 - 2.5)²×0.4 + (3 - 2.5)²×0.4 + (4 - 2.5)²×0.1 = 0.65。
选项B中,E(X)=1×0.4 + 2×0.1 + 3×0.1 + 4×0.4 = 2.5,D(X)=(1 - 2.5)²×0.4 + (2 - 2.5)²×0.1 + (3 - 2.5)²×0.1 + (4 - 2.5)²×0.4 = 1.85。
选项C中,E(X)=1×0.2 + 2×0.3 + 3×0.3 + 4×0.2 = 2.5,D(X)=(1 - 2.5)²×0.2 + (2 - 2.5)²×0.3 + (3 - 2.5)²×0.3 + (4 - 2.5)²×0.2 = 1.05。
选项D中,E(X)=1×0.3 + 2×0.2 + 3×0.2 + 4×0.3 = 2.5,D(X)=(1 - 2.5)²×0.3 + (2 - 2.5)²×0.2 + (3 - 2.5)²×0.2 + (4 - 2.5)²×0.3 = 1.45。
因此方差最大的一组是B,即标准差最大的一组是B。故选B。
一题多解:选项A中,E(X)=2.5,E(X²)=1×0.1 + 4×0.4 + 9×0.4 + 16×0.1 = 6.9,则D(X)=E(X²)-(E(X))²=6.9 - 2.5²。选项B中,E(X)=2.5,E(X²)=1×0.4 + 4×0.1 + 9×0.1 + 16×0.4 = 8.1,则D(X)=8.1 - 2.5²。选项C中,E(X)=2.5,E(X²)=1×0.2 + 4×0.3 + 9×0.3 + 16×0.2 = 7.3,则D(X)=7.3 - 2.5²。选项D中,E(X)=2.5,E(X²)=1×0.3 + 4×0.2 + 9×0.2 + 16×0.3 = 7.7,则D(X)=7.7 - 2.5²。由于6.9<7.3<7.7<8.1,因此标准差最大的一组为B。
关键点拨:也就是比较方差的大小,不必根据公式计算出标准差的值。本题的一题多解中利用了方差公式D(X)=E(X²)-(E(X))²。
[深度解析]选项A中,E(X)=1×0.1 + 2×0.4 + 3×0.4 + 4×0.1 = 2.5,D(X)=(1 - 2.5)²×0.1 + (2 - 2.5)²×0.4 + (3 - 2.5)²×0.4 + (4 - 2.5)²×0.1 = 0.65。
选项B中,E(X)=1×0.4 + 2×0.1 + 3×0.1 + 4×0.4 = 2.5,D(X)=(1 - 2.5)²×0.4 + (2 - 2.5)²×0.1 + (3 - 2.5)²×0.1 + (4 - 2.5)²×0.4 = 1.85。
选项C中,E(X)=1×0.2 + 2×0.3 + 3×0.3 + 4×0.2 = 2.5,D(X)=(1 - 2.5)²×0.2 + (2 - 2.5)²×0.3 + (3 - 2.5)²×0.3 + (4 - 2.5)²×0.2 = 1.05。
选项D中,E(X)=1×0.3 + 2×0.2 + 3×0.2 + 4×0.3 = 2.5,D(X)=(1 - 2.5)²×0.3 + (2 - 2.5)²×0.2 + (3 - 2.5)²×0.2 + (4 - 2.5)²×0.3 = 1.45。
因此方差最大的一组是B,即标准差最大的一组是B。故选B。
一题多解:选项A中,E(X)=2.5,E(X²)=1×0.1 + 4×0.4 + 9×0.4 + 16×0.1 = 6.9,则D(X)=E(X²)-(E(X))²=6.9 - 2.5²。选项B中,E(X)=2.5,E(X²)=1×0.4 + 4×0.1 + 9×0.1 + 16×0.4 = 8.1,则D(X)=8.1 - 2.5²。选项C中,E(X)=2.5,E(X²)=1×0.2 + 4×0.3 + 9×0.3 + 16×0.2 = 7.3,则D(X)=7.3 - 2.5²。选项D中,E(X)=2.5,E(X²)=1×0.3 + 4×0.2 + 9×0.2 + 16×0.3 = 7.7,则D(X)=7.7 - 2.5²。由于6.9<7.3<7.7<8.1,因此标准差最大的一组为B。
关键点拨:也就是比较方差的大小,不必根据公式计算出标准差的值。本题的一题多解中利用了方差公式D(X)=E(X²)-(E(X))²。
4.Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:I(t)=$\frac{K}{1 + e^{−0.23(t−53)}}$,其中K为最大确诊病例数.
当I(t)=0.95K时,标志着已初步遏制疫情,则t约为(ln19≈3) ( )
A.60
B.63
C.66
D.69
当I(t)=0.95K时,标志着已初步遏制疫情,则t约为(ln19≈3) ( )
A.60
B.63
C.66
D.69
答案:
4.C [命题点]指数式与对数式的互化
[深度解析]由$0.95K=\frac{K}{1 + e^{-0.23(t - 53)}}$得$e^{-0.23(t - 53)}=\frac{1}{19}$,两边取自然对数得$-0.23(t - 53)=-\ln19$,结合$\ln19\approx3$得$t\approx66$。故选C。
[深度解析]由$0.95K=\frac{K}{1 + e^{-0.23(t - 53)}}$得$e^{-0.23(t - 53)}=\frac{1}{19}$,两边取自然对数得$-0.23(t - 53)=-\ln19$,结合$\ln19\approx3$得$t\approx66$。故选C。
5.设O为坐标原点,直线x = 2与抛物线C:y² = 2px(p>0)交于D,E两点,若OD⊥OE,则C的焦点坐标为
( )
A.$(\frac{1}{4},0)$ B.$(\frac{1}{2},0)$
C.(1,0) D.(2,0)
( )
A.$(\frac{1}{4},0)$ B.$(\frac{1}{2},0)$
C.(1,0) D.(2,0)
答案:
5.B [命题点]直线与抛物线的位置关系,抛物线的几何性质
[深度解析]将x = 2代入抛物线方程y² = 2px中,得$y = \pm2\sqrt{p}$。不妨令$D(2, 2\sqrt{p})$,则$E(2, -2\sqrt{p})$。由$OD\perp OE$知$\overrightarrow{OD}\cdot\overrightarrow{OE}=0$,即$4 - 4p = 0$,得$p = 1$。因此抛物线$y² = 2x$的焦点坐标是$(\frac{1}{2}, 0)$。故选B。
快解:因为$\triangle DOE$是等腰直角三角形,因此$\angle xOD = 45^{\circ}$。将坐标$(2, 2)$代入抛物线方程$y² = 2px$中得$p = 1$,因此抛物线$y² = 2x$的焦点坐标为$(\frac{1}{2}, 0)$。
易错警示:抛物线$y² = 2px(p\gt0)$的焦点坐标是$(\frac{p}{2}, 0)$。因此$y² = 2x$的焦点坐标是$(\frac{1}{2}, 0)$,而非$(1, 0)$。
[深度解析]将x = 2代入抛物线方程y² = 2px中,得$y = \pm2\sqrt{p}$。不妨令$D(2, 2\sqrt{p})$,则$E(2, -2\sqrt{p})$。由$OD\perp OE$知$\overrightarrow{OD}\cdot\overrightarrow{OE}=0$,即$4 - 4p = 0$,得$p = 1$。因此抛物线$y² = 2x$的焦点坐标是$(\frac{1}{2}, 0)$。故选B。
快解:因为$\triangle DOE$是等腰直角三角形,因此$\angle xOD = 45^{\circ}$。将坐标$(2, 2)$代入抛物线方程$y² = 2px$中得$p = 1$,因此抛物线$y² = 2x$的焦点坐标为$(\frac{1}{2}, 0)$。
易错警示:抛物线$y² = 2px(p\gt0)$的焦点坐标是$(\frac{p}{2}, 0)$。因此$y² = 2x$的焦点坐标是$(\frac{1}{2}, 0)$,而非$(1, 0)$。
6. 已知向量$\vec{a}$,$\vec{b}$满足$|\vec{a}| = 5$,$|\vec{b}| = 6$,$\vec{a} \cdot \vec{b} = -6$,则$\cos\lt\vec{a},\vec{a} + \vec{b}\gt =$ ( )
A. $-\frac{31}{35}$ B. $-\frac{19}{35}$ C. $\frac{17}{35}$ D. $\frac{19}{35}$
答案:
6.D [命题点]平面向量的数量积及夹角
[深度解析]
∵|a| = 5,|b| = 6,a·b = -6,
∴a·(a + b) = |a|² + a·b = 25 - 6 = 19。又|a + b| = $\sqrt{a² + 2a·b + b²}$ = $\sqrt{25 - 12 + 36}$ = 7,
∴cos<a, a + b> = $\frac{a·(a + b)}{|a||a + b|}$ = $\frac{19}{5×7}$ = $\frac{19}{35}$。故选D。
关键点拨
cos<a, b> = $\frac{a·b}{|a||b|}$是根据向量数量积求向量夹角的常用方法。
[深度解析]
∵|a| = 5,|b| = 6,a·b = -6,
∴a·(a + b) = |a|² + a·b = 25 - 6 = 19。又|a + b| = $\sqrt{a² + 2a·b + b²}$ = $\sqrt{25 - 12 + 36}$ = 7,
∴cos<a, a + b> = $\frac{a·(a + b)}{|a||a + b|}$ = $\frac{19}{5×7}$ = $\frac{19}{35}$。故选D。
关键点拨
cos<a, b> = $\frac{a·b}{|a||b|}$是根据向量数量积求向量夹角的常用方法。
7. 在$\triangle ABC$中,$\cos C = \frac{2}{3}$,$AC = 4$,$BC = 3$,则$\cos B =$
( )
A. $\frac{1}{9}$ B. $\frac{1}{3}$ C. $\frac{1}{2}$ D. $\frac{2}{3}$
答案:
7.A [命题点]余弦定理在解三角形中的应用
[深度解析]
∵cosC = $\frac{2}{3}$,AC = 4,BC = 3,
∴AB² = AC² + BC² - 2AC·BCcosC = 16 + 9 - 2×4×3×$\frac{2}{3}$ = 9,
∴AB = 3。
∴cosB = $\frac{AB² + BC² - AC²}{2AB·BC}$ = $\frac{9 + 9 - 16}{2×3×3}$ = $\frac{1}{9}$。故选A。

一题多解
已知三角形的两边及其夹角的余弦值,常利用余弦定理求第三边;已知三角形的三边求夹角,常用余弦定理的推论求解。
7.A [命题点]余弦定理在解三角形中的应用
[深度解析]
∵cosC = $\frac{2}{3}$,AC = 4,BC = 3,
∴AB² = AC² + BC² - 2AC·BCcosC = 16 + 9 - 2×4×3×$\frac{2}{3}$ = 9,
∴AB = 3。
∴cosB = $\frac{AB² + BC² - AC²}{2AB·BC}$ = $\frac{9 + 9 - 16}{2×3×3}$ = $\frac{1}{9}$。故选A。

一题多解
已知三角形的两边及其夹角的余弦值,常利用余弦定理求第三边;已知三角形的三边求夹角,常用余弦定理的推论求解。
8. 如图为某几何体的三视图,则该几何体的表面积是( )

A. $6 + 4\sqrt{2}$
B. $4 + 4\sqrt{2}$
C. $6 + 2\sqrt{3}$
D. $4 + 2\sqrt{3}$
答案:
8.C [命题点]空间几何体的三视图及表面积
[深度解析]由几何体的三视图知,该几何体是一个侧棱与底面垂直,且底面是等腰直角三角形的三棱锥(提示:可将该三棱锥放在正方体中,更为直观),如图所示。这个三棱锥有三个面全等,即△PAB,△PAC,△ABC全等。
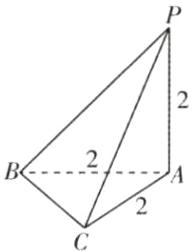
易知S△PAB + S△PAC + S△ABC = $\frac{1}{2}$×2×2×3 = 6。
又PB = PC = BC = 2$\sqrt{2}$,故S△PBC = $\frac{\sqrt{3}}{4}$×(2$\sqrt{2}$)² = 2$\sqrt{3}$。
因此该几何体的表面积是6 + 2$\sqrt{3}$。故选C。
关键点拨:观图特征求几何体表面积。由于正视图、侧视图和俯视图都是全等的等腰直角三角形,因此该几何体是一个三棱锥且一条侧棱与底面垂直。
8.C [命题点]空间几何体的三视图及表面积
[深度解析]由几何体的三视图知,该几何体是一个侧棱与底面垂直,且底面是等腰直角三角形的三棱锥(提示:可将该三棱锥放在正方体中,更为直观),如图所示。这个三棱锥有三个面全等,即△PAB,△PAC,△ABC全等。

易知S△PAB + S△PAC + S△ABC = $\frac{1}{2}$×2×2×3 = 6。
又PB = PC = BC = 2$\sqrt{2}$,故S△PBC = $\frac{\sqrt{3}}{4}$×(2$\sqrt{2}$)² = 2$\sqrt{3}$。
因此该几何体的表面积是6 + 2$\sqrt{3}$。故选C。
关键点拨:观图特征求几何体表面积。由于正视图、侧视图和俯视图都是全等的等腰直角三角形,因此该几何体是一个三棱锥且一条侧棱与底面垂直。
9. 已知$2\tan\theta - \tan(\theta + \frac{\pi}{4}) = 7$,则$\tan\theta =$ ( )
A. $-2$ B. $-1$ C. $1$ D. $2$
答案:
9.D [命题点]两角和的正切公式的应用
[深度解析]
∵2tanθ - tan(θ + $\frac{\pi}{4}$) = 7,
∴2tanθ - $\frac{1 + tanθ}{1 - tanθ}$ = 7,
∴2tanθ - 2tan²θ - 1 - tanθ = 7 - 7tanθ,即tan²θ - 4tanθ + 4 = 0,解得tanθ = 2。故选D。
[深度解析]
∵2tanθ - tan(θ + $\frac{\pi}{4}$) = 7,
∴2tanθ - $\frac{1 + tanθ}{1 - tanθ}$ = 7,
∴2tanθ - 2tan²θ - 1 - tanθ = 7 - 7tanθ,即tan²θ - 4tanθ + 4 = 0,解得tanθ = 2。故选D。
10. 若直线$l$与曲线$y = \sqrt{x}$和圆$x^{2}+y^{2}=\frac{1}{5}$都相切,则$l$的方程为( )
A. $y = 2x + 1$
B. $y = 2x+\frac{1}{2}$
C. $y=\frac{1}{2}x + 1$
D. $y=\frac{1}{2}x+\frac{1}{2}$
答案:
10.D [命题点]导数的几何意义,直线与圆相切的应用
[深度解析]设直线$l$与曲线$y = \sqrt{x}$相切于点$P(x_0,y_0)$,$x_0>0$,则由$(\sqrt{x})^\prime=\frac{1}{2\sqrt{x}}$知,曲线$y = \sqrt{x}$在点$P$处的切线方程为$y - \sqrt{x_0} = \frac{1}{2\sqrt{x_0}}(x - x_0)$,即$y = \frac{1}{2\sqrt{x_0}}x + \frac{\sqrt{x_0}}{2}$,也就是直线$l$的方程。由直线$l$与圆$x^2 + y^2 = \frac{1}{5}$相切得$\frac{\vert\frac{\sqrt{x_0}}{2}\vert}{\sqrt{1 + \frac{1}{4x_0}}} = \frac{\sqrt{5}}{5}$,解得$x_0 = 1$。故直线$l$的方程为$y = \frac{1}{2}x + \frac{1}{2}$。故选D。
快解(排除法):由直线与圆相切可知圆心到直线的距离为半径$\frac{\sqrt{5}}{5}$,因此符合条件的只有A、D。将A中直线方程代入$y = \sqrt{x}$,得$2x\sqrt{x} + 1 = 0$,无解;将D中直线方程代入$y = \sqrt{x}$,得$x - 2\sqrt{x} + 1 = 0$,解得$x = 1$,符合题意。
[深度解析]设直线$l$与曲线$y = \sqrt{x}$相切于点$P(x_0,y_0)$,$x_0>0$,则由$(\sqrt{x})^\prime=\frac{1}{2\sqrt{x}}$知,曲线$y = \sqrt{x}$在点$P$处的切线方程为$y - \sqrt{x_0} = \frac{1}{2\sqrt{x_0}}(x - x_0)$,即$y = \frac{1}{2\sqrt{x_0}}x + \frac{\sqrt{x_0}}{2}$,也就是直线$l$的方程。由直线$l$与圆$x^2 + y^2 = \frac{1}{5}$相切得$\frac{\vert\frac{\sqrt{x_0}}{2}\vert}{\sqrt{1 + \frac{1}{4x_0}}} = \frac{\sqrt{5}}{5}$,解得$x_0 = 1$。故直线$l$的方程为$y = \frac{1}{2}x + \frac{1}{2}$。故选D。
快解(排除法):由直线与圆相切可知圆心到直线的距离为半径$\frac{\sqrt{5}}{5}$,因此符合条件的只有A、D。将A中直线方程代入$y = \sqrt{x}$,得$2x\sqrt{x} + 1 = 0$,无解;将D中直线方程代入$y = \sqrt{x}$,得$x - 2\sqrt{x} + 1 = 0$,解得$x = 1$,符合题意。
11. 设双曲线$C:\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} = 1(a\gt0,b\gt0)$的左、右焦点分别为$F_1,F_2$,离心率为$\sqrt{5}$。$P$是$C$上一点,且$F_1P\perp F_2P$。若$\triangle PF_1F_2$的面积为$4$,则$a =$( )
A. $1$
B. $2$
C. $4$
D. $8$
答案:
11.A
[命题点]双曲线的定义及几何性质
[深度解析]不妨设点$P$在双曲线的右支上,则$\vert PF_1\vert - \vert PF_2\vert = 2a$ ①,又$PF_1\perp PF_2$,故$\vert PF_1\vert^2 + \vert PF_2\vert^2 = 4c^2$ ②。由①得$\vert PF_1\vert^2 + \vert PF_2\vert^2 - 2\vert PF_1\vert\vert PF_2\vert = 4a^2$ ③,由②③得$\vert PF_1\vert\vert PF_2\vert = 2c^2 - 2a^2$,所以$S_{\triangle PF_1F_2} = \frac{1}{2}\vert PF_1\vert\vert PF_2\vert = c^2 - a^2 = 4$。又$\frac{c}{a} = \sqrt{5}$,可得$a = 1$。故选A。
快解:由$PF_1\perp PF_2$及$S_{\triangle PF_1F_2} = 4$,知$S_{\triangle PF_1F_2} = \frac{b^2}{\tan45^{\circ}} = 4$,则$b = 2$。又$\frac{c}{a} = \sqrt{5}$,则$c^2 = 5a^2$,所以$a^2 + b^2 = 5a^2$,解得$a = 1$。
关键点拨:快解中利用了双曲线$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1(a>0,b>0)$的一个焦点三角形的面积公式,即点$P$在双曲线上(异于顶点),且$\angle F_1PF_2 = \alpha$,则$S_{\triangle PF_1F_2} = \frac{b^2}{\tan\frac{\alpha}{2}}$。
一题多解:由$\frac{c}{a} = \sqrt{5}$,得$c^2 = 5a^2$,即$a^2 + b^2 = 5a^2$,故$b = 2a$。不妨设点$P$在第一象限,坐标为$(x_0,y_0)$,由$P$在双曲线$C$上可得$\frac{x_0^2}{a^2} - \frac{y_0^2}{4a^2} = 1$ ①。由$F_1(-c,0)$,$F_2(c,0)$,可得$\overrightarrow{PF_1}\cdot\overrightarrow{PF_2} = 0$,即$x_0^2 + y_0^2 = c^2 = 5a^2$ ②。联立①②解得$y_0 = \frac{4\sqrt{5}a}{5}$,则$\triangle PF_1F_2$的面积为$\frac{1}{2}\cdot y_0\cdot 2c = 4a^2 = 4$,故$a = 1$。
[命题点]双曲线的定义及几何性质
[深度解析]不妨设点$P$在双曲线的右支上,则$\vert PF_1\vert - \vert PF_2\vert = 2a$ ①,又$PF_1\perp PF_2$,故$\vert PF_1\vert^2 + \vert PF_2\vert^2 = 4c^2$ ②。由①得$\vert PF_1\vert^2 + \vert PF_2\vert^2 - 2\vert PF_1\vert\vert PF_2\vert = 4a^2$ ③,由②③得$\vert PF_1\vert\vert PF_2\vert = 2c^2 - 2a^2$,所以$S_{\triangle PF_1F_2} = \frac{1}{2}\vert PF_1\vert\vert PF_2\vert = c^2 - a^2 = 4$。又$\frac{c}{a} = \sqrt{5}$,可得$a = 1$。故选A。
快解:由$PF_1\perp PF_2$及$S_{\triangle PF_1F_2} = 4$,知$S_{\triangle PF_1F_2} = \frac{b^2}{\tan45^{\circ}} = 4$,则$b = 2$。又$\frac{c}{a} = \sqrt{5}$,则$c^2 = 5a^2$,所以$a^2 + b^2 = 5a^2$,解得$a = 1$。
关键点拨:快解中利用了双曲线$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1(a>0,b>0)$的一个焦点三角形的面积公式,即点$P$在双曲线上(异于顶点),且$\angle F_1PF_2 = \alpha$,则$S_{\triangle PF_1F_2} = \frac{b^2}{\tan\frac{\alpha}{2}}$。
一题多解:由$\frac{c}{a} = \sqrt{5}$,得$c^2 = 5a^2$,即$a^2 + b^2 = 5a^2$,故$b = 2a$。不妨设点$P$在第一象限,坐标为$(x_0,y_0)$,由$P$在双曲线$C$上可得$\frac{x_0^2}{a^2} - \frac{y_0^2}{4a^2} = 1$ ①。由$F_1(-c,0)$,$F_2(c,0)$,可得$\overrightarrow{PF_1}\cdot\overrightarrow{PF_2} = 0$,即$x_0^2 + y_0^2 = c^2 = 5a^2$ ②。联立①②解得$y_0 = \frac{4\sqrt{5}a}{5}$,则$\triangle PF_1F_2$的面积为$\frac{1}{2}\cdot y_0\cdot 2c = 4a^2 = 4$,故$a = 1$。
12. 已知$5^{5}\lt8^{4}$,$13^{4}\lt8^{5}$。设$a = \log_{5}3$,$b = \log_{8}5$,$c = \log_{13}8$,则( )
A. $a\lt b\lt c$
B. $b\lt a\lt c$
C. $b\lt c\lt a$
D. $c\lt a\lt b$
答案:
12.A
[命题点]指数式与对数式的互化,换底公式,利用对数函数的单调性比较大小
[深度解析]$a - b = \log_53 - \log_85 = \frac{\lg3}{\lg5} - \frac{\lg5}{\lg8} = \frac{\lg3\cdot\lg8 - (\lg5)^2}{\lg5\cdot\lg8}$(提示:利用作差法比较)。由$\lg3\cdot\lg8 \lt (\frac{\lg3 + \lg8}{2})^2 = (\frac{\lg24}{2})^2 \lt (\frac{\lg25}{2})^2 = (\lg5)^2$(提示:借助基本不等式),可知$a - b \lt 0$,则$a \lt b$。因为$5^5 \lt 8^4$,所以$5\lg5 \lt 4\lg8$,所以$\frac{\lg5}{\lg8} \lt \frac{4}{5}$。因为$13^4 \lt 8^5$,所以$4\lg13 \lt 5\lg8$,所以$\frac{\lg8}{\lg13} \gt \frac{4}{5}$(提示:与中间量$\frac{4}{5}$比较),所以$\frac{\lg5}{\lg8} \lt \frac{\lg8}{\lg13}$,即$\log_85 \lt \log_{13}8$,所以$b \lt c$。综上可得$a \lt b \lt c$。故选A。
[命题点]指数式与对数式的互化,换底公式,利用对数函数的单调性比较大小
[深度解析]$a - b = \log_53 - \log_85 = \frac{\lg3}{\lg5} - \frac{\lg5}{\lg8} = \frac{\lg3\cdot\lg8 - (\lg5)^2}{\lg5\cdot\lg8}$(提示:利用作差法比较)。由$\lg3\cdot\lg8 \lt (\frac{\lg3 + \lg8}{2})^2 = (\frac{\lg24}{2})^2 \lt (\frac{\lg25}{2})^2 = (\lg5)^2$(提示:借助基本不等式),可知$a - b \lt 0$,则$a \lt b$。因为$5^5 \lt 8^4$,所以$5\lg5 \lt 4\lg8$,所以$\frac{\lg5}{\lg8} \lt \frac{4}{5}$。因为$13^4 \lt 8^5$,所以$4\lg13 \lt 5\lg8$,所以$\frac{\lg8}{\lg13} \gt \frac{4}{5}$(提示:与中间量$\frac{4}{5}$比较),所以$\frac{\lg5}{\lg8} \lt \frac{\lg8}{\lg13}$,即$\log_85 \lt \log_{13}8$,所以$b \lt c$。综上可得$a \lt b \lt c$。故选A。
13. 若$x,y$满足约束条件$\begin{cases}x + y\geq0\\2x - y\geq0\\x\leq1\end{cases}$,则$z = 3x + 2y$的最大值为______。
答案:
13.7 [命题点]线性规划
[深度解析]作出可行域,如图中阴影部分所示。由$z = 3x + 2y$可得$y = -\frac{3}{2}x + \frac{z}{2}$,平移直线$y = -\frac{3}{2}x$,可知直线$y = -\frac{3}{2}x + \frac{z}{2}$经过点$A(1,2)$时,$z$取得最大值$7$。

13.7 [命题点]线性规划
[深度解析]作出可行域,如图中阴影部分所示。由$z = 3x + 2y$可得$y = -\frac{3}{2}x + \frac{z}{2}$,平移直线$y = -\frac{3}{2}x$,可知直线$y = -\frac{3}{2}x + \frac{z}{2}$经过点$A(1,2)$时,$z$取得最大值$7$。

查看更多完整答案,请扫码查看


