《2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版》

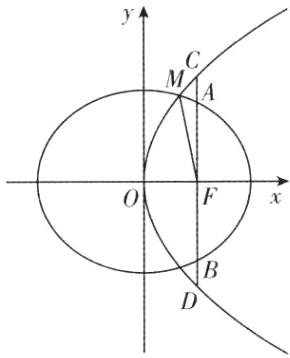
19.(本小题满分12分)已知椭圆$C_1:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a＞b＞0)$
　的右焦点$F$与抛物线$C_2$的焦点重合，$C_1$的中心与$C_2$ 的顶点重合。过$F$且与$x$轴垂直的直线交$C_1$于$A$，$B$ 两点，交$C_2$于$C$，$D$两点，且$\vert CD\vert=\frac{4}{3}\vert AB\vert$。
　(1)求$C_1$的离心率；
　(2)设$M$是$C_1$与$C_2$的公共点。若$\vert MF\vert = 5$，求$C_1$与$C_2$的标准方程。

答案：
19.[命题点]椭圆、抛物线的标准方程及其几何性质，抛物线的定义
[解]
(1)由已知可设C₂的方程为y² = 4cx，其中c = $\sqrt{a² - b²}$。
不妨设点A，C在第一象限，由题设得点A，B的纵坐标分别为$\frac{b²}{a}$，$-\frac{b²}{a}$；点C，D的纵坐标分别为2c， - 2c，故|AB| = $\frac{2b²}{a}$，|CD| = 4c。2分
由|CD| = $\frac{4}{3}$|AB|得4c = $\frac{8b²}{3a}$，即3×$\frac{c}{a}$ = 2 - 2($\frac{c}{a}$)²。
解得$\frac{c}{a}$ = - 2(舍去)，$\frac{c}{a}$ = $\frac{1}{2}$。
所以C₁的离心率为$\frac{1}{2}$。5分
(2)由
(1)知a = 2c，b = $\sqrt{3}$c。
故C₁：$\frac{x²}{4c²}$ + $\frac{y²}{3c²}$ = 1。6分
设M(x₀，y₀)，则$\frac{x₀²}{4c²}$ + $\frac{y₀²}{3c²}$ = 1，y₀² = 4cx₀。
故$\frac{x₀²}{4c²}$ + $\frac{4x₀}{3c}$ = 1。①8分

由于C₂的准线为x = - c，所以|MF| = x₀ + c，而|MF| = 5，故x₀ = 5 - c，代入①得$\frac{(5 - c)²}{4c²}$ + $\frac{4(5 - c)}{3c}$ = 1，即c² - 2c - 3 = 0，解得c = - 1(舍去)，c = 3。11分
所以C₁的标准方程为$\frac{x²}{36}$ + $\frac{y²}{27}$ = 1，C₂的标准方程为y² = 12x。12分

20.(本小题满分12分)如图,已知三棱柱ABC−A₁B₁C₁的底面是正三角形,侧面BB₁C₁C是矩形,M,N分别为BC,B₁C₁的中点,P为AM上一点.过B₁C₁和P 的平面交AB于E,交AC于F.
　　(1)证明:AA₁//MN,且平面A₁AMN⊥平面EB₁C₁F;
　　(2)设O为△A₁B₁C₁的中心.若AO//平面EB₁C₁F,且AO = AB,求直线B₁E与平面A₁AMN所成角的正弦值.
　　　　　　　　　　　　

答案：
20.[命题点]线线平行、面面垂直的判定，线面角的求解
(1)[证明]因为M,N分别为BC,B₁C₁的中点，所以MN//CC₁.
又由已知得AA₁//CC₁,故AA₁//MN. 2分
因为△ABC是正三角形，所以BC⊥AM. 3分
又B₁C₁⊥MN,AM∩MN = M,故B₁C₁⊥平面A₁AMN. 4分
所以平面A₁AMN⊥平面EB₁C₁F. 5分
(2)[解]由已知得AM⊥BC.以M为坐标原点，MA的方向为x轴正方向，|MB|为单位长，建立如图所示的空间直角坐标系M - xyz,则AB = 2,AM = $\sqrt{3}$

连接NP,则四边形AONP为平行四边形，故PM = $\frac{2\sqrt{3}}{3}$,E($\frac{2\sqrt{3}}{3}$,$\frac{1}{3}$,0). 6分
由
(1)知平面A₁AMN⊥平面ABC,作NQ⊥AM,垂足为Q,则NQ⊥平面ABC.
设Q(a,0,0),则NQ = ……,B₁(a, - 1,……)
故$\overrightarrow{B₁E}$ = ($\frac{2\sqrt{3}}{3}$ - a,$\frac{4}{3}$,……),|$\overrightarrow{B₁E}$| = $\frac{2\sqrt{10}}{3}$
又$\overrightarrow{n}$=(0, - 1,0)是平面A₁AMN的法向量，10分
故sin($\frac{\pi}{2}$ - ＜$\overrightarrow{n}$,$\overrightarrow{B₁E}$＞)=cos＜$\overrightarrow{n}$,$\overrightarrow{B₁E}$＞=$\frac{\overrightarrow{n}·\overrightarrow{B₁E}}{|\overrightarrow{n}|·|\overrightarrow{B₁E}|}$=$\frac{\sqrt{10}}{10}$
所以直线B₁E与平面A₁AMN所成角的正弦值为$\frac{\sqrt{10}}{10}$. 12分
一题多解
(2)连接NP.
因为AO//平面EB₁C₁F,平面AONP∩平面EB₁C₁F = NP,所以AO//NP. 6分
又三棱柱上下底面平行，平面A₁AMN∩平面ABC = AM,平面A₁AMN∩平面A₁B₁C₁ = A₁N,
所以ON//AP，故四边形ONPA是平行四边形. 8分
因为O为△ABC的中心，所以AN = 3ON,所以AM = 3AP.
又AO = $\frac{2}{3}$AB,所以PN = AO = $\frac{2}{3}$AB = $\frac{2}{3}$BC = $\frac{2}{3}$B₁C₁ = 3EF.
由
(1)知直线B₁E在平面A₁AMN内的射影为PN,
直线B₁E与平面A₁AMN所成角即为等腰梯形EFCB₁中B₁E与PN所成角. 10分
在等腰梯形EFCB₁中，令EF = 1,过E作EH⊥B₁C₁于H,则PN = B₁C₁ = 3,EH = $\sqrt{3}$,B₁H = 1,B₁E = $\sqrt{10}$,所以sin∠B₁EH = $\frac{B₁H}{B₁E}$ = $\frac{\sqrt{10}}{10}$,所以直线B₁E与平面A₁AMN所成角的正弦值为$\frac{\sqrt{10}}{10}$. 12分