《2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版》

1. 设集合$A = \{2, 3, 5, 7\}$，$B = \{1, 2, 3, 5, 8\}$，则$A\cap B =$ (　　　)
A. $\{1, 8\}$
B. $\{2, 5\}$
C. $\{2, 3, 5\}$
D. $\{1, 2, 3, 5, 7, 8\}$

答案： C [命题点]集合的交集运算
[深度解析]由题意得A∩B = {2,3,5}，故选C。

2. $(1 + 2i)(2 + i) =$ (　　　)
A. $-5i$
B. $5i$
C. $-5$
D. $5$

答案： B [命题点]复数的乘法运算
[深度解析](1 + 2i)(2 + i) = 2 + i + 4i + 2i² = 5i。故选B。

3. 若$D$为$\triangle ABC$的边$AB$的中点，则$\overrightarrow{CB} =$ (　　　)
A. $2\overrightarrow{CD} - \overrightarrow{CA}$
B. $2\overrightarrow{CA} - \overrightarrow{CD}$
C. $2\overrightarrow{CD} + \overrightarrow{CA}$
D. $2\overrightarrow{CA} + \overrightarrow{CD}$

答案： A [命题点]平面向量的线性运算
[深度解析]因为D是AB的中点，所以AD = DB。所以CB = CD + DB = CD + AD = CD + (CD - CA) = 2CD - CA；故选A。

4. 日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间.

把地球看成一个球(球心记为$O$)，地球上一点$A$的纬度是指$OA$与地球赤道所在平面所成角，点$A$处的水平面是指过点$A$且与$OA$垂直的平面. 在点$A$处放置一个日晷，若晷面与赤道所在平面平行，点$A$处的纬度为北纬$40^{\circ}$，则晷针与点$A$处的水平面所成角为 (　　　)
A. $20^{\circ}$
B. $40^{\circ}$
C. $50^{\circ}$
D. $90^{\circ}$

答案：
B [命题点]传统文化在立体几何中的应用
[深度解析]画出赤道和纬度的截面图，OA与地球赤道所在平面所成角为∠AOB。因为点A处的纬度为北纬40°，所以∠AOB = 40°。
过点A且与OA垂直的平面在截面图中为过点A的切线，则针与点A处的水平面所成的角，即针与点A处的切线所成的角α(提示:正确理解题意作出截面图，找到针与点A处的水平面所成角和点A处的纬度的关系)，可知α = 40°，故选B。

5. 某中学的学生积极参加体育锻炼，其中有$96\%$的学生喜欢足球或游泳，$60\%$的学生喜欢足球，$82\%$的学生喜欢游泳，则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是 (　　　)
A. $62\%$
B. $56\%$
C. $46\%$
D. $42\%$

答案：
C [命题点]统计数据的比例分布
[深度解析]该校60%的学生喜欢足球，82%的学生喜欢游泳，这两组数据包含既喜欢足球又喜欢游泳的学生，而96%的学生喜欢足球或游泳，则该校既喜欢足球又喜欢游泳的学生数占该校学生总数的比例为60% + 82% - 96% = 46%(提示:既喜欢足球又喜欢游泳的学生数 = 喜欢足球的学生数 + 喜欢游泳的学生数 - 喜欢足球或游泳的学生数)。故选C。
一题多解
设共有x%的学生只喜欢足球，有y%的学生只喜欢游泳，有z%的学生既喜欢足球又喜欢游泳，如图所示，列方程得
$\begin{cases}x + z = 60\\x + y + z = 96\\y + z = 82\end{cases}$
解得z = 46。故选C。

6. $3$名大学生利用假期到$2$个山村参加扶贫工作，每名大学生只去$1$个村，每个村至少去$1$人，则不同的分配方案共有 (　　　)
A. $4$种
B. $5$种
C. $6$种
D. $8$种

答案： C [命题点]排列组合在实际问题中的应用
[深度解析]根据题意，第一步，将3名大学生分成两组(一组1人，另一组2人)，有$C_{3}^1$种分法；第二步，将这两组大学生分配到2个山村，有$A_{2}^2$种分法。根据分步乘法计数原理，可得不同的分配方案有$C_{3}^1\cdot A_{2}^2$ = 6种。故选C。

7. 已知函数$f(x) = \lg(x^{2} - 4x - 5)$在$(a, +\infty)$单调递增，则$a$的取值范围是 (　　　)
A. $(-\infty, -1]$
B. $(-\infty, 2]$
C. $[2, +\infty)$
D. $[5, +\infty)$

答案： D [命题点]根据函数的单调性求参数的取值范围及复合函数的单调性
[深度解析]由x² - 4x - 5 ＞ 0，得x ＜ -1或x ＞ 5，所以函数f(x)的定义域为(-∞，-1)∪(5，+∞)(提示:复合函数问题重要前提是考虑定义域问题)。函数g(x) = lg(x² - 4x - 5)由函数y = lgμ，μ = x² - 4x - 5，x∈(-∞，-1)∪(5，+∞)复合而成。因为函数y = lgμ在(0，+∞)单调递增，μ = x² - 4x - 5在(-∞，-1)单调递减，在(5，+∞)单调递增，所以f(x)的单调递增区间是(5，+∞)。因为f(x)在(a，+∞)单调递增，所以a ≥ 5，即a的取值范围是[5，+∞)。故选D。

8. 若定义在$R$的奇函数$f(x)$在$(-\infty, 0)$单调递减，且$f(2) = 0$，则满足$xf(x - 1) \geq 0$的$x$的取值范围是 (　　　)
A. $[-1, 1]\cup[3, +\infty)$
B. $[-3, -1]\cup[0, 1]$
C. $[-1, 0]\cup[1, +\infty)$
D. $[-1, 0]\cup[1, 3]$

答案： D [命题点]函数的性质与不等式的求解
[深度解析]奇函数f(x)在(-∞，0)单调递减，且f
(2) = 0，则f(x)在(0，+∞)单调递减，且f(-2) = 0。由xf(x - 1) ≥ 0，得$\begin{cases}x \geq 0\\x - 1 \geq 0\\f(x - 1) \geq 0\end{cases}$或$\begin{cases}x \leq 0\\x - 1 \leq 0\\f(x - 1) \leq 0\end{cases}$，即$\begin{cases}x \geq 0\\x - 1 \leq 2\end{cases}$或$\begin{cases}x \leq 0\\x - 1 \geq -2\end{cases}$，解得$\{x|-1 \leq x \leq 0或1 \leq x \leq 3\}$。故选D。
关键点拨：求解不等式。

9. 我国新冠肺炎疫情防控进入常态化，各地有序推动复工复产. 下面是某地连续$11$天的复工、复产指数折线图.

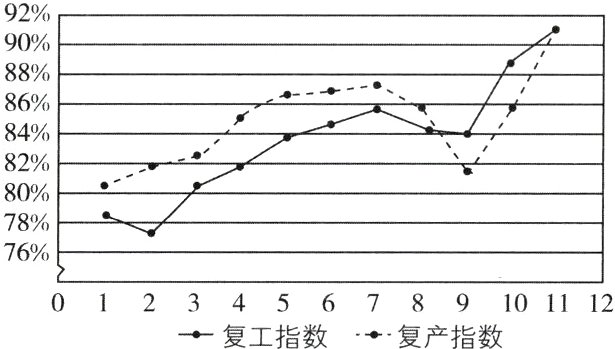
根据该折线图， (　　　)
A. 这$11$天复工指数和复产指数均逐日增加
B. 在这$11$天期间，复产指数的增量大于复工指数的增量
C. 第$3$天至第$11$天，复工指数和复产指数都超过$80\%$
D. 第$9$天至第$11$天，复产指数的增量大于复工指数的增量

答案： CD [命题点]统计图的应用
[深度解析]由题图可知第8,9天复工指数和复产指数均减小，故A错误；第1天时复工指数小于复产指数，第11天时两指数相等，故复产指数的增量小于复工指数的增量，故B错误；由题图可知第3天至第11天，复工复产指数都超过80%，故C正确；第9天至第11天，复产指数的增量大于复工指数的增量，故D正确。

10. 已知曲线$C:mx² + ny² = 1$，则（ ）
A. 若$m＞n＞0$，则$C$是椭圆，其焦点在$y$轴上
B. 若$m = n＞0$，则$C$是圆，其半径为$\sqrt{n}$
C. 若$mn＜0$，则$C$是双曲线，其渐近线方程为$y = ±\sqrt{\frac{m}{n}}$
D. 若$m = 0$，$n＞0$，则$C$是两条直线

答案： 10.ACD　[命题点]曲线方程表示的轨迹
[深度解析]由曲线C:mx²+ny²=1，当m＞n＞0时，$\frac{1}{n}$＞$\frac{1}{m}$＞0，曲线C:$\frac{x^{2}}{\frac{1}{m}}+\frac{y^{2}}{\frac{1}{n}} = 1$表示焦点在y轴上的椭圆，故A正确；当m=n＞0时，曲线C:x²+y²=$\frac{1}{n}$表示半径为$\sqrt{\frac{1}{n}}$的圆，故B错误；当mn＜0时，曲线C:mx²+ny²=1表示双曲线，令mx²+ny²=0，则其渐近线方程为y=±$\sqrt{-\frac{m}{n}}$x，故C正确；当m=0，n＞0时，曲线C:ny²=1，即y=±$\sqrt{\frac{1}{n}}$表示两条与x轴平行的直线，故D正确。故选ACD。
关键点拨|方程。