《2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版》

1. 设$z = \frac{2 + i}{1 + i^2 + i}$，则$z =$ (　　)
A. $1 - 2i$
B. $1 + 2i$
C. $2 - i$
D. $2 + i$

答案： B [命题点]共轭复数的概念及复数的四则运算
[深度解析]因为$z = \frac{2 + i}{1 + i^2 + i} = \frac{2 + i}{1 + (-1) + i} = \frac{2 + i}{i} = -(2 + i)i = 1 - 2i$，所以$\overline{z} = 1 + 2i$，故选B。

2. 设全集$U = R$，集合$M = \{x|x \lt 1\}$，$N = \{x|-1 \lt x \lt 2\}$，则$\{x|x \geq 2\} =$ (　　)
A. $\complement_U(M\cup N)$
B. $N\cup\complement_U M$
C. $\complement_U(M\cap N)$
D. $M\cup\complement_U N$

答案： A [命题点]集合的基本运算
[深度解析]因为$M = \{x|x ＜ 1\}$，$N = \{x|-1 ＜ x ＜ 2\}$，所以$M\cup N = \{x|x ＜ 2\}$，$\complement_{U}M = \{x|x\geq1\}$，$M\cap N = \{x|-1 ＜ x ＜ 1\}$，$\complement_{U}N = \{x|x\leq -1或x\geq2\}$，所以$\complement_{U}(M\cup N) = \{x|x\geq2\}$，$N\cup\complement_{U}M = \{x|x ＞ -1\}$，$\complement_{U}(M\cap N) = \{x|x\leq -1或x\geq1\}$，$M\cup\complement_{U}N = \{x|x ＜ 1或x\geq2\}$，故选A。

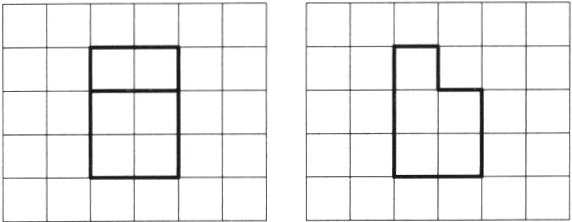
3. 如图，网格纸上绘制的是一个零件的三视图，网格小正方形的边长为1，则该零件的表面积为(　　)


A. 24
B. 26
C. 28
D. 30

答案：
D [命题点]空间几何体的三视图及表面积的计算
[深度解析]由三视图可知该零件是底面边长为2的正方形、高为3的长方体截去一个长、宽、高分别为2,1,1的小长方体的剩余部分，如图所示 ，则该零件的表面积$S = 2×2 + (2×3 - 1×1)×2 + 1×2 + 2×3 + 2×2 + 1×2 + 1×2 = 30$（另解：$S = 2×(2×2 + 2×3 + 2×3) - 2×1×1 = 30$），故选D。

4. 已知$f(x) = \frac{xe^x}{e^{ax} - 1}$是偶函数，则$a =$ (　　)
A. $-2$
B. $-1$
C. 1
D. 2

答案： D [命题点]函数的奇偶性
[深度解析]因为函数$f(x) = \frac{xe^{ax}}{e^{ax}-1}$是偶函数，且定义域为$\{x|x\neq0\}$，所以$f(-x) = f(x)$，即$\frac{xe^{ax}}{e^{ax}-1} = \frac{-xe^{-ax}}{e^{-ax}-1}$，即$\frac{xe^{ax}}{e^{ax}-1} = \frac{-xe^{ax}\cdot e^{-ax}}{1 - e^{ax}} = \frac{-xe^{ax - x}}{1 - e^{ax}} = \frac{xe^{ax - x}}{e^{ax}-1}$，所以$a - 1 = 1$，即$a = 2$，故选D。
一题多解：因为函数$f(x)$是偶函数，且定义域为$\{x|x\neq0\}$，所以$f(-1) = f(1)$，即$\frac{-e^{-a}}{e^{-a}-1} = \frac{e^{a}}{e^{a}-1}$，即$\frac{a - 1}{e^{a}-1} = \frac{e^{a}}{e^{a}-1}$，所以$a - 1 = 1$，即$a = 2$，故选D。

5. 设$O$为平面直角坐标系的坐标原点，在区域$\{(x,y)|1 \leq x^2 + y^2 \leq 4\}$内随机取一点，记该点为$A$，则直线$OA$的倾斜角不大于$\frac{\pi}{4}$的概率为(　　)
A. $\frac{1}{8}$
B. $\frac{1}{6}$
C. $\frac{1}{4}$
D. $\frac{1}{2}$

答案：
C [命题点]几何概型的概率计算
[深度解析]由题意可知区域$\{(x,y)|1\leq x^2 + y^2\leq4\}$表示如图所示的圆环，其面积$S = 4\pi - \pi = 3\pi$。其中满足直线$OA$的倾斜角不大于$\frac{\pi}{4}$的点$A$所在区域如图中阴影部分所示 ，其面积$S_0 = \frac{1}{4}×\pi×2^2 - \frac{1}{4}×\pi×1^2 = \frac{3\pi}{4}$。所以由几何概型的概率计算公式可得直线$OA$的倾斜角不大于$\frac{\pi}{4}$的概率$P = \frac{S_0}{S} = \frac{\frac{3\pi}{4}}{3\pi} = \frac{1}{4}$，故选C。

6. 已知函数$f(x)=\sin(\omega x + \varphi)$在区间$(\frac{\pi}{6},\frac{2\pi}{3})$单调递增，直线$x = \frac{\pi}{6}$和$x = \frac{2\pi}{3}$为函数$y = f(x)$的图像的两条对称轴，则$f(-\frac{5\pi}{12})=$（ ）
A. $-\frac{\sqrt{3}}{2}$
B. $-\frac{1}{2}$
C. $\frac{1}{2}$
D. $\frac{\sqrt{3}}{2}$

答案：
6.D　[命题点]正弦型函数的图像与性质
[深度解析]由题意画出f(x)图像的简图(如图).
因为函数f(x)=sin(ωx+φ)在区间$[\frac{\pi}{6},\frac{2\pi}{3})$单调递增，且直线x=$\frac{\pi}{6}$和直线x=$\frac{2\pi}{3}$为函数y=f(x)的图像的两条对称轴，所以$\frac{2\pi}{3}-\frac{\pi}{6}=\frac{T}{2}+\frac{T}{6}$，所以T=π，即$|\omega|=\frac{2\pi}{T}=2$，则ω=2或−2。而$f(\frac{\pi}{6})=-1$（提示：$\frac{\pi}{6}$为函数f(x)的极小值点），即sin(2×$\frac{\pi}{6}$+φ)=−1或sin(−2×$\frac{\pi}{6}$+φ)=−1，所以2×$\frac{\pi}{6}$+φ=$-\frac{\pi}{2}$+2kπ或−2×$\frac{\pi}{6}$+φ=$-\frac{\pi}{2}$+2kπ，k∈Z，即φ=$-\frac{5\pi}{6}$+2kπ或$\frac{\pi}{6}$+2kπ，k∈Z，所以f(x)=sin(2x−$\frac{5\pi}{6}$)或f(x)=sin(−2x+$\frac{\pi}{6}$)，所以f($-\frac{5\pi}{12}$)=sin(−$\frac{5\pi}{6}$−$\frac{5\pi}{6}$)=sin($-\frac{5\pi}{3}$)=sin$\frac{\pi}{3}$=$\frac{\sqrt{3}}{2}$或f($\frac{5\pi}{12}$)=sin($\frac{5\pi}{6}$−$\frac{\pi}{6}$)=$\frac{\sqrt{3}}{2}$，故选D。

7. 甲、乙两位同学从$6$种课外读物中各自选读$2$种，则这两人选读的课外读物中恰有$1$种相同的选法共有（ ）
A. $30$种
B. $60$种
C. $120$种
D. $240$种

答案： 7.C[命题点]排列组合、分步乘法计数原理
[深度解析]解法一:甲、乙两人选读的课外读物中恰有1种相同的选法共有$C_{6}^{1}C_{5}^{1}C_{4}^{1}=120$（种），故选C。
解法二:甲、乙从6种课外读物中各自选读2种，选法有$C_{6}^{2}×C_{6}^{2}=225$（种），其中，甲、乙选读的读物完全相同的选法有$C_{6}^{2}=15$（种），甲、乙选读的读物完全不同的选法有$C_{6}^{2}×C_{4}^{2}=90$（种），因此所求选法共有225−15−90=120（种），故选C。
解法三:从6种课外读物中任选3种，选法有$C_{6}^{3}=20$（种），然后把这3种读物分别安排为两人共同的读物、甲的读物、乙的读物，排列方法有3！种，因此所求选法共有$C_{6}^{3}×3！=120$（种），故选C。

8. 已知圆锥$PO$的底面半径为$\sqrt{3}$，$O$为底面圆心，$PA$，$PB$为圆锥的母线，$\angle AOB = 120^{\circ}$，若$\triangle PAB$的面积等于$\frac{9\sqrt{3}}{4}$，则该圆锥的体积为（ ）
A. $\pi$
B. $\sqrt{6}\pi$
C. $3\pi$
D. $3\sqrt{6}\pi$

答案：
8.B[命题点]圆锥的体积
[深度解析]因为∠AOB=120°，OA=OB=$\sqrt{3}$，所以AB=3。如图，设AB的中点为D，连接OD，则OD=$\frac{\sqrt{3}}{2}$。又因为△PAB为等腰三角形，面积为$\frac{9\sqrt{3}}{4}$，连接PD，则有$\frac{1}{2}×3×PD=\frac{9\sqrt{3}}{4}$，所以PD=$\frac{3\sqrt{3}}{2}$。在Rt△POD中，PO=$\sqrt{PD^{2}-OD^{2}}=\sqrt{6}$，所以该圆锥的体积为$\frac{1}{3}×\pi×(\sqrt{3})^{2}×\sqrt{6}=\sqrt{6}\pi$，故选B。

9. 已知$\triangle ABC$为等腰直角三角形，$AB$为斜边，$\triangle ABD$为等边三角形。若二面角$C - AB - D$为$150^{\circ}$，则直线$CD$与平面$ABC$所成角的正切值为（ ）
A. $\frac{1}{5}$
B. $\frac{\sqrt{2}}{5}$
C. $\frac{\sqrt{3}}{5}$
D. $\frac{2}{5}$

答案：
9.C　[命题点]二面角、直线与平面所成角
[深度解析]如图，设AB的中点为O，连接CO，DO，则CO⊥AB，DO⊥AB，于是∠COD即为二面角C−AB−D的平面角。过点D作DE⊥平面ABC，则点E一定落在CO的延长线上，∠DCE即直线CD与平面ABC所成的角。不妨设AB=2，在Rt△EOD中，DO=$\sqrt{3}$，∠EOD=180°−150°=30°，则DE=$\frac{\sqrt{3}}{2}$，EO=$\frac{3}{2}$。又CO=$\frac{1}{2}AB=1$，所以EC=$\frac{5}{2}$，tan∠DCE=$\frac{DE}{EC}=\frac{\sqrt{3}}{5}$。另解:在△DOC中，根据余弦定理得$CD^{2}=DO^{2}+CO^{2}-2DO·CO·cos150°=3 + 1 + 3 = 7$。所以sin∠DCE=$\frac{DE}{CD}=\frac{\sqrt{3}}{2\sqrt{7}}$，所以tan∠DCE=$\frac{\sqrt{3}}{5}$，故选C。

10. 已知等差数列$\{a_{n}\}$的公差为$3$，集合$S = \{ \cos a_{n}|n \in N^{*}\}$。若$S = \{a,b\}$，则$ab =$（ ）
A. $-1$
B. $-\frac{1}{2}$
C. $0$
D. $\frac{1}{2}$

答案： 10.B　[命题点]等差数列、三角函数的周期性、集合中元素的性质
[深度解析]因为等差数列$\{a_{n}\}$的公差为$\frac{2\pi}{3}$，即$a_{n + 3}=a_{n}+3k×\frac{2\pi}{3}=a_{n}+2k\pi$，$k\in N^{*}$，$cos a_{n + 3}=cos a_{n}$，这样集合$S=\{cos a_{n}|n\in N^{*}\}=\{cos a_{n}|n = 1,2,3\}=\{a,b\}$，因此$a_{1},a_{2},a_{3}$中有两个数的余弦值相等。满足$y = cos x = cos(x + \frac{2\pi}{3})$的y只有$y = \frac{1}{2}=cos(-\frac{\pi}{3})=cos\frac{\pi}{3}$或$y = -\frac{1}{2}=cos\frac{2\pi}{3}=cos\frac{4\pi}{3}$，两种情况对应第三个数的余弦值分别为$cos\pi = -1$或$cos2\pi = 1$，因此$ab = \frac{1}{2}×(-1)$或$ab = (-\frac{1}{2})×1$，均有$ab = -\frac{1}{2}$。故选B。
一题多解：由等差数列$\{a_{n}\}$的公差为$\frac{2\pi}{3}$，可知$cos a_{n}=cos\{a_{n}+3\}=cos a_{n + 3}$，所以数列$\{cos a_{n}\}$是周期为3的数列，所以$cos a_{1},cos a_{2},cos a_{3}$为一个周期的三项。由$S=\{a,b\}$可知S中只有两个元素，则$cos a_{1}=cos a_{2}$或$cos a_{1}=cos a_{3}$或$cos a_{2}=cos a_{3}$。
①若$cos a_{1}=cos(a_{1}+\frac{2\pi}{3})$，即$cos a_{1}=-\frac{1}{2}cos a_{1}-\frac{\sqrt{3}}{2}sin a_{1}$，可得$\begin{cases}cos a_{1}=\frac{1}{2}\\sin a_{1}=\frac{\sqrt{3}}{2}\end{cases}$或$\begin{cases}cos a_{1}=-\frac{1}{2}\\sin a_{1}=\frac{\sqrt{3}}{2}\end{cases}$，此时$cos(a_{1}+\frac{4\pi}{3})=-cos a_{1}+\frac{\sqrt{3}}{2}sin a_{1}=-1$或1，则$S=\{\frac{1}{2},-1\}$或$S=\{-\frac{1}{2},1\}$，则$ab = -\frac{1}{2}$。
②同理若$cos a_{1}=cos(a_{1}+\frac{4\pi}{3})$，可得$\begin{cases}cos a_{1}=\frac{1}{2}\\sin a_{1}=-\frac{\sqrt{3}}{2}\end{cases}$或$\begin{cases}cos a_{1}=-\frac{1}{2}\\sin a_{1}=-\frac{\sqrt{3}}{2}\end{cases}$，此时$cos(a_{1}+\frac{2\pi}{3})=-cos a_{1}-\frac{\sqrt{3}}{2}sin a_{1}=-1$或1，则$S=\{\frac{1}{2},1\}$或$\{-1,\frac{1}{2}\}$，则$ab = -\frac{1}{2}$。
③同理若$cos(a_{1}+\frac{2\pi}{3})=cos(a_{1}+\frac{4\pi}{3})$，可得$\begin{cases}cos a_{1}=0\\sin a_{1}=1\end{cases}$或$\begin{cases}cos a_{1}=0\\sin a_{1}=-1\end{cases}$，此时$cos(a_{1}+\frac{2\pi}{3})=cos(a_{1}+\frac{4\pi}{3})=-\frac{1}{2}$或$\frac{1}{2}$，则$S=\{\frac{1}{2},1\}$或$\{-1,\frac{1}{2}\}$，则$ab = -\frac{1}{2}$。
综上，可知$ab = -\frac{1}{2}$。故选B。