2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
17. (14分)已知直四棱柱ABCD−A₁B₁C₁D₁,AB//CD,AB⊥AD,AB = 2,AD = 3,DC = 4。
(1)证明:直线A₁B//平面DCC₁D₁;
(2)若直四棱柱ABCD−A₁B₁C₁D₁的体积为36,求二面角A₁−BD−A的大小。

答案:
17.[命题点]线面平行的判断、二面角的求解
(1)[证明]解法一(面面平行的性质定理):
∵AB//DC,AB⊄平面D₁C₁CD,DC⊂平面D₁C₁CD,
∴AB//平面D₁C₁CD. 2分
同理,由AA₁//DD₁,可知AA₁//平面D₁C₁CD. 3分
又AB∩AA₁=A,AB,AA₁⊂平面AB₁A₁B,
∴平面AB₁A₁B//平面D₁C₁CD. 4分
又
∵直线AB⊂平面AB₁A₁B,
∴直线AB//平面D₁C₁CD. 5分
解法二(线面平行的判定定理):如图,取CD的中点E,连接DE,BE.
∵AB//DE,且AB = $\frac{1}{2}$DC = DE,
∴四边形ABED是平行四边形,
∴AD//BE,且AD = BE. 2分
∵AD//A₁D₁,且AD = A₁D₁,
∴A₁D₁//BE,且A₁D₁ = BE.
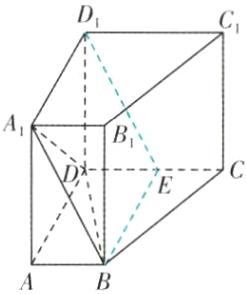
∴四边形A₁B₁ED₁是平行四边形,
∴A₁B₁//D₁E. 4分
∵A₁B₁⊄平面D₁C₁CD,D₁E⊂平面D₁C₁CD,
∴直线A₁B₁//平面D₁C₁CD. 5分
(2)[解]解法一:设AA₁ = h,则根据题意可得直四棱柱ABCD−A₁B₁C₁D₁的体积为$\frac{1}{2}$×(2 + 4)×3×h = 36,
解得h = 4. 7分
如图,在底面ABCD内过A作AF⊥BD,垂足点为F,连接A₁F.
∵AA₁⊥底面ABCD,AF,BD⊂平面ABCD,
∴AA₁⊥AF,AA₁⊥BD.
又
∵AA₁∩AF = A,AA₁,AF⊂平面AA₁F,
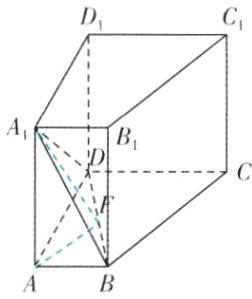
∴BD⊥平面AA₁F.
∵A₁F⊂平面AA₁F,
∴BD⊥A₁F,
∴∠A₁FA即为二面角A₁−BD−A的平面角. 10分
在Rt△ABD中,AB = 2,AD = 3,
∴BD = $\sqrt{4 + 9}$ = $\sqrt{13}$,
∴AF = $\frac{AB·AD}{BD}$ = $\frac{2×3}{\sqrt{13}}$ = $\frac{6}{\sqrt{13}}$. 12分
又
∵AA₁ = h = 4,
∴在Rt△AA₁F中,tan∠A₁FA = $\frac{AA₁}{AF}$ = $\frac{4}{\frac{6}{\sqrt{13}}}$ = $\frac{2\sqrt{13}}{3}$. 13分
∴二面角A₁−BD−A的大小为arctan$\frac{2\sqrt{13}}{3}$. 14分
解法二:设AA₁ = h,则根据题意可得直四棱柱ABCD−A₁B₁C₁D₁的体积为$\frac{1}{2}$×(2 + 4)×3×h = 36,
解得h = 4. 7分
以点D为原点,DA,DC,DD₁的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系D−xyz如图所示,
则D(0,0,0),B(3,2,0),A₁(3,0,4),则$\overrightarrow{DB}$ = (3,2,0),$\overrightarrow{DA₁}$ = (3,0,4). 9分
设平面A₁BD的法向量为$\overrightarrow{n₁}$ = (x,y,z),
则$\begin{cases}\overrightarrow{n₁}·\overrightarrow{DB}=0\\\overrightarrow{n₁}·\overrightarrow{DA₁}=0\end{cases}$,即$\begin{cases}3x + 2y = 0\\3x + 4z = 0\end{cases}$.

令x = 4,则平面A₁BD的一个法向量为$\overrightarrow{n₁}$ = (4,−6,−3). 11分
∵DD₁⊥平面ABD,
∴$\overrightarrow{n₂}$ = (0,0,1)是平面ABD的一个法向量. 12分
∵cos<$\overrightarrow{n₁}$,$\overrightarrow{n₂}$> = $\frac{\overrightarrow{n₁}·\overrightarrow{n₂}}{\vert\overrightarrow{n₁}\vert\vert\overrightarrow{n₂}\vert}$ = $\frac{−3}{\sqrt{61}}$, 13分
由图可知二面角A₁−BD−A是锐二面角,
∴二面角A₁−BD−A的余弦值为$\frac{3}{\sqrt{61}}$,则二面角A₁−BD−A的正切值为$\frac{2\sqrt{13}}{3}$,
∴二面角A₁−BD−A的大小为arctan$\frac{2\sqrt{13}}{3}$. 14分
17.[命题点]线面平行的判断、二面角的求解
(1)[证明]解法一(面面平行的性质定理):
∵AB//DC,AB⊄平面D₁C₁CD,DC⊂平面D₁C₁CD,
∴AB//平面D₁C₁CD. 2分
同理,由AA₁//DD₁,可知AA₁//平面D₁C₁CD. 3分
又AB∩AA₁=A,AB,AA₁⊂平面AB₁A₁B,
∴平面AB₁A₁B//平面D₁C₁CD. 4分
又
∵直线AB⊂平面AB₁A₁B,
∴直线AB//平面D₁C₁CD. 5分
解法二(线面平行的判定定理):如图,取CD的中点E,连接DE,BE.
∵AB//DE,且AB = $\frac{1}{2}$DC = DE,
∴四边形ABED是平行四边形,
∴AD//BE,且AD = BE. 2分
∵AD//A₁D₁,且AD = A₁D₁,
∴A₁D₁//BE,且A₁D₁ = BE.

∴四边形A₁B₁ED₁是平行四边形,
∴A₁B₁//D₁E. 4分
∵A₁B₁⊄平面D₁C₁CD,D₁E⊂平面D₁C₁CD,
∴直线A₁B₁//平面D₁C₁CD. 5分
(2)[解]解法一:设AA₁ = h,则根据题意可得直四棱柱ABCD−A₁B₁C₁D₁的体积为$\frac{1}{2}$×(2 + 4)×3×h = 36,
解得h = 4. 7分
如图,在底面ABCD内过A作AF⊥BD,垂足点为F,连接A₁F.
∵AA₁⊥底面ABCD,AF,BD⊂平面ABCD,
∴AA₁⊥AF,AA₁⊥BD.
又
∵AA₁∩AF = A,AA₁,AF⊂平面AA₁F,

∴BD⊥平面AA₁F.
∵A₁F⊂平面AA₁F,
∴BD⊥A₁F,
∴∠A₁FA即为二面角A₁−BD−A的平面角. 10分
在Rt△ABD中,AB = 2,AD = 3,
∴BD = $\sqrt{4 + 9}$ = $\sqrt{13}$,
∴AF = $\frac{AB·AD}{BD}$ = $\frac{2×3}{\sqrt{13}}$ = $\frac{6}{\sqrt{13}}$. 12分
又
∵AA₁ = h = 4,
∴在Rt△AA₁F中,tan∠A₁FA = $\frac{AA₁}{AF}$ = $\frac{4}{\frac{6}{\sqrt{13}}}$ = $\frac{2\sqrt{13}}{3}$. 13分
∴二面角A₁−BD−A的大小为arctan$\frac{2\sqrt{13}}{3}$. 14分
解法二:设AA₁ = h,则根据题意可得直四棱柱ABCD−A₁B₁C₁D₁的体积为$\frac{1}{2}$×(2 + 4)×3×h = 36,
解得h = 4. 7分
以点D为原点,DA,DC,DD₁的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系D−xyz如图所示,
则D(0,0,0),B(3,2,0),A₁(3,0,4),则$\overrightarrow{DB}$ = (3,2,0),$\overrightarrow{DA₁}$ = (3,0,4). 9分
设平面A₁BD的法向量为$\overrightarrow{n₁}$ = (x,y,z),
则$\begin{cases}\overrightarrow{n₁}·\overrightarrow{DB}=0\\\overrightarrow{n₁}·\overrightarrow{DA₁}=0\end{cases}$,即$\begin{cases}3x + 2y = 0\\3x + 4z = 0\end{cases}$.

令x = 4,则平面A₁BD的一个法向量为$\overrightarrow{n₁}$ = (4,−6,−3). 11分
∵DD₁⊥平面ABD,
∴$\overrightarrow{n₂}$ = (0,0,1)是平面ABD的一个法向量. 12分
∵cos<$\overrightarrow{n₁}$,$\overrightarrow{n₂}$> = $\frac{\overrightarrow{n₁}·\overrightarrow{n₂}}{\vert\overrightarrow{n₁}\vert\vert\overrightarrow{n₂}\vert}$ = $\frac{−3}{\sqrt{61}}$, 13分
由图可知二面角A₁−BD−A是锐二面角,
∴二面角A₁−BD−A的余弦值为$\frac{3}{\sqrt{61}}$,则二面角A₁−BD−A的正切值为$\frac{2\sqrt{13}}{3}$,
∴二面角A₁−BD−A的大小为arctan$\frac{2\sqrt{13}}{3}$. 14分
18.(14分)已知a,c∈R,函数f(x)=$\frac{x²+(3a+1)x+c}{x+a}$
(1)当a=0时,是否存在实数c,使得f(x)是奇函数?说明理由.
(2)若函数f(x)的图像过点(1,3),且函数f(x)的图像与x轴负半轴有两个交点,求c的值和a的取值范围.
答案:
18.[命题点]函数奇偶性的判断、函数与方程的应用
[解]
(1)若a = 0,则f(x) = $\frac{x^{2}+x + c}{x}$ = x + $\frac{c}{x}$ + 1,
要使函数有意义,则x ≠ 0,即f(x)的定义域为{x|x ≠ 0}.……2分
解法一:
∵y = x + $\frac{c}{x}$是奇函数,y = 1是偶函数,
∴函数f(x) = x + $\frac{c}{x}$ + 1为非奇非偶函数,不可能是奇函数,故不存在实数c,使得f(x)是奇函数. 5分
解法二:
∵f(−x) + f(x) = (−x - $\frac{c}{x}$ + 1) + (x + $\frac{c}{x}$ + 1) = 2 ≠ 0,
∴f(x)不可能是奇函数,故不存在实数c,使得f(x)是奇函数.
5分
(2)若函数f(x)的图像过点(1,3),则f
(1) = $\frac{1 + 3a + 1 + c}{1 + a}$ = $\frac{3a + 2 + c}{1 + a}$ = 3,
得3a + 2 + c = 3 + 3a,解得c = 1; 7分
此时f(x) = $\frac{x^{2}+(3a + 1)x + 1}{x + a}$,若函数f(x)的图像与x轴负半轴有两个交点,
则$\frac{x^{2}+(3a + 1)x + 1}{x + a}$ = 0,即x² + (3a + 1)x + 1 = 0(x ≠ -a)有两个不同的负实根. 8分
解法一(一元二次方程根的分布):设两根为x₁,x₂,
则$\begin{cases}\Delta=(3a + 1)^{2}-4>0\\x_{1}+x_{2}=-(3a + 1)<0\\x_{1}x_{2}=1>0\end{cases}$,得$\begin{cases}3a + 1>2或3a + 1<-2\\3a + 1>0\end{cases}$,
解得a > $\frac{1}{3}$ 11分
若x = -a是方程x² + (3a + 1)x + 1 = 0的根,
则a² - (3a + 1)a + 1 = 0,即2a² + a - 1 = 0,解得a = $\frac{1}{2}$或a = -1,
13分
∴a > $\frac{1}{3}$且a ≠ $\frac{1}{2}$,
即实数a的取值范围是($\frac{1}{3}$,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞). 14分
解法二(分离参数法):方程x² + (3a + 1)x + 1 = 0,即方程3a + 1 = $\frac{-x^{2}-1}{x}$ = -(x + $\frac{1}{x}$),
∴直线y = 3a + 1与函数h(x) = -(x + $\frac{1}{x}$)(x < 0)的图像有两个不同的交点. 9分
画出函数h(x) = -(x + $\frac{1}{x}$)(x < 0)的大致图像,如图.
由图可知,3a + 1 > 2,即a > $\frac{1}{3}$
11分
若x = -a是方程x² + (3a + 1)x + 1 = 0的根,则a² - (3a + 1)a + 1 = 0,即2a² + a - 1 = 0,解得a = $\frac{1}{2}$或a = -1,
13分
∴a > $\frac{1}{3}$且a ≠ $\frac{1}{2}$,即实数a的取值范围是($\frac{1}{3}$,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞). 14分

18.[命题点]函数奇偶性的判断、函数与方程的应用
[解]
(1)若a = 0,则f(x) = $\frac{x^{2}+x + c}{x}$ = x + $\frac{c}{x}$ + 1,
要使函数有意义,则x ≠ 0,即f(x)的定义域为{x|x ≠ 0}.……2分
解法一:
∵y = x + $\frac{c}{x}$是奇函数,y = 1是偶函数,
∴函数f(x) = x + $\frac{c}{x}$ + 1为非奇非偶函数,不可能是奇函数,故不存在实数c,使得f(x)是奇函数. 5分
解法二:
∵f(−x) + f(x) = (−x - $\frac{c}{x}$ + 1) + (x + $\frac{c}{x}$ + 1) = 2 ≠ 0,
∴f(x)不可能是奇函数,故不存在实数c,使得f(x)是奇函数.
5分
(2)若函数f(x)的图像过点(1,3),则f
(1) = $\frac{1 + 3a + 1 + c}{1 + a}$ = $\frac{3a + 2 + c}{1 + a}$ = 3,
得3a + 2 + c = 3 + 3a,解得c = 1; 7分
此时f(x) = $\frac{x^{2}+(3a + 1)x + 1}{x + a}$,若函数f(x)的图像与x轴负半轴有两个交点,
则$\frac{x^{2}+(3a + 1)x + 1}{x + a}$ = 0,即x² + (3a + 1)x + 1 = 0(x ≠ -a)有两个不同的负实根. 8分
解法一(一元二次方程根的分布):设两根为x₁,x₂,
则$\begin{cases}\Delta=(3a + 1)^{2}-4>0\\x_{1}+x_{2}=-(3a + 1)<0\\x_{1}x_{2}=1>0\end{cases}$,得$\begin{cases}3a + 1>2或3a + 1<-2\\3a + 1>0\end{cases}$,
解得a > $\frac{1}{3}$ 11分
若x = -a是方程x² + (3a + 1)x + 1 = 0的根,
则a² - (3a + 1)a + 1 = 0,即2a² + a - 1 = 0,解得a = $\frac{1}{2}$或a = -1,
13分
∴a > $\frac{1}{3}$且a ≠ $\frac{1}{2}$,
即实数a的取值范围是($\frac{1}{3}$,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞). 14分
解法二(分离参数法):方程x² + (3a + 1)x + 1 = 0,即方程3a + 1 = $\frac{-x^{2}-1}{x}$ = -(x + $\frac{1}{x}$),
∴直线y = 3a + 1与函数h(x) = -(x + $\frac{1}{x}$)(x < 0)的图像有两个不同的交点. 9分
画出函数h(x) = -(x + $\frac{1}{x}$)(x < 0)的大致图像,如图.
由图可知,3a + 1 > 2,即a > $\frac{1}{3}$
11分
若x = -a是方程x² + (3a + 1)x + 1 = 0的根,则a² - (3a + 1)a + 1 = 0,即2a² + a - 1 = 0,解得a = $\frac{1}{2}$或a = -1,
13分
∴a > $\frac{1}{3}$且a ≠ $\frac{1}{2}$,即实数a的取值范围是($\frac{1}{3}$,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞). 14分

查看更多完整答案,请扫码查看


