《2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版》

13. 若函数$f(x)=A\sin x - \sqrt{3}\cos x$的一个零点为$\frac{\pi}{3}$，则$A =$________，$f(\frac{\pi}{12}) =$________。

答案： 13. 1；$\sqrt{2}$
[命题点]两角差的正弦公式、三角函数的零点
[深度解析]依题意得$f(\frac{\pi}{3}) = A\times\frac{\sqrt{3}}{2} - \sqrt{3}\times\frac{1}{2} = 0$，解得$A = 1$。所以$f(x) = \sin x - \sqrt{3}\cos x = 2\sin(x - \frac{\pi}{3})$，所以$f(\frac{\pi}{12}) = 2\sin(\frac{\pi}{12} - \frac{\pi}{3}) = -\sqrt{2}$

14. 设函数$f(x)=\begin{cases}-(x - 1)^{2},&x\lt a\\x,&x\geq a\end{cases}$。若$f(x)$存在最小值，则$a$的一个取值为________；$a$的最大值为________。

答案： 14. 0（答案不唯一）；1
[命题点]根据分段函数的最值求参数
[深度解析]若$a = 0$，则函数$f(x) = \begin{cases}-x + 1, x ＜ 0 \\ (x - 2)^2, x \geq 0 \end{cases}$存在最小值0，所以a的一个取值可以为0。若$a ＜ 0$，则当$x ＜ a$时，$f(x) = -ax + 1$单调递增，函数$f(x)$不可能存在最小值。若$0 ＜ a \leq 2$，则当$x ＜ a$时，$f(x) = -ax + 1 \in (-a^2 + 1, +\infty)$；当$x \geq a$时，$f(x) = (x - 2)^2 \in [0, +\infty)$，若函数$f(x)$存在最小值，则$-a^2 + 1 \geq 0$，解得$0 ＜ a \leq 1$。若$a ＞ 2$，则当$x ＜ a$时，$f(x) = -ax + 1 \in (-a^2 + 1, +\infty)$；当$x \geq a$时，$f(x) = (x - 2)^2 \in [(a - 2)^2, +\infty)$，若函数$f(x)$存在最小值，则$-a^2 + 1 \geq (a - 2)^2$，不等式无解。
综上，$0 \leq a \leq 1$，所以a的最大值为1。

15. 已知数列$\{a_{n}\}$的各项均为正数，其前$n$项和$S_{n}$满足$a_{n}\cdot S_{n}=9(n = 1, 2, \cdots)$。给出下列四个结论：
①$\{a_{n}\}$的第2项小于3；②$\{a_{n}\}$为等比数列；③$\{a_{n}\}$为递减数列；④$\{a_{n}\}$中存在小于$\frac{1}{100}$的项。
其中所有正确结论的序号是________。

答案： 15. ①③④
思路导引
对于①，令$n = 1 \to a_1 = 3 \to$令$n = 2 \to a_2^2 + 3a_2 - 9 = 0 \to a_2 ＜ 3$；
对于②，$S_n = \frac{9}{a_n} \to S_{n - 1} = \frac{9}{a_{n - 1}}(n \geq 2) \to$两式作差得$a_n = \frac{9}{a_n} - \frac{9}{a_{n - 1}}$，若数列$\{a_n\}$为等比数列，则$\frac{a_{n + 1}}{a_n} = \frac{a_n}{a_{n - 1}}(n \geq 2) \to a_1 = 3 \neq a_2 \to$不成立；
对于③，$a_nS_n = a_{n + 1}S_{n + 1} \to \frac{a_n}{a_{n + 1}} = \frac{S_{n + 1}}{S_n} ＞ 1 \to a_n ＞ a_{n + 1} ＞ 0$；
对于④，采用“反证法”，先假设数列$\{a_n\}$的所有项均大于等于$\frac{1}{100}$，再推出与已知矛盾，从而否定假设
[命题点]数列的通项、数列的单调性
[深度解析]因为$a_nS_n = 9$，所以$a_1S_1 = 9$，又$a_1 ＞ 0$，所以$a_1 = 3$。$a_2S_2 = a_2(a_1 + a_2) = 9$，即$a_2^2 + 3a_2 - 9 = 0$，解得$a_2 = \frac{-3 + 3\sqrt{5}}{2} = 3\times\frac{\sqrt{5} - 1}{2} ＜ 3$，所以①正确。当$n \geq 2$时，由$S_n = \frac{9}{a_n}$，得$S_{n - 1} = \frac{9}{a_{n - 1}}$，两式作差可得$a_n = \frac{9}{a_n} - \frac{9}{a_{n - 1}}$（提示：利用公式$a_n = S_n - S_{n - 1}(n \geq 2)$求解），即$a_n = \frac{9(a_{n - 1} - a_n)}{a_na_{n - 1}}$，整理得$a_n^2 = \frac{9(a_{n - 1} - a_n)}{a_{n - 1}}$。若数列$\{a_n\}$为等比数列，则当$n \geq 2$时，$\frac{a_{n + 1}}{a_n} = \frac{9 - a_{n + 1}^2}{9} = \frac{a_n}{a_{n - 1}} = \frac{9 - a_n^2}{9}$，所以$a_{n + 1} = a_n$。又$a_1 = 3 \neq a_2$，所以数列$\{a_n\}$不为等比数列，所以②不正确。由题知$a_nS_n = a_{n + 1}S_{n + 1}$，所以$\frac{a_n}{a_{n + 1}} = \frac{S_{n + 1}}{S_n} ＞ 1$，所以$a_n ＞ a_{n + 1} ＞ 0$，所以数列$\{a_n\}$为递减数列，所以③正确。若数列$\{a_n\}$的所有项均大于等于$\frac{1}{100}$，即$a_n \geq \frac{1}{100}$，取$n ＞ 90000$，则$S_n ＞ 900$，于是$a_nS_n ＞ 9$，与已知矛盾，所以$\{a_n\}$中存在小于$\frac{1}{100}$的项，所以④正确。

16. (本小题满分13分)在△ABC中，sin2C = $\sqrt{3}$sinC。
(1)求∠C；
(2)若b = 6，且△ABC的面积为6$\sqrt{3}$，求△ABC的周长。

答案： [命题点]二倍角公式、余弦定理、三角形面积公式
[解]
(1)
∵sin2C = $\sqrt{3}$sinC，
∴2sinCcosC = $\sqrt{3}$sinC。 2分
又
∵C∈(0,π)，
∴sinC≠0，
∴cosC = $\frac{\sqrt{3}}{2}$。 4分
∴C = $\frac{\pi}{6}$。 5分
(2)
∵$S_{\triangle ABC}$ = $\frac{1}{2}$absinC = $6\sqrt{3}$，sinC = $\frac{1}{2}$，b = 6，
∴a = $4\sqrt{3}$。 8分
由余弦定理知$c^2$ = $a^2$ + $b^2$ - 2abcosC = 12，
∴c = $2\sqrt{3}$。
∴△ABC的周长为$6\sqrt{3}$ + 6。 13分

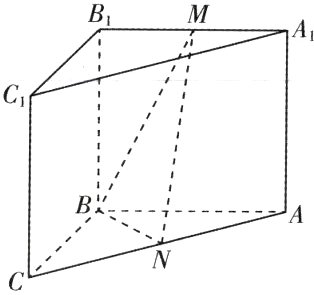
17. (本小题满分14分)如图，在三棱柱ABC - A₁B₁C₁中，侧面BCC₁B₁为正方形，平面BCC₁B₁⊥平面ABB₁A₁，AB = BC = 2，M，N分别为AB₁，AC的中点。
(1)求证：MN//平面BCC₁B₁；
(2)再从条件①、条件②这两个条件中选择一个作为已知，求直线AB与平面BMN所成角的正弦值。
条件①：AB⊥MN；
条件②：BM = MN。
注：如果选择条件①和条件②分别解答，按第一个解答计分。

答案：
[命题点]线面平行的判定、面面垂直的性质及利用空间向量求线面角的正弦值
(1)[证明]取BC中点D，连接BD，DN。在三棱柱ABC - $A_1B_1C_1$中，$A_1B_1$ // AB，$A_1B_1$ = AB。
因为M，N，D分别为$A_1B_1$，$A_1C_1$，BC的中点，

所以$B_1M$ // AB，$B_1M$ = $\frac{1}{2}$AB，DN // AB，DN = $\frac{1}{2}$AB，所以$B_1M$ // DN且$B_1M$ = DN，
所以四边形$B_1MND$为平行四边形，因此$B_1D$ // MN。 ......4分
又MN $\not\subset$平面$BCC_1B_1$，$B_1D$ $\subset$平面$BCC_1B_1$，
所以MN // 平面$BCC_1B_1$。 6分
(另解:取$A_1B_1$的中点H，连接MH，HN，利用MH // $BB_1$，HN // BC，证明平面MHN // 平面$BCC_1B_1$，再证明MN // 平面$BCC_1B_1$)
(2)[解]选条件①:
因为侧面$BCC_1B_1$为正方形，所以BC⊥$BB_1$。
又因为平面$BCC_1B_1$⊥平面$ABB_1A_1$，且平面$BCC_1B_1$∩平面$ABB_1A_1$ = $BB_1$，BC $\subset$平面$BCC_1B_1$，
所以BC⊥平面$ABB_1A_1$。
又因为AB $\subset$平面$ABB_1A_1$，所以AB⊥BC。
因为$B_1D$ // MN，AB⊥MN，所以AB⊥$B_1D$。
又$B_1D$∩BC = D，所以AB⊥平面$BCC_1B_1$。
因为$BB_1$ $\subset$平面$BCC_1B_1$，所以AB⊥$BB_1$。
所以在三棱柱ABC - $A_1B_1C_1$中，BA，BC，$BB_1$两两垂直，
故分别以BC，BA，$BB_1$所在直线为x轴、y轴、z轴，建立如图所示的空间直角坐标系。 8分

因为AB = BC = $BB_1$ = 2，
所以B(0,0,0)，N(1,1,0)，M(0,1,2)，A(0,2,0)，
所以$\overrightarrow{BN}$ = (1,1,0)，$\overrightarrow{BM}$ = (0,1,2)，$\overrightarrow{AB}$ = (0, - 2,0)。 10分
设平面BMN的法向量为$\overrightarrow{n}$ = (x,y,z)，
由$\begin{cases}\overrightarrow{BN}\cdot\overrightarrow{n}=0\\\overrightarrow{BM}\cdot\overrightarrow{n}=0\end{cases}$，得$\begin{cases}x + y = 0\\y + 2z = 0\end{cases}$，令x = 2，得$\overrightarrow{n}$ = (2, - 2,1)。 12分
设直线AB与平面BMN所成角为θ，
则sinθ = |cos＜$\overrightarrow{n}$,$\overrightarrow{AB}$＞| = $\frac{|\overrightarrow{n}\cdot\overrightarrow{AB}|}{|\overrightarrow{n}|\times|\overrightarrow{AB}|}$ = $\frac{| - 4|}{3\times2}$ = $\frac{2}{3}$。
所以直线AB与平面BMN所成角的正弦值为$\frac{2}{3}$。 14分
选条件②:
因为侧面$BCC_1B_1$为正方形，所以BC⊥$BB_1$。
又因为平面$BCC_1B_1$⊥平面$ABB_1A_1$，且平面$BCC_1B_1$∩平面$ABB_1A_1$ = $BB_1$，BC $\subset$平面$BCC_1B_1$，
所以BC⊥平面$ABB_1A_1$。
又因为AB $\subset$平面$ABB_1A_1$，所以AB⊥BC。
取AB中点H，连接HM，HN。
因为M，N，H分别为$A_1B_1$，$A_1C_1$，AB的中点，

所以$B_1B$ // MH，BC // HN。
又BC⊥$B_1B$，所以HN⊥MH。
因为AB = BC = 2，所以HN = BH = 1。
在△$MHB_1$和△MHN中，$B_1M$ = MN，BH = HN，公共边为MH，所以△$MHB_1$≌△MHN，
因此∠$MHB_1$ = ∠MHN = 90°，即MH⊥AB，故$BB_1$⊥AB。
所以在三棱柱ABC - $A_1B_1C_1$中，BA，BC，$BB_1$两两垂直，
故分别以BC，BA，$BB_1$所在直线为x轴、y轴、z轴，建立如图所示的空间直角坐标系。 8分
后同选①