2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 若$z = 1 + i$,则$\vert z^2 - 2z\vert =$ ( )
A. 0
B. 1
C. $\sqrt{2}$
D. 2
A. 0
B. 1
C. $\sqrt{2}$
D. 2
答案:
D [命题点]复数的基本运算
[深度解析]因为z = 1 + i,所以z² = (1 + i)² = 2i。所以z² - 2z = 2i - (2 + 2i) = -2,所以|z² - 2z| = 2,故选D。
[深度解析]因为z = 1 + i,所以z² = (1 + i)² = 2i。所以z² - 2z = 2i - (2 + 2i) = -2,所以|z² - 2z| = 2,故选D。
2. 设集合$A = \{x|x^2 - 4 \leq 0\}$,$B = \{x|2x + a \leq 0\}$,且$A\cap B =$
$\{x|-2 \leq x \leq 1\}$,则$a =$ ( )
A. -4
B. -2
C. 2
D. 4
$\{x|-2 \leq x \leq 1\}$,则$a =$ ( )
A. -4
B. -2
C. 2
D. 4
答案:
B [命题点]根据集合的运算求参数的值
[深度解析]由x² - 4 ≤ 0,解得 -2 ≤ x ≤ 2,所以集合A = [-2, 2]。由2x + a ≤ 0,解得x ≤ -$\frac{a}{2}$,则集合B = (-∞, -$\frac{a}{2}$]。又集合A ∩ B = [-2, 1],则 -$\frac{a}{2}$ = 1,所以a = -2,故选B。
[深度解析]由x² - 4 ≤ 0,解得 -2 ≤ x ≤ 2,所以集合A = [-2, 2]。由2x + a ≤ 0,解得x ≤ -$\frac{a}{2}$,则集合B = (-∞, -$\frac{a}{2}$]。又集合A ∩ B = [-2, 1],则 -$\frac{a}{2}$ = 1,所以a = -2,故选B。
3. 埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥. 以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A. $\frac{\sqrt{5} - 1}{4}$ B. $\frac{\sqrt{5} - 1}{2}$

C. $\frac{\sqrt{5} + 1}{4}$ D. $\frac{\sqrt{5} + 1}{2}$
A. $\frac{\sqrt{5} - 1}{4}$ B. $\frac{\sqrt{5} - 1}{2}$

C. $\frac{\sqrt{5} + 1}{4}$ D. $\frac{\sqrt{5} + 1}{2}$
答案:
C [命题点]数学文化和正四棱锥的几何性质
[深度解析]设正四棱锥的底面边长为a,高为h,侧面三角形底边上的高为h',则以h为边长的正方形的面积为h²,该四棱锥一个侧面三角形的面积为$\frac{1}{2}$ah'。故h² = $\frac{1}{2}$ah',且h² = h'² - ($\frac{a}{2}$)²。故h'² - ($\frac{a}{2}$)² = $\frac{1}{2}$ah',化简整理得4($\frac{h'}{a}$)² - 2$\frac{h'}{a}$ - 1 = 0,解得$\frac{h'}{a}$ = $\frac{\sqrt{5}+1}{4}$或$\frac{1 - \sqrt{5}}{4}$(舍),所以该四棱锥侧面三角形底边上的高与底面正方形的边长的比值为$\frac{\sqrt{5}+1}{4}$,故选C。

关键点拨:通过侧面三角形的面积得到一个关系式,并根据正四棱锥的高,侧面三角形底边上的高及底面正方形的边长的一半围成的是直角三角形,从而利用勾股定理得到另一个关系式,由两个关系式可求得结果。
C [命题点]数学文化和正四棱锥的几何性质
[深度解析]设正四棱锥的底面边长为a,高为h,侧面三角形底边上的高为h',则以h为边长的正方形的面积为h²,该四棱锥一个侧面三角形的面积为$\frac{1}{2}$ah'。故h² = $\frac{1}{2}$ah',且h² = h'² - ($\frac{a}{2}$)²。故h'² - ($\frac{a}{2}$)² = $\frac{1}{2}$ah',化简整理得4($\frac{h'}{a}$)² - 2$\frac{h'}{a}$ - 1 = 0,解得$\frac{h'}{a}$ = $\frac{\sqrt{5}+1}{4}$或$\frac{1 - \sqrt{5}}{4}$(舍),所以该四棱锥侧面三角形底边上的高与底面正方形的边长的比值为$\frac{\sqrt{5}+1}{4}$,故选C。

关键点拨:通过侧面三角形的面积得到一个关系式,并根据正四棱锥的高,侧面三角形底边上的高及底面正方形的边长的一半围成的是直角三角形,从而利用勾股定理得到另一个关系式,由两个关系式可求得结果。
4. 已知$A$为抛物线$C:y^2 = 2px(p \gt 0)$上一点,点$A$到$C$的焦点的距离为$12$,到$y$轴的距离为$9$,则$p =$ ( )
A. 2
B. 3
C. 6
D. 9
A. 2
B. 3
C. 6
D. 9
答案:
C [命题点]抛物线的定义
[深度解析]设抛物线的焦点为F,则|AF| = 12。根据抛物线的定义,点A到抛物线准线的距离d = 9 + $\frac{p}{2}$ = 12,解得p = 6,故选C。
一题多解:由“点A(-9, $\sqrt{18p}$)到焦点($\frac{p}{2}$, 0)的距离为12”,得$\sqrt{(-9 - \frac{p}{2})^2 + (\sqrt{18p} - 0)^2}$ = 12,将y = $\sqrt{18p}$代入上式得p² + 36p - 252 = 0,解得p = 6或 -42(舍负),故选C。
[深度解析]设抛物线的焦点为F,则|AF| = 12。根据抛物线的定义,点A到抛物线准线的距离d = 9 + $\frac{p}{2}$ = 12,解得p = 6,故选C。
一题多解:由“点A(-9, $\sqrt{18p}$)到焦点($\frac{p}{2}$, 0)的距离为12”,得$\sqrt{(-9 - \frac{p}{2})^2 + (\sqrt{18p} - 0)^2}$ = 12,将y = $\sqrt{18p}$代入上式得p² + 36p - 252 = 0,解得p = 6或 -42(舍负),故选C。
5.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xᵢ,yᵢ)(i = 1,2, …,20)得到下面的散点图:

10 20 30 40温度/℃
由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A.y = a + bx B.y = a + bx²
C.y = a + beˣ D.y = a + blnx
答案:
5.D [命题点]实际问题拟合函数的选择问题
[深度解析]根据题中散点图可知,散点大致分布在某一条“对数型”函数曲线的周围,而A选项是“直线型”的拟合函数,B选项是“抛物线型”的拟合函数,C选项是“指数型”的拟合函数,只有D选项的拟合函数更符合。故选D。
[深度解析]根据题中散点图可知,散点大致分布在某一条“对数型”函数曲线的周围,而A选项是“直线型”的拟合函数,B选项是“抛物线型”的拟合函数,C选项是“指数型”的拟合函数,只有D选项的拟合函数更符合。故选D。
6.函数f(x)=x⁴−2x²的图像在点(1,f(1))处的切线方程为( )
A.y = −2x−1
B.y = −2x + 1
C.y = 2x−3
D.y = 2x + 1
答案:
6.B [命题点]导数的几何意义
[深度解析]f'(x)=4x³ - 6x²,f'
(1)= - 2。又f
(1)= - 1,则函数f(x)的图像在(1, - 1)处的切线方程为y - (- 1)=f'
(1)·(x - 1),即y = - 2x + 1,故选B。
方法速记:y - f(x₀)=f'(x₀)(x - x₀)。
[深度解析]f'(x)=4x³ - 6x²,f'
(1)= - 2。又f
(1)= - 1,则函数f(x)的图像在(1, - 1)处的切线方程为y - (- 1)=f'
(1)·(x - 1),即y = - 2x + 1,故选B。
方法速记:y - f(x₀)=f'(x₀)(x - x₀)。
7.设函数f(x)=cos(ωx + $\frac{π}{6}$)在[−π,π]的图像大致如图,则f(x)的最小正周期为( )
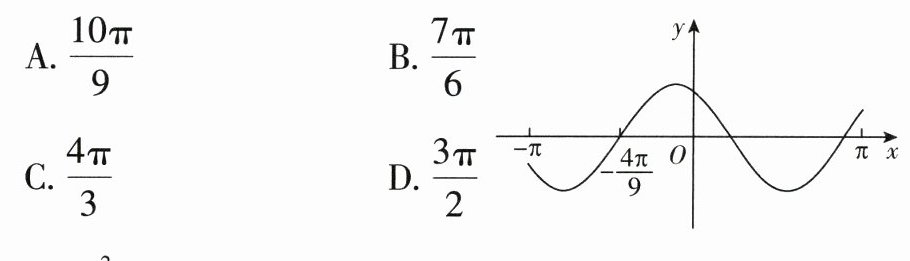
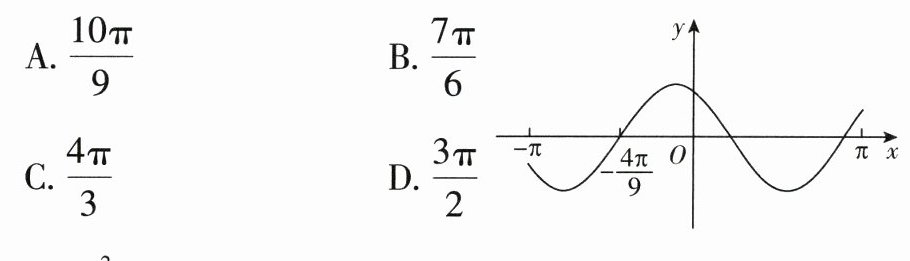
答案:
7.C [命题点]三角函数的图像与性质
[深度解析]由图像可得f(-$\frac{4π}{9}$)=cos(-$\frac{4π}{9}$ω + $\frac{π}{6}$)=0,所以 - $\frac{4π}{9}$ω + $\frac{π}{6}$=kπ + $\frac{π}{2}$,k∈Z,则ω = - $\frac{9}{4}$k - $\frac{3}{4}$,k∈Z。设函数f(x)的最小正周期为T,则T<2π<2T,即$\frac{2π}{|ω|}$<2π<$\frac{4π}{|ω|}$,所以1<|ω|<2。所以k = - 1,ω = $\frac{3}{2}$,经验证可知,当ω = $\frac{3}{2}$时与题图相符。所以f(x)的最小正周期T = $\frac{2π}{ω}$ = $\frac{4π}{3}$,故选C。
快解:由图像观察可得$\frac{3}{2}$T = 2π,所以T = $\frac{4π}{3}$。故选C。
[深度解析]由图像可得f(-$\frac{4π}{9}$)=cos(-$\frac{4π}{9}$ω + $\frac{π}{6}$)=0,所以 - $\frac{4π}{9}$ω + $\frac{π}{6}$=kπ + $\frac{π}{2}$,k∈Z,则ω = - $\frac{9}{4}$k - $\frac{3}{4}$,k∈Z。设函数f(x)的最小正周期为T,则T<2π<2T,即$\frac{2π}{|ω|}$<2π<$\frac{4π}{|ω|}$,所以1<|ω|<2。所以k = - 1,ω = $\frac{3}{2}$,经验证可知,当ω = $\frac{3}{2}$时与题图相符。所以f(x)的最小正周期T = $\frac{2π}{ω}$ = $\frac{4π}{3}$,故选C。
快解:由图像观察可得$\frac{3}{2}$T = 2π,所以T = $\frac{4π}{3}$。故选C。
8.(x + $\frac{y}{x}$)²(x + y)⁵的展开式中x³y²的系数为( )
A.5
B.10
C.15
D.20
答案:
8.C [命题点]二项式定理及其应用
[深度解析]因为(x + $\frac{y²}{x}$)(x + y)⁵ = x(x + y)⁵ + $\frac{y²}{x}$(x + y)⁵,(x + y)⁵的二项展开式的通项为$C_{5}^{r}$x⁵⁻ʳyʳ(r = 0,1,2,3,4,5),所以x(x + y)⁵的展开式中x³y²的系数为$C_{5}^{2}$ = 10,$\frac{y²}{x}$(x + y)⁵的展开式中x³y²的系数为$C_{5}^{4}$ = 5。所以(x + $\frac{y²}{x}$)(x + y)⁵的展开式中x³y²的系数为10 + 5 = 15。故选C。
[深度解析]因为(x + $\frac{y²}{x}$)(x + y)⁵ = x(x + y)⁵ + $\frac{y²}{x}$(x + y)⁵,(x + y)⁵的二项展开式的通项为$C_{5}^{r}$x⁵⁻ʳyʳ(r = 0,1,2,3,4,5),所以x(x + y)⁵的展开式中x³y²的系数为$C_{5}^{2}$ = 10,$\frac{y²}{x}$(x + y)⁵的展开式中x³y²的系数为$C_{5}^{4}$ = 5。所以(x + $\frac{y²}{x}$)(x + y)⁵的展开式中x³y²的系数为10 + 5 = 15。故选C。
9.已知α∈(0,π),且3cos2α−8cosα = 5,则sinα=( )
A.$\frac{\sqrt{5}}{3}$
B.$\frac{2}{3}$
C.$\frac{1}{3}$
D.$\frac{\sqrt{5}}{9}$
答案:
9.A [命题点]三角恒等变换以及同角三角函数基本关系
[深度解析]因为3cos2α - 8cosα = 5,所以3(2cos²α - 1) - 8cosα = 5,即3cos²α - 4cosα - 4 = 0,即(3cosα + 2)(cosα - 2) = 0,解得cosα = - $\frac{2}{3}$或cosα = 2(舍去)。又α∈(0,π),所以sinα = $\sqrt{1 - cos²α}$ = $\frac{\sqrt{5}}{3}$,故选A。
[深度解析]因为3cos2α - 8cosα = 5,所以3(2cos²α - 1) - 8cosα = 5,即3cos²α - 4cosα - 4 = 0,即(3cosα + 2)(cosα - 2) = 0,解得cosα = - $\frac{2}{3}$或cosα = 2(舍去)。又α∈(0,π),所以sinα = $\sqrt{1 - cos²α}$ = $\frac{\sqrt{5}}{3}$,故选A。
10.已知A,B,C为球O的球面上的三个点,⊙O₁为△ABC的外接圆.若⊙O₁的面积为4π,AB = BC = AC = OO₁,则球O的表面积为( )
A.64π
B.48π
C.36π
D.32π
答案:
10.A [命题点]球的表面积问题
[深度解析]设正三角形ABC的边长为a,⊙O₁的半径为r,球O的半径为R。由⊙O₁的面积为πr² = 4π,可得r = 2。又⊙O₁为△ABC的外接圆,则r = O₁A = $\frac{2}{3}$×$\frac{\sqrt{3}}{2}$a = 2,解得a = 2$\sqrt{3}$。在Rt△OO₁A中,R² = OA² = r² + OO₁² = 4 + 12 = 16,所以球O的表面积为4πR² = 64π,故选A。
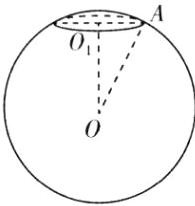
10.A [命题点]球的表面积问题
[深度解析]设正三角形ABC的边长为a,⊙O₁的半径为r,球O的半径为R。由⊙O₁的面积为πr² = 4π,可得r = 2。又⊙O₁为△ABC的外接圆,则r = O₁A = $\frac{2}{3}$×$\frac{\sqrt{3}}{2}$a = 2,解得a = 2$\sqrt{3}$。在Rt△OO₁A中,R² = OA² = r² + OO₁² = 4 + 12 = 16,所以球O的表面积为4πR² = 64π,故选A。

11.已知⊙M:x² + y²−2x−2y−2 = 0,直线l:2x + y + 2 = 0,P为l上的动点.过点P作⊙M的切线PA,PB,切点为A,B,当|PM|·|AB|最小时,直线AB的方程为( )
A.2x−y−1 = 0
B.2x + y−1 = 0
C.2x−y + 1 = 0
D.2x + y + 1 = 0
答案:
11.D [命题点]直线与圆的位置关系
[深度解析]由题意可知⊙M:(x - 1)² + (y - 1)² = 4,所以圆心M(1,1),半径为2。因为PA,PB是⊙M的切线,所以PA⊥AM,PB⊥BM。由圆的对称性可知PM⊥AB,所以S四边形PAMB = $\frac{1}{2}$|PM||AB| = 2S△PAM = |PA|·|AM|(提示:根据圆的切线长定理知|AM| = |BM|),所以|PM||AB|取得最小值时,|PA|·|AM|取得最小值。又|AM| = 2为定值,所以当|PA|最小时,|PM||AB|最小。因为|PA| = $\sqrt{|PM|² - |AM|²}$ = $\sqrt{|PM|² - 4}$,所以当|PM|取得最小值时,|PA|最小。又因为P为直线2x + y + 2 = 0上的动点,所以当PM⊥l时,|PM|取得最小值。此时直线PM的方程为y - 1 = $\frac{1}{2}$(x - 1),与直线l联立,可得P(- 1,0)。
解法一:由圆的切线结论知切点弦AB所在直线方程为(- 1 - 1)(x - 1) + (0 - 1)(y - 1) = 4,即2x + y + 1 = 0,故选D。
解法二:以线段PM为直径的圆的方程为(x - 1)(x + 1) + y(y - 1) = 0,整理得x² + y² - y - 1 = 0,与⊙M的方程x² + y² - 2x - 2y - 2 = 0作差可得直线AB的方程为2x + y + 1 = 0,故选D。

11.D [命题点]直线与圆的位置关系
[深度解析]由题意可知⊙M:(x - 1)² + (y - 1)² = 4,所以圆心M(1,1),半径为2。因为PA,PB是⊙M的切线,所以PA⊥AM,PB⊥BM。由圆的对称性可知PM⊥AB,所以S四边形PAMB = $\frac{1}{2}$|PM||AB| = 2S△PAM = |PA|·|AM|(提示:根据圆的切线长定理知|AM| = |BM|),所以|PM||AB|取得最小值时,|PA|·|AM|取得最小值。又|AM| = 2为定值,所以当|PA|最小时,|PM||AB|最小。因为|PA| = $\sqrt{|PM|² - |AM|²}$ = $\sqrt{|PM|² - 4}$,所以当|PM|取得最小值时,|PA|最小。又因为P为直线2x + y + 2 = 0上的动点,所以当PM⊥l时,|PM|取得最小值。此时直线PM的方程为y - 1 = $\frac{1}{2}$(x - 1),与直线l联立,可得P(- 1,0)。
解法一:由圆的切线结论知切点弦AB所在直线方程为(- 1 - 1)(x - 1) + (0 - 1)(y - 1) = 4,即2x + y + 1 = 0,故选D。
解法二:以线段PM为直径的圆的方程为(x - 1)(x + 1) + y(y - 1) = 0,整理得x² + y² - y - 1 = 0,与⊙M的方程x² + y² - 2x - 2y - 2 = 0作差可得直线AB的方程为2x + y + 1 = 0,故选D。

查看更多完整答案,请扫码查看


