《2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版》

1. 已知集合$U = \{−2,−1,0,1,2,3\}$，$A = \{−1,0,1\}$，$B = \{1,2\}$，则$\complement_U(A\cup B)=$( )
A. $\{−2,3\}$
B. $\{−2,2,3\}$
C. $\{−2,−1,0,3\}$
D. $\{−2,−1,0,2,3\}$

答案： A　[命题点]集合的基本运算
[深度解析]因为A∪B={−1,0,1,2}，所以∁U(A∪B)={−2,3}，故选A.

2. 若$\alpha$为第四象限角，则( )
A. $\cos2\alpha＞0$
B. $\cos2\alpha＜0$
C. $\sin2\alpha＞0$
D. $\sin2\alpha＜0$

答案： D　[命题点]象限角以及三角函数值的符号
[深度解析]因为α为第四象限角，所以−$\frac{\pi}{2}$+2kπ＜α＜2kπ，k∈Z，故−π+4kπ＜2α＜4kπ，k∈Z，所以2α为第三、四象限角或y轴负半轴上的角.所以cos2α的正负不确定，sin2α＜0，故选D.
一题多解：因为sin2α = 2sinαcosα＜0，故选D.

3. 在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天能完成$1200$份订单的配货，由于订单量大幅增加，导致订单积压。为解决困难，许多志愿者踊跃报名参加配货工作。已知该超市某日积压$500$份订单未配货，预计第二天的新订单超过$1600$份的概率为$0.05$。志愿者每人每天能完成$50$份订单的配货，为使第二天完成积压订单及当日订单的配货的概率不小于$0.95$，则至少需要志愿者( )
A. $10$名
B. $18$名
C. $24$名
D. $32$名

答案： B　[命题点]概率的理解和应用
[深度解析]由题意知预计第二天新订单除去超市配货1200份，若没有志愿者帮忙，则订单共会积压超过500+(1600−1200)=900份的概率为0.05，因此要使第二天完成积压订单及当日订单的配货的概率不小于0.95，所以至少需要志愿者$\frac{900}{50}$=18名，故选B.
关键点拨：则至少需要完成没有志愿者帮忙时会积压的订单总数

4. 北京天坛的圜丘坛为古代祭天的场所，分上、中、下三层。上层中心有一块圆形石板(称为天心石)，环绕天心石砌$9$块扇面形石板构成第一环，向外每环依次增加$9$块。下一层的第一环比上一层的最后一环多$9$块，向外每环依次也增加$9$块。已知每层环数相同，且下层比中层多$729$块，则三层共有扇面形石板(不含天心石)( )


A. $3699$块
B. $3474$块
C. $3402$块
D. $3339$块

答案： C　[命题点]等差数列的性质及其前n项和
[深度解析]设由内到外每环的扇面形石板的块数构成数列{an}，由题意知a1=9.又因为向外每环依次增加9块，下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块，所以数列{an}为公差为9的等差数列.
解法一:设每层环数为n(n∈N*)，则上层由内向外每环的扇面形石板的块数依次为a1,a2,...,an，中层由内向外每环的扇面形石板的块数依次为an+1,an+2,...,a2n，下层由内向外每环的扇面形石板的块数依次为a2n+1,a2n+2,...,a3n.由题意知(a2n+1+a2n+2+...+a3n)−(an+1+an+2+...+a2n)=729，由等差数列的性质知a2n+1−an+1=a2n+2−an+2=...=a3n−a2n=9n，所以9n²=729，得n=9.则数列{an}共有9×3=27项，故三层共有扇面形石板(不含天心石)的块数即为数列{an}的前27项和，即27×9+$\frac{27×26}{2}$×9=3402，故选C.
解法二:设每层环数为n(n∈N*)，设数列{an}的前n项和为Sn，由等差数列的性质知，Sn,S2n−Sn,S3n−S2n成等差数列，且(S3n−S2n)−(S2n−Sn)=9n²，则9n²=729，解得n=9.则数列{an}共有9×3=27项，故三层共有扇面形石板(不含天心石)的块数即为数列{an}的前27项和，即27×9+$\frac{27×26}{2}$×9=3402，故选C.

5.若过点(2,1)的圆与两坐标轴都相切,则圆心到直线2x−y−3=0的距离为　　　　　　　　　　　　(　　　)

A.$\frac{\sqrt{5}}{5}$　　　
　B.$\frac{2\sqrt{5}}{5}$　　
　C.$\frac{3\sqrt{5}}{5}$　　
　D.$\frac{4\sqrt{5}}{5}$

答案： 5.B　[命题点]圆的方程、性质以及点到直线的距离公式
[深度解析]因为过点(2,1)的圆与两坐标轴都相切，所以可设圆心坐标为(a,a)(a＞0)，且圆的半径r=a，所以圆的标准方程为(x - a)² + (y - a)² = a²。将点(2,1)的坐标代入圆的方程，得(2 - a)² + (1 - a)² = a²，展开可得a² - 6a + 5 = 0，因式分解为(a - 1)(a - 5) = 0，解得a = 1或a = 5，所以圆心坐标为(1,1)或(5,5)。故点(1,1)到直线2x - y - 3 = 0的距离为$\frac{|2×1 - 1 - 3|}{\sqrt{2² + 1²}}=\frac{2\sqrt{5}}{5}$，点(5,5)到直线2x - y - 3 = 0的距离为$\frac{|2×5 - 5 - 3|}{\sqrt{2² + 1²}}=\frac{2\sqrt{5}}{5}$，故选B。

6. 数列$\{a_n\}$中，$a_1 = 2$，$a_{m + n} = a_m a_n$。若$a_{k} + a_{k + 1} + a_{k + 2} + \cdots + a_{k + 10} = 2^{15} - 2^{5}$，则$k =$( )
A. 2
B. 3
C. 4
D. 5

答案： 6.C　[命题点]等比数列的判断、前n项和公式
[深度解析]因为数列{aₙ}中，aₘ₊ₙ = aₘaₙ，令m = 1，则aₙ₊₁ = a₁aₙ = 2aₙ，所以数列{aₙ}是首项为2，公比为2的等比数列，则aₖ₊ₙ = aₖ·2ⁿ = 2ᵏ⁺ⁿ。所以aₖ₊₁ + aₖ₊₂ +... + aₖ₊₁₀ = $\frac{a_{k + 1}(1 - 2^{10})}{1 - 2}$ = 2ᵏ⁺¹·(2¹⁰ - 1) = 2ᵏ⁺¹¹ - 2ᵏ⁺¹，则2ᵏ⁺¹¹ - 2ᵏ⁺¹ = 2¹⁵ - 2⁵，所以k = 4，故选C。

7. 如图是一个多面体的三视图，

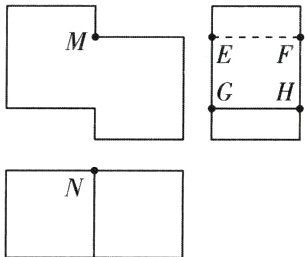
这个多面体某条棱的一个端点在正视图中对应的点为$M$，在俯视图中对应的点为$N$，则该端点在侧视图中对应的点为( )
A. $E$
B. $F$
C. $G$
D. $H$

答案：
7.A　[命题点]几何体的三视图
[深度解析]由多面体的三视图还原可得该几何体的直观图，如图所示.则所求端点在侧视图中对应的点为点E,故选A.

8. 设$O$为坐标原点，直线$x = a$与双曲线$C$：$\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1(a ＞ 0,b ＞ 0)$的两条渐近线分别交于$D$，$E$两点。若$\triangle ODE$的面积为$8$，则$C$的焦距的最小值为( )
A. 4
B. 8
C. 16
D. 32

答案：
8.B　[命题点]双曲线的几何性质以及最值的求解
[深度解析]双曲线C的渐近线方程为y = ±$\frac{b}{a}$x。
假设D(a,b)，则E(a, - b)，所以S△ODE = $\frac{1}{2}$·|DE|·a = ab = 8。又c² = a² + b² ≥ 2ab = 16，当且仅当a = b = 2√2时等号成立，所以c ≥ 4，焦距2c ≥ 8。则双曲线C的焦距的最小值为8，故选B。
关键点拨：
(1)根据双曲线性质写出渐近线方程并确定点D、E坐标；
(2)根据△ODE的面积求得ab = 8；
(3)结合c² = a² + b²求解。

9. 设函数$f(x) = \ln|2x + 1| - \ln|2x - 1|$，则$f(x)$( )
A. 是偶函数，且在$(\frac{1}{2}, +\infty)$单调递增
B. 是奇函数，且在$(-\frac{1}{2},\frac{1}{2})$单调递减
C. 是偶函数，且在$(-\infty, -\frac{1}{2})$单调递增
D. 是奇函数，且在$(-\infty, -\frac{1}{2})$单调递减

答案： 9.D　[命题点]函数的奇偶性和单调性
[深度解析]f(x)的定义域为{x|x ≠ ±$\frac{1}{2}$}，且f(-x) = ln|1 - 2x| - ln|1 + 2x| = ln|2x - 1| - ln|2x + 1| = - f(x)，所以f(x)为奇函数。当x ＞ 0时，f(x) = $\begin{cases}ln(2x + 1) - ln(1 - 2x),&0 ＜ x ＜ \frac{1}{2}\\ln(2x + 1) - ln(2x - 1),&x ＞ \frac{1}{2}\end{cases}$
当0 ＜ x ＜ $\frac{1}{2}$时，f(x) = ln$\frac{2x + 1}{1 - 2x}$ = ln(1 + $\frac{4x}{1 - 2x}$) = ln(1 - $\frac{2}{2x - 1}$)，易知f(x)单调递增；当x ＞ $\frac{1}{2}$时，f(x) = ln$\frac{2x + 1}{2x - 1}$ = ln(1 + $\frac{2}{2x - 1}$)，易知f(x)单调递减。因为f(x)为奇函数，且在(-$\frac{1}{2}$,$\frac{1}{2}$)上连续，所以f(x)在(-$\frac{1}{2}$,$\frac{1}{2}$)上单调递增，在(-∞,-$\frac{1}{2}$)和($\frac{1}{2}$,+∞)上单调递减，故选D。

10. 已知$\triangle ABC$是面积为$\frac{9\sqrt{3}}{4}$的等边三角形，且其顶点都在球$O$的球面上。若球$O$的表面积为$16\pi$，则$O$到平面$ABC$的距离为( )
A. $\sqrt{3}$
B. $\frac{3}{2}$
C. 1
D. $\frac{\sqrt{3}}{2}$

答案： 10.C
思路导引：球的表面积求半径R，勾股定理求O到平面ABC的距离d。
[命题点]球的表面积、球心到截面的距离
[深度解析]设等边三角形ABC的边长为a，因为其面积为$\frac{9\sqrt{3}}{4}$，所以$\frac{1}{2}$·a·$\frac{\sqrt{3}}{2}$a = $\frac{9\sqrt{3}}{4}$，解得a = 3。故△ABC的外接圆半径r = $\frac{2}{3}$·$\frac{\sqrt{3}}{2}$a = $\frac{\sqrt{3}}{3}$a = $\sqrt{3}$。设球O的半径为R，因为球O的表面积为16π，所以4πR² = 16π，得R² = 4。所以O到平面ABC的距离d = $\sqrt{R² - r²}$ = 1，故选C。

11. 若$2^{x} - 2^{-x} ＜ 3^{-x} - 3^{y}$，则( )
A. $\ln(y - x + 1) ＞ 0$
B. $\ln(y - x + 1) ＜ 0$
C. $\ln|x - y| ＞ 0$
D. $\ln|x - y| ＜ 0$

答案： 11.A
思路导引：已知2ˣ - 2ʸ ＜ 3⁻ˣ - 3⁻ʸ→设f(x) = 2ˣ - 3⁻ˣ→f(x) ＜ f(y)→f(x)的单调性→x ＜ y→y - x + 1 ＞ 1→ln(y - x + 1) ＞ 0。
[命题点]函数的单调性以及对数值正负的判断
[深度解析]由2ˣ - 2ʸ ＜ 3⁻ˣ - 3⁻ʸ可得2ˣ - 3⁻ˣ ＜ 2ʸ - 3⁻ʸ(提示:相同结构，构造函数)。设f(x) = 2ˣ - 3⁻ˣ，易知f(x)在R上为增函数。又f(x) ＜ f(y)，所以x ＜ y。则y - x + 1 ＞ 1，所以ln(y - x + 1) ＞ 0，故A正确，B错误。而当x = 1，y = 2时，ln|x - y| = 0，故C、D错误，故选A。
关键点拨：因为y = 2ˣ在R上为增函数，y = 3⁻ˣ在R上为减函数，所以易知f(x)在R上为增函数。

12. $0 - 1$周期序列在通信技术中有着重要应用。若序列$a_1a_2\cdots a_n\cdots$满足$a_i\in\{0,1\}(i = 1,2,\cdots)$，且存在正整数$m$，使得$a_{i + m} = a_i(i = 1,2,\cdots)$成立，则称其为$0 - 1$周期序列，并称满足$a_{i + m} = a_i(i = 1,2,\cdots)$的最小正整数$m$为这个序列的周期。对于周期为$m$的$0 - 1$序列$a_1a_2\cdots a_n\cdots$，$C(k)=\frac{1}{m}\sum_{i = 1}^{m}a_ia_{i + k}(k = 1,2,\cdots,m - 1)$是描述其性质的重要指标。下列周期为$5$的$0 - 1$序列中，满足$C(k)\leq\frac{1}{5}(k = 1,2,3,4)$的序列是( )
A. $11010\cdots$
B. $11011\cdots$
C. $10001\cdots$
D. $11001\cdots$

答案： 12.C　[命题点]新定义问题
[深度解析]因为0 - 1序列的周期为5，所以C(k) = $\frac{1}{5}$$\sum_{i = 1}^{5}$aᵢaᵢ₊ₖ(k = 1,2,3,4)，且aᵢ = aᵢ₊₅ = a₁，a₂ = a₂₊₅ = a₂。
对于A：C
(1) = $\frac{1}{5}$$\sum_{i = 1}^{5}$aᵢaᵢ₊₁ = $\frac{1}{5}$(a₁a₂ + a₂a₃ + a₃a₄ + a₄a₅ + a₅a₆) = $\frac{1}{5}$×(1 + 0 + 0 + 0 + 0) = $\frac{1}{5}$，C
(2) = $\frac{1}{5}$$\sum_{i = 1}^{5}$aᵢaᵢ₊₂ = $\frac{1}{5}$(a₁a₃ + a₂a₄ + a₃a₅ + a₄a₆ + a₅a₇) = $\frac{1}{5}$×(0 + 1 + 0 + 1 + 0) = $\frac{2}{5}$ ＞ $\frac{1}{5}$，不符合题意。
对于B：C
(1) = $\frac{1}{5}$$\sum_{i = 1}^{5}$aᵢaᵢ₊₁ = $\frac{1}{5}$×(1 + 0 + 0 + 1 + 1) = $\frac{3}{5}$ ＞ $\frac{1}{5}$，不符合题意。
对于C：C
(1) = $\frac{1}{5}$$\sum_{i = 1}^{5}$aᵢaᵢ₊₁ = $\frac{1}{5}$×(0 + 0 + 0 + 0 + 1) = $\frac{1}{5}$，
C
(2) = $\frac{1}{5}$$\sum_{i = 1}^{5}$aᵢaᵢ₊₂ = $\frac{1}{5}$×(0 + 0 + 0 + 0 + 0) = 0，
C
(3) = $\frac{1}{5}$$\sum_{i = 1}^{5}$aᵢaᵢ₊₃ = $\frac{1}{5}$×(0 + 0 + 0 + 0 + 0) = 0，
C
(4) = $\frac{1}{5}$$\sum_{i = 1}^{5}$aᵢaᵢ₊₄ = $\frac{1}{5}$×(1 + 0 + 0 + 0 + 0) = $\frac{1}{5}$，符合题意。
对于D：C
(1) = $\frac{1}{5}$$\sum_{i = 1}^{5}$aᵢaᵢ₊₁ = $\frac{1}{5}$×(1 + 0 + 0 + 0 + 1) = $\frac{2}{5}$ ＞ $\frac{1}{5}$，不符合题意。故选C。
关键点拨：解答本题的关键是理解题意并逐项判断C(k) = $\frac{1}{5}$$\sum_{i = 1}^{5}$aᵢaᵢ₊ₖ ≤ $\frac{1}{5}$(k = 1,2,3,4)是否成立。