2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
12.若2ᵃ + log₂a = 4ᵇ + 2log₄b,则( )
A.a>2b
B.a<2b
C.a>b²
D.a<b²
答案:
12.B
[命题点]函数单调性以及不等式放缩
[深度解析]由题设知2ᵃ + log₂a = 4ᵇ + 2log₄b = 2²ᵇ + log₂b。又log₂b = log₂(2b) - 1,所以2ᵃ + log₂a = 2²ᵇ + log₂(2b) - 1,从而2ᵃ + log₂a < 2²ᵇ + log₂(2b)。令函数f(x) = 2ˣ + log₂x,x∈(0,+∞),则有f(a) < f(2b),显然f(x)在(0,+∞)上为增函数,所以a < 2b,故选B。
[命题点]函数单调性以及不等式放缩
[深度解析]由题设知2ᵃ + log₂a = 4ᵇ + 2log₄b = 2²ᵇ + log₂b。又log₂b = log₂(2b) - 1,所以2ᵃ + log₂a = 2²ᵇ + log₂(2b) - 1,从而2ᵃ + log₂a < 2²ᵇ + log₂(2b)。令函数f(x) = 2ˣ + log₂x,x∈(0,+∞),则有f(a) < f(2b),显然f(x)在(0,+∞)上为增函数,所以a < 2b,故选B。
13.若x,y满足约束条件$\begin{cases}2x + y−2\leq0\\x−y−1\geq0\\y + 1\geq0\end{cases}$,则z = x + 7y的最大值为______.
答案:
13.1 [命题点]线性规划
[深度解析]如图,作出约束条件表示的可行域(如图中阴影部分所示)。目标函数z = x + 7y,可化为y = - $\frac{1}{7}$x + $\frac{z}{7}$,平移直线y = - $\frac{1}{7}$x可知,当直线经过点A(1,0)时,在y轴上的截距最大,此时z = 1 + 7×0 = 1。
快解:x + 7y的最值在顶点处取得。A(1,0),此时z = 1;B(0, - 1),此时z = - 7;C($\frac{3}{2}$, - 1),此时z = - $\frac{11}{2}$。故z的最大值为1。

13.1 [命题点]线性规划
[深度解析]如图,作出约束条件表示的可行域(如图中阴影部分所示)。目标函数z = x + 7y,可化为y = - $\frac{1}{7}$x + $\frac{z}{7}$,平移直线y = - $\frac{1}{7}$x可知,当直线经过点A(1,0)时,在y轴上的截距最大,此时z = 1 + 7×0 = 1。
快解:x + 7y的最值在顶点处取得。A(1,0),此时z = 1;B(0, - 1),此时z = - 7;C($\frac{3}{2}$, - 1),此时z = - $\frac{11}{2}$。故z的最大值为1。

14.设a,b为单位向量,且|a + b| = 1,则|a - b| =______.
答案:
14.√3 [命题点]平面向量模的运算
[深度解析]因为a,b为单位向量,且|a + b| = 1,所以|a + b|² = a² + b² + 2a·b = 1,所以2a·b = - 1。又因为|a - b|² = (a + b)² - 4a·b = 1 - 2×(- 1) = 3,所以|a - b| = $\sqrt{3}$。
[深度解析]因为a,b为单位向量,且|a + b| = 1,所以|a + b|² = a² + b² + 2a·b = 1,所以2a·b = - 1。又因为|a - b|² = (a + b)² - 4a·b = 1 - 2×(- 1) = 3,所以|a - b| = $\sqrt{3}$。
15.已知F为双曲线C:$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$(a>0,b>0)的右焦点,A为C的右顶点,B为C上的点,且BF垂直于x轴.若AB的斜率为3,则C的离心率为______.
答案:
15.2 [命题点]双曲线的几何性质
[深度解析]因为BF⊥x轴,所以|BF| = $\frac{b²}{a}$。而|AF| = c - a,根据直线AB的斜率为3可得$\frac{|BF|}{|AF|}$ = $\frac{\frac{b²}{a}}{c - a}$ = $\frac{b²}{a(c - a)}$ = $\frac{c² - a²}{a(c - a)}$ = $\frac{c + a}{a}$ = e + 1 = 3,解得e = 2,故C的离心率为2。
一题多解
设A(a,0),F(c,0),因为BF⊥x轴,所以可设B(c,y)。又点B(c,y)在双曲线上,所以$\frac{c²}{a²}$ - $\frac{y²}{b²}$ = 1,解得y = ±$\frac{b²}{a}$。又直线AB的斜率为3,则y>0,所以B(c,$\frac{b²}{a}$)。由斜率公式得$\frac{\frac{b²}{a}}{c - a}$ = 3,整理得b² = 3ac - 3a²。又b² = c² - a²,则c² - 3ac + 2a² = 0,即e² - 3e + 2 = 0,解得e = 2或e = 1(舍去),故C的离心率为2。
方法速记
椭圆、双曲线的通径长为$\frac{2b²}{a}$。
[深度解析]因为BF⊥x轴,所以|BF| = $\frac{b²}{a}$。而|AF| = c - a,根据直线AB的斜率为3可得$\frac{|BF|}{|AF|}$ = $\frac{\frac{b²}{a}}{c - a}$ = $\frac{b²}{a(c - a)}$ = $\frac{c² - a²}{a(c - a)}$ = $\frac{c + a}{a}$ = e + 1 = 3,解得e = 2,故C的离心率为2。
一题多解
设A(a,0),F(c,0),因为BF⊥x轴,所以可设B(c,y)。又点B(c,y)在双曲线上,所以$\frac{c²}{a²}$ - $\frac{y²}{b²}$ = 1,解得y = ±$\frac{b²}{a}$。又直线AB的斜率为3,则y>0,所以B(c,$\frac{b²}{a}$)。由斜率公式得$\frac{\frac{b²}{a}}{c - a}$ = 3,整理得b² = 3ac - 3a²。又b² = c² - a²,则c² - 3ac + 2a² = 0,即e² - 3e + 2 = 0,解得e = 2或e = 1(舍去),故C的离心率为2。
方法速记
椭圆、双曲线的通径长为$\frac{2b²}{a}$。
16. 如图,在三棱锥P−ABC的平面展开图
中,AC = 1,AB = AD = $\sqrt{3}$,AB⊥AC,AB⊥
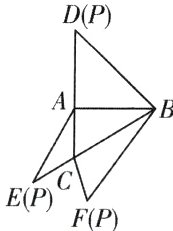
AD,∠CAE = 30°,则cos∠FCB =
________.
中,AC = 1,AB = AD = $\sqrt{3}$,AB⊥AC,AB⊥

AD,∠CAE = 30°,则cos∠FCB =
________.
答案:
-$\frac{1}{4}$
思路导引
[命题点]立体几何平面展开图及解三角形问题
[深度解析]在△ABC中,AB⊥AC,AC = 1,AB = $\sqrt{3}$,
所以BC = 2。
在△ABD中,AB⊥AD,AD = $\sqrt{3}$,AB = $\sqrt{3}$,所以BD = $\sqrt{6}$。
在△ACE中,AC = 1,AE = AD = $\sqrt{3}$,∠CAE = 30°,由余弦定理得
CE² = AC² + AE² - 2AC·AE·cos∠CAE = 1 + 3 - 2×1×$\sqrt{3}$×$\frac{\sqrt{3}}{2}$ = 1,所以CE = 1。
在△BCF中,BC = 2,FC = CE = 1,BF = BD = $\sqrt{6}$,由余弦定理得cos∠FCB = $\frac{FC² + BC² - FB²}{2FC·BC}$ = $\frac{1 + 4 - 6}{2×1×2}$ = -$\frac{1}{4}$。
思路导引
[命题点]立体几何平面展开图及解三角形问题
[深度解析]在△ABC中,AB⊥AC,AC = 1,AB = $\sqrt{3}$,
所以BC = 2。
在△ABD中,AB⊥AD,AD = $\sqrt{3}$,AB = $\sqrt{3}$,所以BD = $\sqrt{6}$。
在△ACE中,AC = 1,AE = AD = $\sqrt{3}$,∠CAE = 30°,由余弦定理得
CE² = AC² + AE² - 2AC·AE·cos∠CAE = 1 + 3 - 2×1×$\sqrt{3}$×$\frac{\sqrt{3}}{2}$ = 1,所以CE = 1。
在△BCF中,BC = 2,FC = CE = 1,BF = BD = $\sqrt{6}$,由余弦定理得cos∠FCB = $\frac{FC² + BC² - FB²}{2FC·BC}$ = $\frac{1 + 4 - 6}{2×1×2}$ = -$\frac{1}{4}$。
17. (本小题满分12分)设$\{a_n\}$是公比不为1的等比数列,$a_1$为$a_2$,$a_3$的等差中项.
(1)求$\{a_n\}$的公比;
(2)若$a_1$ = 1,求数列$\{na_n\}$的前n项和.
(1)求$\{a_n\}$的公比;
(2)若$a_1$ = 1,求数列$\{na_n\}$的前n项和.
答案:
[命题点]等比数列的基本运算与错位相减法求数列的前n项和
[解]
(1)设$\{a_n\}$的公比为q,由题设得2a₁ = a₂ + a₃,
即2a₁ = a₁q + a₁q²。 2分
所以q² + q - 2 = 0,解得q = 1(舍去),q = -2。
故$\{a_n\}$的公比为 -2。 6分
(2)记Sₙ为$\{na_n\}$的前n项和。由
(1)及题设可得,aₙ = (-2)ⁿ⁻¹。
所以Sₙ = 1 + 2×(-2) + … + n×(-2)ⁿ⁻¹,
-2Sₙ = -2 + 2×(-2)² + … + (n - 1)×(-2)ⁿ⁻¹ + n×(-2)ⁿ。 8分
可得3Sₙ = 1 + (-2) + (-2)² + … + (-2)ⁿ⁻¹ - n×(-2)ⁿ
= $\frac{1 - (-2)ⁿ}{3}$ - n×(-2)ⁿ。 11分
所以Sₙ = $\frac{1}{9}$[1 - (3n + 1)(-2)ⁿ]。 12分
[解]
(1)设$\{a_n\}$的公比为q,由题设得2a₁ = a₂ + a₃,
即2a₁ = a₁q + a₁q²。 2分
所以q² + q - 2 = 0,解得q = 1(舍去),q = -2。
故$\{a_n\}$的公比为 -2。 6分
(2)记Sₙ为$\{na_n\}$的前n项和。由
(1)及题设可得,aₙ = (-2)ⁿ⁻¹。
所以Sₙ = 1 + 2×(-2) + … + n×(-2)ⁿ⁻¹,
-2Sₙ = -2 + 2×(-2)² + … + (n - 1)×(-2)ⁿ⁻¹ + n×(-2)ⁿ。 8分
可得3Sₙ = 1 + (-2) + (-2)² + … + (-2)ⁿ⁻¹ - n×(-2)ⁿ
= $\frac{1 - (-2)ⁿ}{3}$ - n×(-2)ⁿ。 11分
所以Sₙ = $\frac{1}{9}$[1 - (3n + 1)(-2)ⁿ]。 12分
18. (本小题满分12分)如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE = AD.△ABC是底面的内接正三角形,P为DO上一点,PO = $\frac{\sqrt{6}}{6}$DO.
(1)证明:PA⊥平面PBC;
(2)求二面角B−PC−E的余弦值.

答案:
18.[命题点]线面垂直关系的判定以及二面角的求法
(1)[证明]设$AB = a$,由题设可得$PO=\frac{\sqrt{6}}{6}a$,$AO=\frac{\sqrt{3}}{3}a$,$AB = a$,$PA = PB = PC=\frac{\sqrt{2}}{2}a$。 2分
因此$PA^{2}+PB^{2}=AB^{2}$,从而$PA\perp PB$。
又$PA^{2}+PC^{2}=AC^{2}$,故$PA\perp PC$。 4分
又$PB\cap PC = P$,所以$PA\perp$平面$PBC$。 5分
(2)[解]解法一:以$O$为坐标原点,$\overrightarrow{OE}$的方向为$y$轴正方向,$\vert OE\vert$为单位长,建立如图所示的空间直角坐标系$O - xyz$。

由题设可得$E(0,1,0)$,$A(0, - 1,0)$,$C(\frac{\sqrt{3}}{2},\frac{1}{2},0)$,$P(0,0,\frac{\sqrt{2}}{2})$。
所以$\overrightarrow{EC}=(\frac{\sqrt{3}}{2},-\frac{1}{2},0)$,$\overrightarrow{EP}=(0, - 1,\frac{\sqrt{2}}{2})$。 6分
设$\boldsymbol{m}=(x,y,z)$是平面$PCE$的法向量,则
$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{EP}=0\\\boldsymbol{m}\cdot\overrightarrow{EC}=0\end{cases}$,即$\begin{cases}-y+\frac{\sqrt{2}}{2}z = 0\\\frac{\sqrt{3}}{2}x-\frac{1}{2}y = 0\end{cases}$,可取$\boldsymbol{m}=(\frac{\sqrt{3}}{3},1,\sqrt{2})$。
8分
由
(1)知$\overrightarrow{AP}=(0,1,\frac{\sqrt{2}}{2})$是平面$PCB$的一个法向量,记$\boldsymbol{n}=\overrightarrow{AP}$。
9分
则$\cos\langle\boldsymbol{n},\boldsymbol{m}\rangle=\frac{\boldsymbol{n}\cdot\boldsymbol{m}}{\vert\boldsymbol{n}\vert\cdot\vert\boldsymbol{m}\vert}=\frac{2\sqrt{5}}{5}$ 11分
所以二面角$B - PC - E$的余弦值为$\frac{2\sqrt{5}}{5}$。 12分
解法二:设$BC\cap AE = F$,易知$F$是$BC$的中点,过$F$作$FG// PA$交$PE$于点$G$,取$PC$的中点$H$,连接$GH$,$HF$,则$HF// PB$。

由$PA\perp$平面$PBC$,得$FG\perp$平面$PBC$。
由
(1)可得$BC^{2}=PB^{2}+PC^{2}$,所以$PB\perp PC$,所以$HF\perp PC$,根据三垂线定理,得$GH\perp PC$,所以$\angle GHF$是二面角$B - PC - E$的平面角。 8分
设圆$O$的半径为$r$,则$AF = AB\sin60^{\circ}=\frac{3}{2}r$,$AE = 2r$,$EF=\frac{1}{2}r$,$\frac{EF}{AF}=\frac{1}{3}$,所以$FG=\frac{1}{3}PA$,$HF=\frac{1}{2}PB=\frac{1}{2}PA$,所以$\frac{FG}{HF}=\frac{1}{2}$
10分
在$Rt\triangle GFH$中,$\tan\angle GHF=\frac{FG}{HF}=\frac{1}{2}$,则$\cos\angle GHF=\frac{2\sqrt{5}}{5}$,
所以二面角$B - PC - E$的余弦值为$\frac{2\sqrt{5}}{5}$。 12分
解法三:如图所示,在$PE$上取点$H$,使$HE=\frac{1}{4}PE$,设$BC\cap AE = N$,连接$NH$。

由
(1)知$NE=\frac{1}{4}AE$,所以$NH// PA$,故$NH\perp$平面$PBC$。
所以点$H$在平面$PBC$上的射影为$N$。
故由射影面积法可知二面角$B - PC - E$的余弦值为$\cos\theta=\frac{S_{\triangle PCN}}{S_{\triangle PCH}}$。
8分
在$\triangle PCE$中,令$PC = PE=\frac{\sqrt{6}}{2}$,则$CE = 1$,易知$S_{\triangle PCE}=\frac{\sqrt{5}}{4}$,所以$S_{\triangle PCH}=\frac{3}{4}S_{\triangle PCE}=\frac{3\sqrt{5}}{16}$ 10分
又$S_{\triangle PCN}=\frac{1}{2}S_{\triangle PBC}=\frac{3}{8}$,故$\cos\theta=\frac{S_{\triangle PCN}}{S_{\triangle PCH}}=\frac{\frac{3}{8}}{\frac{3\sqrt{5}}{16}}=\frac{2\sqrt{5}}{5}$,
16
所以二面角$B - PC - E$的余弦值为$\frac{2\sqrt{5}}{5}$ 12分
18.[命题点]线面垂直关系的判定以及二面角的求法
(1)[证明]设$AB = a$,由题设可得$PO=\frac{\sqrt{6}}{6}a$,$AO=\frac{\sqrt{3}}{3}a$,$AB = a$,$PA = PB = PC=\frac{\sqrt{2}}{2}a$。 2分
因此$PA^{2}+PB^{2}=AB^{2}$,从而$PA\perp PB$。
又$PA^{2}+PC^{2}=AC^{2}$,故$PA\perp PC$。 4分
又$PB\cap PC = P$,所以$PA\perp$平面$PBC$。 5分
(2)[解]解法一:以$O$为坐标原点,$\overrightarrow{OE}$的方向为$y$轴正方向,$\vert OE\vert$为单位长,建立如图所示的空间直角坐标系$O - xyz$。

由题设可得$E(0,1,0)$,$A(0, - 1,0)$,$C(\frac{\sqrt{3}}{2},\frac{1}{2},0)$,$P(0,0,\frac{\sqrt{2}}{2})$。
所以$\overrightarrow{EC}=(\frac{\sqrt{3}}{2},-\frac{1}{2},0)$,$\overrightarrow{EP}=(0, - 1,\frac{\sqrt{2}}{2})$。 6分
设$\boldsymbol{m}=(x,y,z)$是平面$PCE$的法向量,则
$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{EP}=0\\\boldsymbol{m}\cdot\overrightarrow{EC}=0\end{cases}$,即$\begin{cases}-y+\frac{\sqrt{2}}{2}z = 0\\\frac{\sqrt{3}}{2}x-\frac{1}{2}y = 0\end{cases}$,可取$\boldsymbol{m}=(\frac{\sqrt{3}}{3},1,\sqrt{2})$。
8分
由
(1)知$\overrightarrow{AP}=(0,1,\frac{\sqrt{2}}{2})$是平面$PCB$的一个法向量,记$\boldsymbol{n}=\overrightarrow{AP}$。
9分
则$\cos\langle\boldsymbol{n},\boldsymbol{m}\rangle=\frac{\boldsymbol{n}\cdot\boldsymbol{m}}{\vert\boldsymbol{n}\vert\cdot\vert\boldsymbol{m}\vert}=\frac{2\sqrt{5}}{5}$ 11分
所以二面角$B - PC - E$的余弦值为$\frac{2\sqrt{5}}{5}$。 12分
解法二:设$BC\cap AE = F$,易知$F$是$BC$的中点,过$F$作$FG// PA$交$PE$于点$G$,取$PC$的中点$H$,连接$GH$,$HF$,则$HF// PB$。

由$PA\perp$平面$PBC$,得$FG\perp$平面$PBC$。
由
(1)可得$BC^{2}=PB^{2}+PC^{2}$,所以$PB\perp PC$,所以$HF\perp PC$,根据三垂线定理,得$GH\perp PC$,所以$\angle GHF$是二面角$B - PC - E$的平面角。 8分
设圆$O$的半径为$r$,则$AF = AB\sin60^{\circ}=\frac{3}{2}r$,$AE = 2r$,$EF=\frac{1}{2}r$,$\frac{EF}{AF}=\frac{1}{3}$,所以$FG=\frac{1}{3}PA$,$HF=\frac{1}{2}PB=\frac{1}{2}PA$,所以$\frac{FG}{HF}=\frac{1}{2}$
10分
在$Rt\triangle GFH$中,$\tan\angle GHF=\frac{FG}{HF}=\frac{1}{2}$,则$\cos\angle GHF=\frac{2\sqrt{5}}{5}$,
所以二面角$B - PC - E$的余弦值为$\frac{2\sqrt{5}}{5}$。 12分
解法三:如图所示,在$PE$上取点$H$,使$HE=\frac{1}{4}PE$,设$BC\cap AE = N$,连接$NH$。

由
(1)知$NE=\frac{1}{4}AE$,所以$NH// PA$,故$NH\perp$平面$PBC$。
所以点$H$在平面$PBC$上的射影为$N$。
故由射影面积法可知二面角$B - PC - E$的余弦值为$\cos\theta=\frac{S_{\triangle PCN}}{S_{\triangle PCH}}$。
8分
在$\triangle PCE$中,令$PC = PE=\frac{\sqrt{6}}{2}$,则$CE = 1$,易知$S_{\triangle PCE}=\frac{\sqrt{5}}{4}$,所以$S_{\triangle PCH}=\frac{3}{4}S_{\triangle PCE}=\frac{3\sqrt{5}}{16}$ 10分
又$S_{\triangle PCN}=\frac{1}{2}S_{\triangle PBC}=\frac{3}{8}$,故$\cos\theta=\frac{S_{\triangle PCN}}{S_{\triangle PCH}}=\frac{\frac{3}{8}}{\frac{3\sqrt{5}}{16}}=\frac{2\sqrt{5}}{5}$,
16
所以二面角$B - PC - E$的余弦值为$\frac{2\sqrt{5}}{5}$ 12分
19. (本小题满分12分)甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:
累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.
经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为$\frac{1}{2}$.
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
答案:
19.[命题点]相互独立事件、对立事件的概率
[解]
(1)甲连胜四场的概率为$\frac{1}{16}$。 4分
(2)根据赛制,至少需要进行四场比赛,至多需要进行五场比赛。
比赛四场结束,共有三种情况:
甲连胜四场的概率为$\frac{1}{16}$; 5分
乙连胜四场的概率为$\frac{1}{16}$; 6分
丙上场后连胜三场的概率为$\frac{1}{8}$ 7分
所以需要进行第五场比赛的概率为$1-\frac{1}{16}-\frac{1}{16}-\frac{1}{8}=\frac{3}{4}$。
8分
关键点拨
丙上场后连胜三场情形如下:
比赛双方 获胜
第一场 甲 乙 甲(或乙)
第二场 甲(或乙) 丙 丙
第三场 丙 乙(或甲) 丙
第四场 甲(或乙) 丙 丙
所以丙上场后,连胜三场的概率为$\frac{1}{16}\times2=\frac{1}{8}$。
(3)丙最终获胜,有两种情况:
比赛四场结束且丙最终获胜的概率为$\frac{1}{8}$; 9分
比赛五场结束且丙最终获胜,则从第二场开始的四场比赛按照丙的胜、负、轮空结果有三种情况:胜胜负胜,胜负空胜,负空胜胜,概率分别为$\frac{1}{16}$,$\frac{1}{8}$,$\frac{1}{8}$ 11分
因此丙最终获胜的概率为$\frac{1}{8}+\frac{1}{16}+\frac{1}{8}+\frac{1}{8}=\frac{7}{16}$。 12分
一题多解:设事件$M$为甲赢,事件$N$为丙赢,则甲赢的基本事件包括:$BCBC$,$ABCBC$,$ACBCB$,$BABCC$,$BACBC$,$BCACB$,$BCABC$,$BCBAC$,则
4 5
$P(M)=(\frac{1}{2})^{4}+7\times(\frac{1}{2})^{5}=\frac{9}{32}$ 10分
由对称性可知乙赢和甲赢概率相等,所以$P(N)=1 - 2\times\frac{9}{32}=\frac{7}{16}$ 12分
[解]
(1)甲连胜四场的概率为$\frac{1}{16}$。 4分
(2)根据赛制,至少需要进行四场比赛,至多需要进行五场比赛。
比赛四场结束,共有三种情况:
甲连胜四场的概率为$\frac{1}{16}$; 5分
乙连胜四场的概率为$\frac{1}{16}$; 6分
丙上场后连胜三场的概率为$\frac{1}{8}$ 7分
所以需要进行第五场比赛的概率为$1-\frac{1}{16}-\frac{1}{16}-\frac{1}{8}=\frac{3}{4}$。
8分
关键点拨
丙上场后连胜三场情形如下:
比赛双方 获胜
第一场 甲 乙 甲(或乙)
第二场 甲(或乙) 丙 丙
第三场 丙 乙(或甲) 丙
第四场 甲(或乙) 丙 丙
所以丙上场后,连胜三场的概率为$\frac{1}{16}\times2=\frac{1}{8}$。
(3)丙最终获胜,有两种情况:
比赛四场结束且丙最终获胜的概率为$\frac{1}{8}$; 9分
比赛五场结束且丙最终获胜,则从第二场开始的四场比赛按照丙的胜、负、轮空结果有三种情况:胜胜负胜,胜负空胜,负空胜胜,概率分别为$\frac{1}{16}$,$\frac{1}{8}$,$\frac{1}{8}$ 11分
因此丙最终获胜的概率为$\frac{1}{8}+\frac{1}{16}+\frac{1}{8}+\frac{1}{8}=\frac{7}{16}$。 12分
一题多解:设事件$M$为甲赢,事件$N$为丙赢,则甲赢的基本事件包括:$BCBC$,$ABCBC$,$ACBCB$,$BABCC$,$BACBC$,$BCACB$,$BCABC$,$BCBAC$,则
4 5
$P(M)=(\frac{1}{2})^{4}+7\times(\frac{1}{2})^{5}=\frac{9}{32}$ 10分
由对称性可知乙赢和甲赢概率相等,所以$P(N)=1 - 2\times\frac{9}{32}=\frac{7}{16}$ 12分
查看更多完整答案,请扫码查看


