2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 设全集U = {−2, −1, 0, 1, 2},集合A = {0, 1, 2},B = {−1, 2},则A∩(∁UB) = ( )
A. {0, 1}
B. {0, 1, 2}
C. {−1, 1, 2}
D. {−1, 0, 1, 2}
A. {0, 1}
B. {0, 1, 2}
C. {−1, 1, 2}
D. {−1, 0, 1, 2}
答案:
1. A [命题点]集合的交集、补集运算
[深度解析]由题意知$\complement_{U}B = \{ - 2,0,1\}$,则$A\cap(\complement_{U}B) = \{ 0,1\}$,故选A.
[深度解析]由题意知$\complement_{U}B = \{ - 2,0,1\}$,则$A\cap(\complement_{U}B) = \{ 0,1\}$,故选A.
2. “x为整数”是“2x + 1为整数”的 ( )
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
答案:
2. A [命题点]充分、必要条件的判断
[深度解析]由题意知“x为整数”可推出“2x + 1为整数”,故充分性成立;反之不成立,如,当$x = \frac{1}{2}$时,2x + 1为整数,x不是整数(提示:特殊值法),故必要性不成立.所以“x为整数”是“2x + 1为整数”的充分不必要条件,故选A.
[深度解析]由题意知“x为整数”可推出“2x + 1为整数”,故充分性成立;反之不成立,如,当$x = \frac{1}{2}$时,2x + 1为整数,x不是整数(提示:特殊值法),故必要性不成立.所以“x为整数”是“2x + 1为整数”的充分不必要条件,故选A.
3. 函数y = $\frac{|x² - 1|}{x}$的图像大致为 ( )
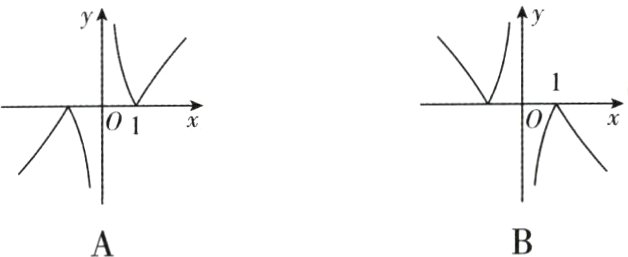



答案:
3. A [命题点]函数图像的识别
[深度解析]因为函数$f(x)$的定义域为$(-\infty,0)\cup(0,+\infty)$,且$f(-x)=\frac{|x^{2}-1|}{-x}=-f(x)$,所以函数$f(x)$为奇函数,图像关于原点对称,所以排除C,D;当$x\lt0$时,$f(x)\lt0$,所以排除B,故选A.快解:只有A满足题意,故选A.
方法速记:特殊值排除.
[深度解析]因为函数$f(x)$的定义域为$(-\infty,0)\cup(0,+\infty)$,且$f(-x)=\frac{|x^{2}-1|}{-x}=-f(x)$,所以函数$f(x)$为奇函数,图像关于原点对称,所以排除C,D;当$x\lt0$时,$f(x)\lt0$,所以排除B,故选A.快解:只有A满足题意,故选A.
方法速记:特殊值排除.
4. 将1916年到2015年的全球年平均气温(单位:℃),共100个数据,分成6组:[13.55, 13.75),[13.75, 13.95),[13.95, 14.15),[14.15, 14.35),[14.35, 14.55),[14.55, 14.75],并整理得到如下的频率分布直方图,则全球年平均气温在区间[14.35, 14.75]内的有 ( )

13.55 13.75 13.95 14.15 14.35 14.55 14.75全球年平均气温/℃
A. 22年
B. 23年
C. 25年
D. 35年
答案:
4. B [命题点]频率分布直方图的应用
[深度解析]依题意,全球年平均气温在区间$[14.35,14.75]$内的频率是$0.2\times0.5 + 0.2\times0.65 = 0.23$,故全球年平均气温在区间$[14.35,14.75]$内的有$100\times0.23 = 23$年.故选B.
[深度解析]依题意,全球年平均气温在区间$[14.35,14.75]$内的频率是$0.2\times0.5 + 0.2\times0.65 = 0.23$,故全球年平均气温在区间$[14.35,14.75]$内的有$100\times0.23 = 23$年.故选B.
5. 设a = 2⁰.⁷,b = ($\frac{1}{3}$)⁰.⁷,c = log₂$\frac{1}{3}$,则a,b,c的大小关系为 ( )
A. a<b<c
B. c<a<b
C. b<c<a
D. c<b<a
A. a<b<c
B. c<a<b
C. b<c<a
D. c<b<a
答案:
5. D [命题点]利用指数、对数函数的单调性比较大小
[深度解析]由题意知,$a = 2^{0.7}\gt2^{0}=1$,$b = (\frac{1}{3})^{0.7}=3^{-0.7}\lt3^{0}=1$,又$b\gt0$,所以$0\lt b\lt1$,$c = \log_{2}\frac{1}{3}\lt0$,所以$c\lt b\lt a$.故选D.
方法速记:①同底的指数、对数式可以利用指数或对数函数的单调性比较大小;②不同底的指数、对数式,先看是否能化成同底,如不能,则可借助于中间值0,1等比较大小
[深度解析]由题意知,$a = 2^{0.7}\gt2^{0}=1$,$b = (\frac{1}{3})^{0.7}=3^{-0.7}\lt3^{0}=1$,又$b\gt0$,所以$0\lt b\lt1$,$c = \log_{2}\frac{1}{3}\lt0$,所以$c\lt b\lt a$.故选D.
方法速记:①同底的指数、对数式可以利用指数或对数函数的单调性比较大小;②不同底的指数、对数式,先看是否能化成同底,如不能,则可借助于中间值0,1等比较大小
6.化简(2log₄3 + log₈3)(log₃2 + log₉2) = ( )
A.1 B.$\frac{5}{4}$ C.2 D.$\frac{5}{2}$
A.1 B.$\frac{5}{4}$ C.2 D.$\frac{5}{2}$
答案:
6.C[命题点]对数的化简运算.
[深度解析]原式=(2log₂3 + log₃3)(log₃2 + log₃2²)
=(2×$\frac{1}{2}$log₂3 + $\frac{1}{3}$log₃3)(log₃2 + $\frac{1}{2}$log₃2)
=$\frac{4}{3}$log₂3×$\frac{3}{2}$log₃2
=2.故选C.
[深度解析]原式=(2log₂3 + log₃3)(log₃2 + log₃2²)
=(2×$\frac{1}{2}$log₂3 + $\frac{1}{3}$log₃3)(log₃2 + $\frac{1}{2}$log₃2)
=$\frac{4}{3}$log₂3×$\frac{3}{2}$log₃2
=2.故选C.
7.已知双曲线$\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ (a>0,b>1)的左、右焦点分别为F₁,F₂,抛物线y² = 4√5x的准线l经过F₁,且l与双曲线的一条渐近线交于点A。若∠F₁F₂A = $\frac{\pi}{4}$,则双曲线的方程为 ( )
A.$\frac{x^{2}}{16} - \frac{y^{2}}{4} = 1$ B.$\frac{x^{2}}{4} - \frac{y^{2}}{16} = 1$
C.$\frac{x^{2}}{4} - y^{2} = 1$ D.x² - $\frac{y^{2}}{4} = 1$
A.$\frac{x^{2}}{16} - \frac{y^{2}}{4} = 1$ B.$\frac{x^{2}}{4} - \frac{y^{2}}{16} = 1$
C.$\frac{x^{2}}{4} - y^{2} = 1$ D.x² - $\frac{y^{2}}{4} = 1$
答案:
7.D [命题点]双曲线的标准方程和几何性质、抛物线的定义
[深度解析]由题可知,抛物线y² = 4$\sqrt{5}$x的准线l的方程为x = -$\sqrt{5}$,双曲线左焦点坐标F( - c,0).又准线l过双曲线的焦点F₁,所以c = $\sqrt{5}$①.不妨取双曲线的一条渐近线方程为y = $\frac{b}{a}$x,则A( - c,$\frac{bc}{a}$).又因为∠F₁FA = $\frac{\pi}{4}$,所以|AF₁| = |FF₂|,即$\frac{bc}{a}$ = 2c,可得$\frac{b}{a}$ = 2②.
由①②结合a² + b² = c²,可得a² = 1,b² = 4,所以双曲线的标准方程为x² - $\frac{y²}{4}$ = 1,故选D.

7.D [命题点]双曲线的标准方程和几何性质、抛物线的定义
[深度解析]由题可知,抛物线y² = 4$\sqrt{5}$x的准线l的方程为x = -$\sqrt{5}$,双曲线左焦点坐标F( - c,0).又准线l过双曲线的焦点F₁,所以c = $\sqrt{5}$①.不妨取双曲线的一条渐近线方程为y = $\frac{b}{a}$x,则A( - c,$\frac{bc}{a}$).又因为∠F₁FA = $\frac{\pi}{4}$,所以|AF₁| = |FF₂|,即$\frac{bc}{a}$ = 2c,可得$\frac{b}{a}$ = 2②.
由①②结合a² + b² = c²,可得a² = 1,b² = 4,所以双曲线的标准方程为x² - $\frac{y²}{4}$ = 1,故选D.

8.十字歇山顶是中国古代建筑屋顶的经典样式之一,图1中的故宫角楼的顶部即为十字歇山顶。其上部可视为由两个相同的直三棱柱交叠而成的几何体(图2)。这两个直三棱柱有一个公共侧面ABCD。在底面BCE中,若BE = CE = 3,∠BEC = 120°,则该几何体的体积为 ( )

A.$\frac{27}{2}$ B.$\frac{27\sqrt{3}}{2}$ C.27 D.27$\sqrt{3}$

A.$\frac{27}{2}$ B.$\frac{27\sqrt{3}}{2}$ C.27 D.27$\sqrt{3}$
答案:
8.C [命题点]空间几何体体积的计算
[深度解析]由题图可得两直三棱柱BCE - ADF,ABM - DCN重叠后的图形如图所示,在△BCE中,由BE = CE = 3,∠BEC = 120°,可得BC = 3$\sqrt{3}$,所以正方形ABCD的边长为3$\sqrt{3}$.又因为三棱柱BCE - ADF是直三棱柱,所以VBCE - ADF = S△BCE·AB = $\frac{1}{2}$×3×3×sin120°×3$\sqrt{3}$ = $\frac{81}{4}$.由对称性可知,S为棱MN的中点,所以VS - ABM = VS - DCN = $\frac{1}{3}$S△ABM·SM = $\frac{1}{3}$×$\frac{1}{2}$×3×3×sin120°×$\frac{3\sqrt{3}}{2}$ = $\frac{27}{8}$.所以该几何体的体积V = VBCE - ADF + VS - ABM + VS - DCN = $\frac{81}{4}$ + $\frac{27}{8}$ + $\frac{27}{8}$ = 27,故选C.
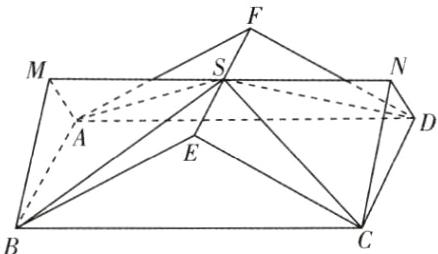
8.C [命题点]空间几何体体积的计算
[深度解析]由题图可得两直三棱柱BCE - ADF,ABM - DCN重叠后的图形如图所示,在△BCE中,由BE = CE = 3,∠BEC = 120°,可得BC = 3$\sqrt{3}$,所以正方形ABCD的边长为3$\sqrt{3}$.又因为三棱柱BCE - ADF是直三棱柱,所以VBCE - ADF = S△BCE·AB = $\frac{1}{2}$×3×3×sin120°×3$\sqrt{3}$ = $\frac{81}{4}$.由对称性可知,S为棱MN的中点,所以VS - ABM = VS - DCN = $\frac{1}{3}$S△ABM·SM = $\frac{1}{3}$×$\frac{1}{2}$×3×3×sin120°×$\frac{3\sqrt{3}}{2}$ = $\frac{27}{8}$.所以该几何体的体积V = VBCE - ADF + VS - ABM + VS - DCN = $\frac{81}{4}$ + $\frac{27}{8}$ + $\frac{27}{8}$ = 27,故选C.

9.关于函数$f(x) = \frac{1}{2}\sin2x$,给出下列结论:
①$f(x)$的最小正周期是2π;
②$f(x)$在区间[$-\frac{\pi}{4}$,$\frac{\pi}{4}$]上单调递增;
③当x∈[$-\frac{\pi}{6}$,$\frac{\pi}{3}$]时,$f(x)$的取值范围为[$-\frac{\sqrt{3}}{4}$,$\frac{\sqrt{3}}{4}$];
④$f(x)$的图像可以由函数$g(x) = \frac{1}{2}\sin(2x + \varphi)$的图像向左平移$\frac{\pi}{?}$单位长度得到。
其中正确结论的个数为 ( )
A.1 B.2 C.3 D.4
①$f(x)$的最小正周期是2π;
②$f(x)$在区间[$-\frac{\pi}{4}$,$\frac{\pi}{4}$]上单调递增;
③当x∈[$-\frac{\pi}{6}$,$\frac{\pi}{3}$]时,$f(x)$的取值范围为[$-\frac{\sqrt{3}}{4}$,$\frac{\sqrt{3}}{4}$];
④$f(x)$的图像可以由函数$g(x) = \frac{1}{2}\sin(2x + \varphi)$的图像向左平移$\frac{\pi}{?}$单位长度得到。
其中正确结论的个数为 ( )
A.1 B.2 C.3 D.4
答案:
9.A [命题点]三角函数的图像与性质、三角函数图像的平移变换
[深度解析]①函数f(x) = $\frac{1}{2}$sin2x的最小正周期是$\frac{2\pi}{2}$ = π,所以结论错误;②令z = 2x,当x∈[ - $\frac{\pi}{4}$,$\frac{\pi}{4}$]时,z∈[ - $\frac{\pi}{2}$,$\frac{\pi}{2}$],而函数y = $\frac{1}{2}$sinz在[ - $\frac{\pi}{2}$,$\frac{\pi}{2}$]上单调递增,所以结论正确;
③当x∈[ - $\frac{\pi}{6}$,$\frac{\pi}{3}$]时,2x∈[ - $\frac{\pi}{3}$,$\frac{2\pi}{3}$],sin2x∈[ - $\frac{\sqrt{3}}{2}$,1],$\frac{1}{2}$sin2x∈[ - $\frac{\sqrt{3}}{4}$,$\frac{1}{2}$],从而f(x)的取值范围为[ - $\frac{\sqrt{3}}{4}$,$\frac{1}{2}$],所以结论错误;④函数g(x) = $\frac{1}{2}$sin(2x + $\frac{\pi}{4}$)的图像向左平移$\frac{\pi}{8}$个单位长度得到函数y = $\frac{1}{2}$sin[2(x + $\frac{\pi}{8}$) + $\frac{\pi}{4}$] = $\frac{1}{2}$sin(2x + $\frac{\pi}{2}$) = $\frac{1}{2}$cos2x的图像,所以结论错误.综上所述,正确结论的个数为1.故选A.
[深度解析]①函数f(x) = $\frac{1}{2}$sin2x的最小正周期是$\frac{2\pi}{2}$ = π,所以结论错误;②令z = 2x,当x∈[ - $\frac{\pi}{4}$,$\frac{\pi}{4}$]时,z∈[ - $\frac{\pi}{2}$,$\frac{\pi}{2}$],而函数y = $\frac{1}{2}$sinz在[ - $\frac{\pi}{2}$,$\frac{\pi}{2}$]上单调递增,所以结论正确;
③当x∈[ - $\frac{\pi}{6}$,$\frac{\pi}{3}$]时,2x∈[ - $\frac{\pi}{3}$,$\frac{2\pi}{3}$],sin2x∈[ - $\frac{\sqrt{3}}{2}$,1],$\frac{1}{2}$sin2x∈[ - $\frac{\sqrt{3}}{4}$,$\frac{1}{2}$],从而f(x)的取值范围为[ - $\frac{\sqrt{3}}{4}$,$\frac{1}{2}$],所以结论错误;④函数g(x) = $\frac{1}{2}$sin(2x + $\frac{\pi}{4}$)的图像向左平移$\frac{\pi}{8}$个单位长度得到函数y = $\frac{1}{2}$sin[2(x + $\frac{\pi}{8}$) + $\frac{\pi}{4}$] = $\frac{1}{2}$sin(2x + $\frac{\pi}{2}$) = $\frac{1}{2}$cos2x的图像,所以结论错误.综上所述,正确结论的个数为1.故选A.
查看更多完整答案,请扫码查看


