2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 已知集合$M = \{ - 2, - 1,0,1,2\}$,$N = \{ x|x^2 - x - 6\geq0\}$,则$M\cap N =$ ( )
A. $\{ - 2, - 1,0,1\}$
B. $\{ 0,1,2\}$
C. $\{ - 2\}$
D. $\{ 2\}$
A. $\{ - 2, - 1,0,1\}$
B. $\{ 0,1,2\}$
C. $\{ - 2\}$
D. $\{ 2\}$
答案:
1.C [命题点]一元二次不等式的解法及集合的交集运算
[深度解析]由x²−x−6≥0,得x≤−2或x≥3,则N={x|x≤−2或x≥3}。
∵M={−2,−1,0,1,2},
∴M∩N={−2},故选C。
[深度解析]由x²−x−6≥0,得x≤−2或x≥3,则N={x|x≤−2或x≥3}。
∵M={−2,−1,0,1,2},
∴M∩N={−2},故选C。
2. 已知$z = \frac{1 - i}{2 + 2i}$,则$z - \overline{z} =$ ( )
A. $-i$
B. $i$
C. $0$
D. $1$
A. $-i$
B. $i$
C. $0$
D. $1$
答案:
2.A [命题点]复数的四则运算及共轭复数的概念
[深度解析]z=$\frac{1 - i}{2 + 2i}$=$\frac{(1 - i)^2}{2(1 + i)(1 - i)}$=$\frac{-2i}{4}$=$-\frac{1}{2}i$,则$\overline{z}$=$\frac{1}{2}i$,
∴z - $\overline{z}$=$-\frac{1}{2}i - \frac{1}{2}i$= - i,故选A。
[深度解析]z=$\frac{1 - i}{2 + 2i}$=$\frac{(1 - i)^2}{2(1 + i)(1 - i)}$=$\frac{-2i}{4}$=$-\frac{1}{2}i$,则$\overline{z}$=$\frac{1}{2}i$,
∴z - $\overline{z}$=$-\frac{1}{2}i - \frac{1}{2}i$= - i,故选A。
3. 已知向量$\vec{a} = (1,1)$,$\vec{b} = (1, - 1)$。若$(\vec{a}+\lambda\vec{b})\perp(\vec{a}+\mu\vec{b})$,则 ( )
A. $\lambda+\mu = 1$
B. $\lambda+\mu = - 1$
C. $\lambda\mu = 1$
D. $\lambda\mu = - 1$
A. $\lambda+\mu = 1$
B. $\lambda+\mu = - 1$
C. $\lambda\mu = 1$
D. $\lambda\mu = - 1$
答案:
3.D [命题点]平面向量的坐标运算及垂直
[深度解析]由于$\vec{a}$=(1,1),$\vec{b}$=(1, - 1),则$\vec{a}$ + λ$\vec{b}$=(1,1)+(λ, - λ)=(1 + λ,1 - λ),$\vec{a}$ + μ$\vec{b}$=(1,1)+μ(1, - 1)=(1 + μ,1 - μ)。
又
∵($\vec{a}$ + λ$\vec{b}$)⊥($\vec{a}$ + μ$\vec{b}$),
∴($\vec{a}$ + λ$\vec{b}$)·($\vec{a}$ + μ$\vec{b}$)=0,即(1 + λ)(1 + μ)+(1 - λ)(1 - μ)=0,解得λμ = - 1,故选D。
[深度解析]由于$\vec{a}$=(1,1),$\vec{b}$=(1, - 1),则$\vec{a}$ + λ$\vec{b}$=(1,1)+(λ, - λ)=(1 + λ,1 - λ),$\vec{a}$ + μ$\vec{b}$=(1,1)+μ(1, - 1)=(1 + μ,1 - μ)。
又
∵($\vec{a}$ + λ$\vec{b}$)⊥($\vec{a}$ + μ$\vec{b}$),
∴($\vec{a}$ + λ$\vec{b}$)·($\vec{a}$ + μ$\vec{b}$)=0,即(1 + λ)(1 + μ)+(1 - λ)(1 - μ)=0,解得λμ = - 1,故选D。
4. 设函数$f(x) = 2\cos(x - \alpha)$在区间$(0,1)$单调递减,则$\alpha$的取值范围是 ( )
A. $(-\infty, - 2]$
B. $[ - 2,0)$
C. $(0,2]$
D. $[2, +\infty)$
A. $(-\infty, - 2]$
B. $[ - 2,0)$
C. $(0,2]$
D. $[2, +\infty)$
答案:
4.D [命题点]复合函数的单调性
[深度解析]因为y = 2^x在R上是增函数,所以函数y = x(x - 2)=x² - 2x=(x - 1)² - 1在(0,1)上单调递减(提示:复合函数的单调性遵循“同增异减”原则),所以对称轴x = 1≤$\frac{a}{2}$,解得a≥2,即a的取值范围是[2,+∞),故选D。
[深度解析]因为y = 2^x在R上是增函数,所以函数y = x(x - 2)=x² - 2x=(x - 1)² - 1在(0,1)上单调递减(提示:复合函数的单调性遵循“同增异减”原则),所以对称轴x = 1≤$\frac{a}{2}$,解得a≥2,即a的取值范围是[2,+∞),故选D。
5. 设椭圆$C_1:\frac{x^2}{a^2}+y^2 = 1(a\gt1)$,$C_2:\frac{x^2}{4}+y^2 = 1$的离心率分别为$e_1$,$e_2$。若$e_2 = \sqrt{3}e_1$,则$a =$ ( )
A. $\frac{\sqrt{3}}{3}$
B. $\sqrt{2}$
C. $\sqrt{3}$
D. $\sqrt{6}$
A. $\frac{\sqrt{3}}{3}$
B. $\sqrt{2}$
C. $\sqrt{3}$
D. $\sqrt{6}$
答案:
5.A [命题点]椭圆的离心率
[深度解析]由椭圆C的方程知离心率e₁=$\frac{\sqrt{a² - 1}}{a}$,由椭圆C的方程知e₂=$\frac{\sqrt{3}}{2}$。又
∵e₂ = $\sqrt{3}$e₁,即$\frac{\sqrt{3}}{2}$ = $\sqrt{3}$$\frac{\sqrt{a² - 1}}{a}$,化简得a² = 4a² - 4,
∴a² = $\frac{4}{3}$。
∵a>1,
∴a = $\frac{2\sqrt{3}}{3}$。故选A。
[深度解析]由椭圆C的方程知离心率e₁=$\frac{\sqrt{a² - 1}}{a}$,由椭圆C的方程知e₂=$\frac{\sqrt{3}}{2}$。又
∵e₂ = $\sqrt{3}$e₁,即$\frac{\sqrt{3}}{2}$ = $\sqrt{3}$$\frac{\sqrt{a² - 1}}{a}$,化简得a² = 4a² - 4,
∴a² = $\frac{4}{3}$。
∵a>1,
∴a = $\frac{2\sqrt{3}}{3}$。故选A。
6. 过点(0,−2)与圆$x² + y² - 4x - 1 = 0$相切的两条直线的夹角为$\alpha$,则$\sin\alpha =$ ( )
A. 1
B. $\frac{\sqrt{15}}{4}$
C. $\frac{\sqrt{10}}{4}$
D. $\frac{\sqrt{6}}{4}$
A. 1
B. $\frac{\sqrt{15}}{4}$
C. $\frac{\sqrt{10}}{4}$
D. $\frac{\sqrt{6}}{4}$
答案:
6.B [命题点]直线与圆相切、二倍角的正弦公式
[深度解析]设圆x² + y² - 4x - 1 = 0为圆C,化简得(x - 2)² + y² = 5,圆心为C(2,0),半径r = $\sqrt{5}$。如图,
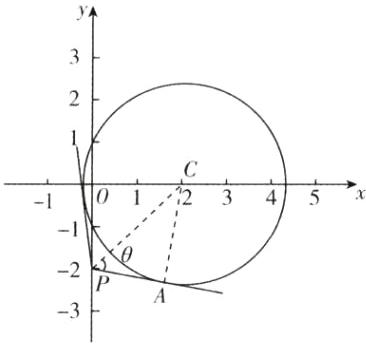
设∠CPA = θ,则α = 2θ,sinθ = $\frac{|CA|}{|CP|}$ = $\frac{\sqrt{5}}{\sqrt{(2 - 0)² + [0 - (-2)]²}}$ = $\frac{\sqrt{5}}{2\sqrt{2}}$,易知cosθ>0,则cosθ = $\frac{\sqrt{3}}{2\sqrt{2}}$,所以sinα = sin2θ = 2sinθcosθ = $\frac{\sqrt{15}}{4}$。故选B。
6.B [命题点]直线与圆相切、二倍角的正弦公式
[深度解析]设圆x² + y² - 4x - 1 = 0为圆C,化简得(x - 2)² + y² = 5,圆心为C(2,0),半径r = $\sqrt{5}$。如图,

设∠CPA = θ,则α = 2θ,sinθ = $\frac{|CA|}{|CP|}$ = $\frac{\sqrt{5}}{\sqrt{(2 - 0)² + [0 - (-2)]²}}$ = $\frac{\sqrt{5}}{2\sqrt{2}}$,易知cosθ>0,则cosθ = $\frac{\sqrt{3}}{2\sqrt{2}}$,所以sinα = sin2θ = 2sinθcosθ = $\frac{\sqrt{15}}{4}$。故选B。
7. 记$S_{n}$为数列$\{a_{n}\}$的前$n$项和,设甲:$\{a_{n}\}$为等差数列;乙:$\{\frac{S_{n}}{n}\}$为等差数列,则 ( )
A. 甲是乙的充分条件但不是必要条件
B. 甲是乙的必要条件但不是充分条件
C. 甲是乙的充要条件
D. 甲既不是乙的充分条件也不是乙的必要条件
A. 甲是乙的充分条件但不是必要条件
B. 甲是乙的必要条件但不是充分条件
C. 甲是乙的充要条件
D. 甲既不是乙的充分条件也不是乙的必要条件
答案:
7.C [命题点]等差数列的判断,充分、必要条件的判断
[深度解析]充分性:若数列{aₙ}为等差数列,设其公差为d(常数),则Sₙ = na₁ + $\frac{n(n - 1)}{2}$d,
∴$\frac{Sₙ}{n}$ = a₁ + $\frac{n - 1}{2}$d,则$\frac{S_{n + 1}}{n + 1}$ - $\frac{Sₙ}{n}$ = (a₁ + $\frac{n}{2}$d) - (a₁ + $\frac{n - 1}{2}$d) = $\frac{d}{2}$(常数),故数列{$\frac{Sₙ}{n}$}是首项为a₁,公差为$\frac{d}{2}$的等差数列,充分性成立;
必要性:若数列{$\frac{Sₙ}{n}$}为等差数列,设其公差为d'(常数),则$\frac{Sₙ}{n}$ = $\frac{S₁}{1}$ + (n - 1)d',当n = 1时,$\frac{S₁}{1}$ = a₁,
∴Sₙ = na₁ + n(n - 1)d',当n ≥ 2时,aₙ = Sₙ - Sₙ₋₁ = [na₁ + n(n - 1)d'] - [(n - 1)a₁ + (n - 1)(n - 2)d'] = a₁ + 2(n - 1)d',当n = 1时,a₁符合上式,显然数列{aₙ}是首项为a₁,公差为2d'的等差数列,因此必要性成立。故甲是乙的充要条件。故选C。
一题多解
充分性:若数列{aₙ}为等差数列,设其公差为d(常数),则aₙ₊₁ - aₙ = d,Sₙ = $\frac{n(a₁ + aₙ)}{2}$,故$\frac{Sₙ}{n}$ = $\frac{a₁ + aₙ}{2}$,
∴$\frac{S_{n + 1}}{n + 1}$ - $\frac{Sₙ}{n}$ = $\frac{a₁ + a_{n + 1}}{2}$ - $\frac{a₁ + aₙ}{2}$ = $\frac{d}{2}$(常数),故数列{$\frac{Sₙ}{n}$}是首项为a₁,公差为$\frac{d}{2}$的等差数列,充分性成立;
必要性:若数列{$\frac{Sₙ}{n}$}为等差数列,则$\frac{S_{n + 1}}{n + 1}$ - $\frac{Sₙ}{n}$ = $\frac{nS_{n + 1} - (n + 1)Sₙ}{n(n + 1)}$ = $\frac{na_{n + 1} - Sₙ}{n(n + 1)}$为常数,设$\frac{na_{n + 1} - Sₙ}{n(n + 1)}$ = t(t为常数),
则Sₙ = naₙ₊₁ - tn(n + 1),当n ≥ 2时,Sₙ₋₁ = (n - 1)aₙ - tn(n - 1),
则aₙ = Sₙ - Sₙ₋₁ = naₙ₊₁ - (n - 1)aₙ - 2tn,整理可得aₙ₊₁ - aₙ = 2t,当n = 1时上式也成立,故数列{aₙ}为等差数列,必要性成立。故甲是乙的充要条件。故选C。
[深度解析]充分性:若数列{aₙ}为等差数列,设其公差为d(常数),则Sₙ = na₁ + $\frac{n(n - 1)}{2}$d,
∴$\frac{Sₙ}{n}$ = a₁ + $\frac{n - 1}{2}$d,则$\frac{S_{n + 1}}{n + 1}$ - $\frac{Sₙ}{n}$ = (a₁ + $\frac{n}{2}$d) - (a₁ + $\frac{n - 1}{2}$d) = $\frac{d}{2}$(常数),故数列{$\frac{Sₙ}{n}$}是首项为a₁,公差为$\frac{d}{2}$的等差数列,充分性成立;
必要性:若数列{$\frac{Sₙ}{n}$}为等差数列,设其公差为d'(常数),则$\frac{Sₙ}{n}$ = $\frac{S₁}{1}$ + (n - 1)d',当n = 1时,$\frac{S₁}{1}$ = a₁,
∴Sₙ = na₁ + n(n - 1)d',当n ≥ 2时,aₙ = Sₙ - Sₙ₋₁ = [na₁ + n(n - 1)d'] - [(n - 1)a₁ + (n - 1)(n - 2)d'] = a₁ + 2(n - 1)d',当n = 1时,a₁符合上式,显然数列{aₙ}是首项为a₁,公差为2d'的等差数列,因此必要性成立。故甲是乙的充要条件。故选C。
一题多解
充分性:若数列{aₙ}为等差数列,设其公差为d(常数),则aₙ₊₁ - aₙ = d,Sₙ = $\frac{n(a₁ + aₙ)}{2}$,故$\frac{Sₙ}{n}$ = $\frac{a₁ + aₙ}{2}$,
∴$\frac{S_{n + 1}}{n + 1}$ - $\frac{Sₙ}{n}$ = $\frac{a₁ + a_{n + 1}}{2}$ - $\frac{a₁ + aₙ}{2}$ = $\frac{d}{2}$(常数),故数列{$\frac{Sₙ}{n}$}是首项为a₁,公差为$\frac{d}{2}$的等差数列,充分性成立;
必要性:若数列{$\frac{Sₙ}{n}$}为等差数列,则$\frac{S_{n + 1}}{n + 1}$ - $\frac{Sₙ}{n}$ = $\frac{nS_{n + 1} - (n + 1)Sₙ}{n(n + 1)}$ = $\frac{na_{n + 1} - Sₙ}{n(n + 1)}$为常数,设$\frac{na_{n + 1} - Sₙ}{n(n + 1)}$ = t(t为常数),
则Sₙ = naₙ₊₁ - tn(n + 1),当n ≥ 2时,Sₙ₋₁ = (n - 1)aₙ - tn(n - 1),
则aₙ = Sₙ - Sₙ₋₁ = naₙ₊₁ - (n - 1)aₙ - 2tn,整理可得aₙ₊₁ - aₙ = 2t,当n = 1时上式也成立,故数列{aₙ}为等差数列,必要性成立。故甲是乙的充要条件。故选C。
8. 已知$\sin(\alpha - \beta) = \frac{1}{3}$,$\cos\alpha\sin\beta = \frac{1}{6}$,则$\cos(2\alpha + 2\beta) =$
( )
A. $\frac{7}{9}$
B. $\frac{1}{9}$
C. $-\frac{1}{9}$
D. $-\frac{7}{9}$
( )
A. $\frac{7}{9}$
B. $\frac{1}{9}$
C. $-\frac{1}{9}$
D. $-\frac{7}{9}$
答案:
8.B
思路导引
sin(α - β) = $\frac{1}{3}$,cosαsinβ = $\frac{1}{6}$→求sinαcosβ的值→求sin(α + β)的值→用二倍角公式求cos(2α + 2β)的值
[命题点]两角和与差的正弦公式及二倍角的余弦公式
[深度解析]
∵sin(α - β) = sinα×cosβ - cosαsinβ = $\frac{1}{3}$,cosαsinβ = $\frac{1}{6}$,
∴sinαcosβ = $\frac{1}{3}$ + cosαsinβ = $\frac{1}{3}$ + $\frac{1}{6}$ = $\frac{1}{2}$
∴sin(α + β) = sinαcosβ + cosαsinβ = $\frac{1}{2}$ + $\frac{1}{6}$ = $\frac{2}{3}$,
∴cos(2α + 2β) = cos[2(α + β)] = 1 - 2sin²(α + β) = 1 - 2×($\frac{2}{3}$)² = $\frac{1}{9}$,故选B。
思路导引
sin(α - β) = $\frac{1}{3}$,cosαsinβ = $\frac{1}{6}$→求sinαcosβ的值→求sin(α + β)的值→用二倍角公式求cos(2α + 2β)的值
[命题点]两角和与差的正弦公式及二倍角的余弦公式
[深度解析]
∵sin(α - β) = sinα×cosβ - cosαsinβ = $\frac{1}{3}$,cosαsinβ = $\frac{1}{6}$,
∴sinαcosβ = $\frac{1}{3}$ + cosαsinβ = $\frac{1}{3}$ + $\frac{1}{6}$ = $\frac{1}{2}$
∴sin(α + β) = sinαcosβ + cosαsinβ = $\frac{1}{2}$ + $\frac{1}{6}$ = $\frac{2}{3}$,
∴cos(2α + 2β) = cos[2(α + β)] = 1 - 2sin²(α + β) = 1 - 2×($\frac{2}{3}$)² = $\frac{1}{9}$,故选B。
9. 有一组样本数据$x_{1},x_{2},\cdots,x_{6}$,其中$x_{1}$是最小值,$x_{6}$是最大值,则 ( )
A. $x_{2},x_{3},x_{4},x_{5}$的平均数等于$x_{1},x_{2},\cdots,x_{6}$的平均数
B. $x_{2},x_{3},x_{4},x_{5}$的中位数等于$x_{1},x_{2},\cdots,x_{6}$的中位数
C. $x_{2},x_{3},x_{4},x_{5}$的标准差不小于$x_{1},x_{2},\cdots,x_{6}$的标准差
D. $x_{2},x_{3},x_{4},x_{5}$的极差不大于$x_{1},x_{2},\cdots,x_{6}$的极差
A. $x_{2},x_{3},x_{4},x_{5}$的平均数等于$x_{1},x_{2},\cdots,x_{6}$的平均数
B. $x_{2},x_{3},x_{4},x_{5}$的中位数等于$x_{1},x_{2},\cdots,x_{6}$的中位数
C. $x_{2},x_{3},x_{4},x_{5}$的标准差不小于$x_{1},x_{2},\cdots,x_{6}$的标准差
D. $x_{2},x_{3},x_{4},x_{5}$的极差不大于$x_{1},x_{2},\cdots,x_{6}$的极差
答案:
9.BD [命题点]样本的数据特征
[深度解析]对于选项A:
∵x₁,x₆不确定,
∴x₁,x₂,…,x₆的平均数不确定,如1,2,2,2,2,4的平均数不等于2,2,2,2的平均数,故A错误;
对于选项B:不妨设x₂ ≤ x₃ ≤ x₄ ≤ x₅,则x₂,x₃,x₄,x₅的中位数为$\frac{x₃ + x₄}{2}$,x₁,x₂,x₃,x₄,x₅,x₆的中位数为$\frac{x₃ + x₄}{2}$,故B正确;
对于选项C:
∵x₁,x₂,x₃,x₄,x₅,x₆的波动性不小于x₂,x₃,x₄,x₅的波动性,
∴x₂,x₃,x₄,x₅的标准差不大于x₁,x₂,x₃,x₄,x₅,x₆的标准差(提示:标准差反映数据的离散程度,数据越离散,标准差越大),故C错误;
对于选项D:不妨设x₂ ≤ x₃ ≤ x₄ ≤ x₅,则x₁ ≤ x₂ ≤ x₃ ≤ x₄ ≤ x₅ ≤ x₆,
∴x₅ - x₂ ≤ x₆ - x₁,即x₂,x₃,x₄,x₅的极差不大于x₁,x₂,x₃,x₄,x₅,x₆的极差(定义:极差为样本数据的最大值减去最小值),故D正确。故选BD。
[深度解析]对于选项A:
∵x₁,x₆不确定,
∴x₁,x₂,…,x₆的平均数不确定,如1,2,2,2,2,4的平均数不等于2,2,2,2的平均数,故A错误;
对于选项B:不妨设x₂ ≤ x₃ ≤ x₄ ≤ x₅,则x₂,x₃,x₄,x₅的中位数为$\frac{x₃ + x₄}{2}$,x₁,x₂,x₃,x₄,x₅,x₆的中位数为$\frac{x₃ + x₄}{2}$,故B正确;
对于选项C:
∵x₁,x₂,x₃,x₄,x₅,x₆的波动性不小于x₂,x₃,x₄,x₅的波动性,
∴x₂,x₃,x₄,x₅的标准差不大于x₁,x₂,x₃,x₄,x₅,x₆的标准差(提示:标准差反映数据的离散程度,数据越离散,标准差越大),故C错误;
对于选项D:不妨设x₂ ≤ x₃ ≤ x₄ ≤ x₅,则x₁ ≤ x₂ ≤ x₃ ≤ x₄ ≤ x₅ ≤ x₆,
∴x₅ - x₂ ≤ x₆ - x₁,即x₂,x₃,x₄,x₅的极差不大于x₁,x₂,x₃,x₄,x₅,x₆的极差(定义:极差为样本数据的最大值减去最小值),故D正确。故选BD。
10. 噪声污染问题越来越受到重视. 用声压级来度量声音的强弱, 定义声压级$L_p = 20\times\lg\frac{P}{p_0}$,其中常数$p_0(p_0>0)$是听觉下限阈值,$P$是实际声压. 下表为不同声源的声压级:

已知在距离燃油汽车、混合动力汽车、电动汽车$10m$处测得实际声压分别为$P_1,P_2,P_3$,则( )
A. $P_1\geq P_2$
B. $P_2>10P_3$
C. $P_3 = 100p_0$
D. $P_1\leq 100P_2$
答案:
10.ACD [命题点]对数的运算及实际应用
[深度解析]设燃油汽车、混合动力汽车、电动汽车的声压级分别为L,L2,L,由题知Po,P,P2,P3均大于0,
∵L−L=20×1g$\frac{P}{P}$−20xlg$\frac{P2}{Po}$=20xlg$\frac{P}{P}$≥0,
∴$\frac{P}{P2}$≥1,
∴P≥ρ2,故A正确;
∵厶−厶=20×lg$\frac{P2}{P3}$≥10,...lg$\frac{P2}{P}$≥$\frac{1}{2}$,
∴.$\frac{P2}{P}$≥ $\sqrt{10}$,
∴p2≥$\sqrt{10}$3,故B错误;
∵厶=20×1g$\frac{P3}{p}$=40,
∴$\frac{P3}{P}$=100,
∴P3=100po,故C正确;
∵L−L=20xlg$\frac{P}{P}$≤90−50=40,
∴lg$\frac{P}{P}$≤2,
∴$\frac{P}{P}$≤100,
∴P≤100p2,故D正确.
故选ACD.
一题多解
由L,=20lgPPo,对于燃油汽车60≤20lg$\frac{P}{Po}$≤90,即3≤lgP1−1gPo≤$\frac{9}{2}$,
∴lg(1000p0)=3+1gPo≤lgP≤$\frac{9}{2}$+1gPo=
lg[10po)),即10000≤p≤10茎Po;;同理,对于混合动力汽车10²;po≤p2≤1000po;对于电动汽车20lg$\frac{P}{P}$=40,则lgP3−lgPo=2,
∴lgp3=2+lgpo=lg(100po),
∴P3=100ρ0,选项C正
[深度解析]设燃油汽车、混合动力汽车、电动汽车的声压级分别为L,L2,L,由题知Po,P,P2,P3均大于0,
∵L−L=20×1g$\frac{P}{P}$−20xlg$\frac{P2}{Po}$=20xlg$\frac{P}{P}$≥0,
∴$\frac{P}{P2}$≥1,
∴P≥ρ2,故A正确;
∵厶−厶=20×lg$\frac{P2}{P3}$≥10,...lg$\frac{P2}{P}$≥$\frac{1}{2}$,
∴.$\frac{P2}{P}$≥ $\sqrt{10}$,
∴p2≥$\sqrt{10}$3,故B错误;
∵厶=20×1g$\frac{P3}{p}$=40,
∴$\frac{P3}{P}$=100,
∴P3=100po,故C正确;
∵L−L=20xlg$\frac{P}{P}$≤90−50=40,
∴lg$\frac{P}{P}$≤2,
∴$\frac{P}{P}$≤100,
∴P≤100p2,故D正确.
故选ACD.
一题多解
由L,=20lgPPo,对于燃油汽车60≤20lg$\frac{P}{Po}$≤90,即3≤lgP1−1gPo≤$\frac{9}{2}$,
∴lg(1000p0)=3+1gPo≤lgP≤$\frac{9}{2}$+1gPo=
lg[10po)),即10000≤p≤10茎Po;;同理,对于混合动力汽车10²;po≤p2≤1000po;对于电动汽车20lg$\frac{P}{P}$=40,则lgP3−lgPo=2,
∴lgp3=2+lgpo=lg(100po),
∴P3=100ρ0,选项C正
11. 已知函数$f(x)$的定义域为$R$,$f(xy)=y^{2}f(x)+x^{2}f(y)$,则( )
A. $f(0)=0$
B. $f(1)=0$
C. $f(x)$是偶函数
D. $x = 0$为$f(x)$的极小值点
答案:
11.ABC [命题点]抽象函数求值、函数的奇偶性、判断函数的极值点
[深度解析]对于A,令x=y=0,,得f
(0)=0,,故A正确;
对于B,令x=y=1,得f
(1)=∮
(1)+f
(1)=2∮
(1),所以∮
(1)=0,故B正确;
对于C,令x=y=−1,得f
(1)=f(−1)+A(−1)=2f(−1)=0,所以
A(−1)=0,所以∮(−xy)=y²f(−x)+x²f(y)=y²[∮(x)+x²f(−1)]+x²∮(y)=y²f(x)+x²f(y)=f(xy)在定义域R上恒成立,所以f(x)
是偶函数,故C正确;
对于D,函数f(x)=0为常数函数,且满足f(xy)=y²f(x)+xf(y),而常数函数没有极值点,故D错误.故选ABC.
一题多解选项D:对式子两边同时除以x²y²(x²γ²≠0),得到$\frac{xy)}{x²y²}$=
∮x(²x)+$\frac{y)}{y²}$,故可构近 $\frac{x)}{x²}$=lnlx1(x≠0),
若x=0,则由A选项知∮
(0)=0,所以f(x)={x0²,1xn=1x0l,,x≠0,
则当x>0时,f(x)=x²1nx,f'(x)=2xlnx+x².$\frac{1}{x}$=
x(2lInx+1),令f,(x)>0,则x>e²,令f'(x)<0,则0<x<e²,
故∮(x)在(0,e)上单调递减,在(e÷,+∞)上单调递增,且
1
limf(x)=limI$\frac{1}{x²}$旦x=lxi−m0−2x$\frac{1}{x²}$=

lim$\frac{x²}{−2}$=0,又f(x)是偶函数,故
f(x)的图像如图所示,所以x=0为f(x)的极大值点,故D
错误,
11.ABC [命题点]抽象函数求值、函数的奇偶性、判断函数的极值点
[深度解析]对于A,令x=y=0,,得f
(0)=0,,故A正确;
对于B,令x=y=1,得f
(1)=∮
(1)+f
(1)=2∮
(1),所以∮
(1)=0,故B正确;
对于C,令x=y=−1,得f
(1)=f(−1)+A(−1)=2f(−1)=0,所以
A(−1)=0,所以∮(−xy)=y²f(−x)+x²f(y)=y²[∮(x)+x²f(−1)]+x²∮(y)=y²f(x)+x²f(y)=f(xy)在定义域R上恒成立,所以f(x)
是偶函数,故C正确;
对于D,函数f(x)=0为常数函数,且满足f(xy)=y²f(x)+xf(y),而常数函数没有极值点,故D错误.故选ABC.
一题多解选项D:对式子两边同时除以x²y²(x²γ²≠0),得到$\frac{xy)}{x²y²}$=
∮x(²x)+$\frac{y)}{y²}$,故可构近 $\frac{x)}{x²}$=lnlx1(x≠0),
若x=0,则由A选项知∮
(0)=0,所以f(x)={x0²,1xn=1x0l,,x≠0,
则当x>0时,f(x)=x²1nx,f'(x)=2xlnx+x².$\frac{1}{x}$=
x(2lInx+1),令f,(x)>0,则x>e²,令f'(x)<0,则0<x<e²,
故∮(x)在(0,e)上单调递减,在(e÷,+∞)上单调递增,且
1
limf(x)=limI$\frac{1}{x²}$旦x=lxi−m0−2x$\frac{1}{x²}$=

lim$\frac{x²}{−2}$=0,又f(x)是偶函数,故
f(x)的图像如图所示,所以x=0为f(x)的极大值点,故D
错误,
查看更多完整答案,请扫码查看


