2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 设集合$M = \{x|0 < x < 4\}$,$N = \{x|\frac{1}{3} \leq x \leq 5\}$,则$M\cap N =$( )
A. $\{x|0 < x \leq \frac{1}{3}\}$
B. $\{x|\frac{1}{3} \leq x < 4\}$
C. $\{x|4 \leq x < 5\}$
D. $\{x|0 < x \leq 5\}$
A. $\{x|0 < x \leq \frac{1}{3}\}$
B. $\{x|\frac{1}{3} \leq x < 4\}$
C. $\{x|4 \leq x < 5\}$
D. $\{x|0 < x \leq 5\}$
答案:
B [命题点]集合的交集运算
[深度解析]
∵M={x|0<x<4},N={x|$\frac{1}{3}$≤x≤5},画出数轴如图所示.
∴M∩N={x|$\frac{1}{3}$≤x<4},故选B.

B [命题点]集合的交集运算
[深度解析]
∵M={x|0<x<4},N={x|$\frac{1}{3}$≤x≤5},画出数轴如图所示.
∴M∩N={x|$\frac{1}{3}$≤x<4},故选B.

2. 为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
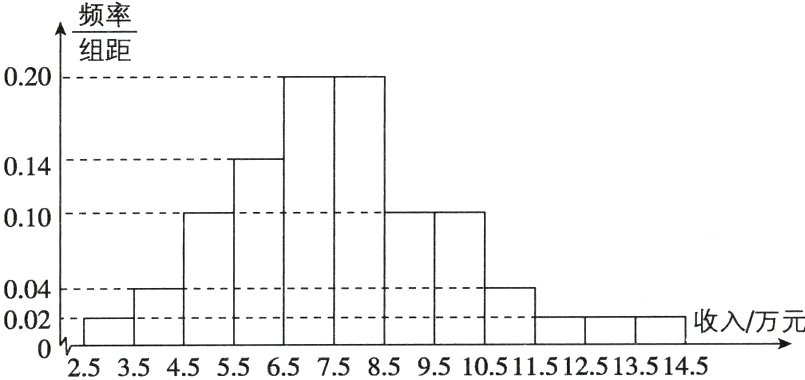
根据此频率分布直方图,下面结论中不正确的是( )
A. 该地农户家庭年收入低于$4.5$万元的农户比率估计为$6\%$
B. 该地农户家庭年收入不低于$10.5$万元的农户比率估计为$10\%$
C. 估计该地农户家庭年收入的平均值不超过$6.5$万元
D. 估计该地有一半以上的农户,其家庭年收入介于$4.5$万元至$8.5$万元之间

根据此频率分布直方图,下面结论中不正确的是( )
A. 该地农户家庭年收入低于$4.5$万元的农户比率估计为$6\%$
B. 该地农户家庭年收入不低于$10.5$万元的农户比率估计为$10\%$
C. 估计该地农户家庭年收入的平均值不超过$6.5$万元
D. 估计该地有一半以上的农户,其家庭年收入介于$4.5$万元至$8.5$万元之间
答案:
C [命题点]频率分布直方图的应用与数据分析
[深度解析]由频率分布直方图知年收入低于4.5万元的农户比率估计为(0.02 + 0.04)×1 = 0.06 = 6%,故A正确;年收入不低于10.5万元的农户比率估计为(0.04 + 0.02×3)×1 = 0.10 = 10%,故B正确;该地农户家庭年收入的平均值约为3×0.02 + 4×0.04 + 5×0.10 + 6×0.14 + 7×0.20 + 8×0.20 + 9×0.10 + 10×0.10 + 11×0.04 + 12×0.02 + 13×0.02 + 14×0.02 = 7.68>6.5,故C错误;年收入介于4.5万元至8.5万元之间的农户比率约为(0.10 + 0.14 + 0.20 + 0.20)×1 = 0.64>0.5,故D正确.故选C.
[深度解析]由频率分布直方图知年收入低于4.5万元的农户比率估计为(0.02 + 0.04)×1 = 0.06 = 6%,故A正确;年收入不低于10.5万元的农户比率估计为(0.04 + 0.02×3)×1 = 0.10 = 10%,故B正确;该地农户家庭年收入的平均值约为3×0.02 + 4×0.04 + 5×0.10 + 6×0.14 + 7×0.20 + 8×0.20 + 9×0.10 + 10×0.10 + 11×0.04 + 12×0.02 + 13×0.02 + 14×0.02 = 7.68>6.5,故C错误;年收入介于4.5万元至8.5万元之间的农户比率约为(0.10 + 0.14 + 0.20 + 0.20)×1 = 0.64>0.5,故D正确.故选C.
3.已知$(1 - i)^2z = 3 + 2i$,则$z =$ ( )
A. $-1 - \frac{3}{2}i$
B. $-1 + \frac{3}{2}i$
C. $-\frac{3}{2} + i$
D. $-\frac{3}{2} - i$
A. $-1 - \frac{3}{2}i$
B. $-1 + \frac{3}{2}i$
C. $-\frac{3}{2} + i$
D. $-\frac{3}{2} - i$
答案:
3.B [命题点]复数的四则运算
[深度解析]
∵(1 - i)²z = 3 + 2i,
∴z = $\frac{3 + 2i}{(1 - i)²}$ = $\frac{3 + 2i}{-2i}$ = $\frac{(3 + 2i)i}{-2i²}$ = $\frac{-2 + 3i}{2}$ = -1 + $\frac{3}{2}$i,故选B。
[深度解析]
∵(1 - i)²z = 3 + 2i,
∴z = $\frac{3 + 2i}{(1 - i)²}$ = $\frac{3 + 2i}{-2i}$ = $\frac{(3 + 2i)i}{-2i²}$ = $\frac{-2 + 3i}{2}$ = -1 + $\frac{3}{2}$i,故选B。
4.青少年视力是社会普遍关注的问题,视力情况可借助视力表测量,通常用五分记录法和小数记录法记录视力数据,五分记录法的数据$L$和小数记录法的数据$V$满足$L = 5 + \lg V$。已知某同学视力的五分记录法的数据为$4.9$,则其视力的小数记录法的数据约为$(\sqrt[10]{10} \approx 1.259)$ ( )
A. $1.5$
B. $1.2$
C. $0.8$
D. $0.6$
A. $1.5$
B. $1.2$
C. $0.8$
D. $0.6$
答案:
4.C [命题点]函数模型的实际应用及对数运算
[深度解析]将L = 4.9代入L = 5 + lgV,得lgV = -0.1,即V = 10⁻⁰.¹ = $\frac{1}{10^{0.1}}$ ≈ 0.8,故选C。
[深度解析]将L = 4.9代入L = 5 + lgV,得lgV = -0.1,即V = 10⁻⁰.¹ = $\frac{1}{10^{0.1}}$ ≈ 0.8,故选C。
5.已知$F_1,F_2$是双曲线$C$的两个焦点,$P$为$C$上一点,且$\angle F_1PF_2 = 60^{\circ}$,$\vert PF_1\vert = 3\vert PF_2\vert$,则$C$的离心率为
( )
A. $\frac{1}{2}$
B. $\frac{\sqrt{13}}{2}$
C. $\sqrt{7}$
D. $\sqrt{13}$
( )
A. $\frac{1}{2}$
B. $\frac{\sqrt{13}}{2}$
C. $\sqrt{7}$
D. $\sqrt{13}$
答案:
5.A [命题点]双曲线的定义及离心率,余弦定理的应用
[深度解析]不妨设双曲线的焦点在x轴上,如图,由双曲线的定义得,|PF₁| - |PF₂| = 2a,
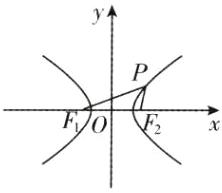
又|PF₁| = 3|PF₂|,所以|PF₂| = a,|PF₁| = 3a。所以在△F₁PF₂中,有|F₁F₂|² = |PF₁|² + |PF₂|² - 2|PF₁||PF₂|cos∠F₁PF₂,即4c² = 9a² + a² - 2×3a×a×cos60°,化简得4c² = 7a²,即$\frac{c²}{a²}$ = $\frac{7}{4}$,所以离心率e = $\frac{c}{a}$ = $\sqrt{\frac{7}{4}}$ = $\frac{\sqrt{7}}{2}$,故选A。
5.A [命题点]双曲线的定义及离心率,余弦定理的应用
[深度解析]不妨设双曲线的焦点在x轴上,如图,由双曲线的定义得,|PF₁| - |PF₂| = 2a,

又|PF₁| = 3|PF₂|,所以|PF₂| = a,|PF₁| = 3a。所以在△F₁PF₂中,有|F₁F₂|² = |PF₁|² + |PF₂|² - 2|PF₁||PF₂|cos∠F₁PF₂,即4c² = 9a² + a² - 2×3a×a×cos60°,化简得4c² = 7a²,即$\frac{c²}{a²}$ = $\frac{7}{4}$,所以离心率e = $\frac{c}{a}$ = $\sqrt{\frac{7}{4}}$ = $\frac{\sqrt{7}}{2}$,故选A。
6.在一个正方体中,过顶点$A$的三条棱的中点分别为$E,F,G$。该正方体截去三棱锥$A - EFG$后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是 ( )




答案:
6.D [命题点]几何体的三视图与直观图
[深度解析]由题意及多面体的正视图可得其直观图如图所示,则其侧视图为D选项。故选D。
[深度解析]由题意及多面体的正视图可得其直观图如图所示,则其侧视图为D选项。故选D。
7.等比数列$\{a_n\}$的公比为$q$,前$n$项和为$S_n$。设甲:$q>0$,乙:$\{S_n\}$是递增数列,则 ( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
答案:
7.B [命题点]数列的单调性及充分、必要条件的判断
[深度解析]当q = 1时,Sₙ = na₁,只有当a₁>0时,数列{Sₙ}才是递增数列,故甲不是乙的充分条件;若数列{Sₙ}是递增数列,则Sₙ - Sₙ₋₁>0对任意n≥2,n∈N*恒成立,即aₙ = a₁qⁿ⁻¹>0(n≥2,n∈N*)恒成立,所以a₁>0,q>0,因此甲是乙的必要条件。故甲是乙的必要条件但不是充分条件,故选B。
方法速记:数列{aₙ}单调性的判断方法:
(1)若aₙ - aₙ₋₁>0(n≥2,n∈N*)恒成立,则数列{aₙ}是递增数列;
(2)若aₙ - aₙ₋₁<0(n≥2,n∈N*)恒成立,则数列{aₙ}是递减数列;
(3)若aₙ - aₙ₋₁ = 0(n≥2,n∈N*)恒成立,则数列{aₙ}是常数列。
[深度解析]当q = 1时,Sₙ = na₁,只有当a₁>0时,数列{Sₙ}才是递增数列,故甲不是乙的充分条件;若数列{Sₙ}是递增数列,则Sₙ - Sₙ₋₁>0对任意n≥2,n∈N*恒成立,即aₙ = a₁qⁿ⁻¹>0(n≥2,n∈N*)恒成立,所以a₁>0,q>0,因此甲是乙的必要条件。故甲是乙的必要条件但不是充分条件,故选B。
方法速记:数列{aₙ}单调性的判断方法:
(1)若aₙ - aₙ₋₁>0(n≥2,n∈N*)恒成立,则数列{aₙ}是递增数列;
(2)若aₙ - aₙ₋₁<0(n≥2,n∈N*)恒成立,则数列{aₙ}是递减数列;
(3)若aₙ - aₙ₋₁ = 0(n≥2,n∈N*)恒成立,则数列{aₙ}是常数列。
8.2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为$8848.86$(单位:$m$),三角高程测量法是珠峰高程测量方法之一。如图是三角高程测量法的一个示意图,现有$A,B,C$三点,且$A,B,C$在同一水平面上的投影$A'$,$B'$,$C'$满足$\angle A'C'B' = 45^{\circ}$,$\angle A'B'C' = 60^{\circ}$。由$C$点测得$B$点的仰角为$15^{\circ}$,$BB'$与$CC'$的差为$100$;由$B$点测得$A$点的仰角为$45^{\circ}$,则$A,C$两点到水平面$A'B'C'$的高度差$AA' - CC'$约为$(\sqrt{3} \approx 1.732)$ ( )
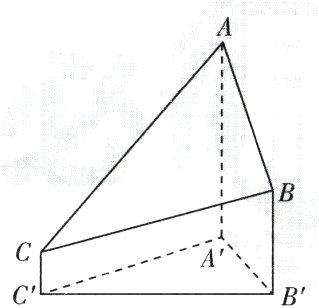
A. $346$
B. $373$
C. $446$
D. $473$

A. $346$
B. $373$
C. $446$
D. $473$
答案:
8.B [命题点]诱导公式、两角差的正弦公式以及利用正弦定理解三角形
[深度解析]如图,过点C作CD⊥BB',垂足为点D,过点D作DE⊥AA',垂足为点E,连接CE,过点B作BF⊥AA',垂足为点F,则由题意可得∠BCD = 15°,∠ABF = 45°,FE = BD = BB' - CC' = 100,AF = BF = DE,所以AA' - CC' = BF + 100。易得CD//C'B',DE//B'A',EC//A'C',所以∠ECD = ∠A'C'B' = 45°,∠EDC = ∠A'B'C' = 60°。在Rt△CDB中,CD = $\frac{100}{tan15°}$,在△CDE中,∠CED = 180° - 45° - 60° = 75°,由正弦定理,得$\frac{DE}{sin45°}$ = $\frac{CD}{sin75°}$,即DE = $\frac{100sin45°}{sin75°tan15°}$ = $\frac{100sin45°}{\frac{sin75°sin15°}{cos15°}}$ = $\frac{100sin45°}{sin15°}$。又sin15° = sin(45° - 30°) = $\frac{\sqrt{6} - \sqrt{2}}{4}$,所以DE = $\frac{100sin45°}{sin15°}$ = 100($\sqrt{3}$ + 1) ≈ 273,所以AA' - CC' = BF + 100 = DE + 100 ≈ 373,故选B。

8.B [命题点]诱导公式、两角差的正弦公式以及利用正弦定理解三角形
[深度解析]如图,过点C作CD⊥BB',垂足为点D,过点D作DE⊥AA',垂足为点E,连接CE,过点B作BF⊥AA',垂足为点F,则由题意可得∠BCD = 15°,∠ABF = 45°,FE = BD = BB' - CC' = 100,AF = BF = DE,所以AA' - CC' = BF + 100。易得CD//C'B',DE//B'A',EC//A'C',所以∠ECD = ∠A'C'B' = 45°,∠EDC = ∠A'B'C' = 60°。在Rt△CDB中,CD = $\frac{100}{tan15°}$,在△CDE中,∠CED = 180° - 45° - 60° = 75°,由正弦定理,得$\frac{DE}{sin45°}$ = $\frac{CD}{sin75°}$,即DE = $\frac{100sin45°}{sin75°tan15°}$ = $\frac{100sin45°}{\frac{sin75°sin15°}{cos15°}}$ = $\frac{100sin45°}{sin15°}$。又sin15° = sin(45° - 30°) = $\frac{\sqrt{6} - \sqrt{2}}{4}$,所以DE = $\frac{100sin45°}{sin15°}$ = 100($\sqrt{3}$ + 1) ≈ 273,所以AA' - CC' = BF + 100 = DE + 100 ≈ 373,故选B。

9.若$\alpha \in (0,\frac{\pi}{2})$,$\tan2\alpha = \frac{\cos\alpha}{2 - \sin\alpha}$,则$\tan\alpha =$ ( )
A. $\frac{\sqrt{15}}{15}$
B. $\frac{\sqrt{5}}{5}$
C. $\frac{\sqrt{5}}{3}$
D. $\frac{\sqrt{15}}{3}$
A. $\frac{\sqrt{15}}{15}$
B. $\frac{\sqrt{5}}{5}$
C. $\frac{\sqrt{5}}{3}$
D. $\frac{\sqrt{15}}{3}$
答案:
9.A [命题点]二倍角公式及同角三角函数基本关系
[深度解析]因为α∈(0,$\frac{\pi}{2}$),所以sinα>0,cosα>0。tan2α = $\frac{sin2α}{cos2α}$ = $\frac{2sinαcosα}{1 - 2sin²α}$ = $\frac{cosα}{2 - sinα}$,化简得sinα = $\frac{1}{4}$,所以cosα = $\frac{\sqrt{15}}{4}$,所以tanα = $\frac{sinα}{cosα}$ = $\frac{\sqrt{15}}{15}$,故选A。
[深度解析]因为α∈(0,$\frac{\pi}{2}$),所以sinα>0,cosα>0。tan2α = $\frac{sin2α}{cos2α}$ = $\frac{2sinαcosα}{1 - 2sin²α}$ = $\frac{cosα}{2 - sinα}$,化简得sinα = $\frac{1}{4}$,所以cosα = $\frac{\sqrt{15}}{4}$,所以tanα = $\frac{sinα}{cosα}$ = $\frac{\sqrt{15}}{15}$,故选A。
查看更多完整答案,请扫码查看


