《2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版》

13. 若$f(x) = (x - 1)^{2022} + ax + \sin(x + \frac{\pi}{2})$为偶函数，则$a = $________.

答案： 13.2　[命题点]根据函数的奇偶性求参数
[深度解析]
∵f(x) = (x - 1)² + ax + sin(x + $\frac{\pi}{2}$) = (x - 1)² + ax + cosx，
∴f(-x) = (-x - 1)² - ax + cos(-x) = (x + 1)² - ax + cosx。由于f(x)为偶函数，
∴f(x) = f(-x)，
∴(x - 1)² + ax + cosx = (x + 1)² - ax + cosx，即4x = 2ax，
∴a = 2。
快解：
∵f(x) = (x - 1)² + ax + sin(x + $\frac{\pi}{2}$) = (x - 1)² + ax + cosx为偶函数，
∴f($\frac{\pi}{2}$) = f(-$\frac{\pi}{2}$)，即($\frac{\pi}{2}$ - 1)² + a×$\frac{\pi}{2}$ + 0 = ($\frac{\pi}{2}$ + 1)² - a×$\frac{\pi}{2}$ + 0，解得a = 2。

14. 若$x,y$满足约束条件$\begin{cases}3x - 2y \leq 3\\ - 2x + 3y \leq 3\\x + y \geq 1\end{cases}$，则$z = 3x + 2y$的最大值为________.

答案：
14.15　[命题点]线性规划求最值
[深度解析]由约束条件，画出可行域如图中阴影部分所示(含边界)。
作出直线3x + 2y = 0并平移，由图可知，当直线y = -$\frac{3}{2}$x + $\frac{z}{2}$过点A时，在y轴上的截距取最大值，即目标函数z = 3x + 2y取最大值。联立$\begin{cases}-2x + 3y = 3\\3x - 2y = 3\end{cases}$，解得$\begin{cases}x = 3\\y = 3\end{cases}$，即A(3,3)，
∴目标函数的最大值zₘₐₓ = 3×3 + 2×3 = 15。

15. 在正方体$ABCD - A_1B_1C_1D_1$中，$E,F$分别为$AB,C_1D_1$的中点。以$EF$为直径的球的球面与该正方体的棱共有________个公共点

答案：
15.12　[命题点]球与正方体各棱相切问题
[深度解析]如图所示，
∵EF为球的直径，由正方体及球的对称性知，此球的球心为正方体的中心O。设正方体的棱长为2，则OF = OE = $\frac{1}{2}$EF = $\sqrt{2}$，CB = $\sqrt{2}$。
∴点O到正方体各棱的中点的距离均为$\sqrt{2}$，且正方体各面与球的交线均为圆，此圆即为正方体各面的内切圆，
∴球的球面与该正方体各棱的交点共有12个。

有　　　　个公共点

答案：

16.在△ABC中，∠BAC = 60°，AB = 2，BC = $\sqrt{6}$，∠BAC的角平分线交BC于D，则AD =　　　　。

答案：
2　[命题点]解三角形的综合应用
　　　
[深度解析]解法一:如图,在△ABC中，
　由正弦定理得$\frac{AB}{sinC}$=$\frac{BC}{sin60°}$,则sinC= $\frac{ABsin60°}{BC}$=$\frac{\sqrt{2}}{2}$,又∠BAC=60°,所以0＜C＜120°,所以C=45°.所以B=180°−C−
　∠BAC=180°−45°−60°=75°.又AD平分∠BAC,所以∠BAD=
　$\frac{1}{2}$∠BAC=30°,所以∠ADB=180°−B−∠BAD=75°=B,
　故△ABD为等腰三角形,所以AB=AD=2.
　解法二:设AD=x,AC=y,在△ABC中,由余弦定理可得BC²=
AB²+AC²−2AB.ACcos∠BAC,即y²−2y−2=0,解得y=1+　$\sqrt{3}$(舍负),又S△ABC=S△ADB+S△ADC,所以$\frac{1}{2}$×2×(1+　$\sqrt{3}$)×$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$x2x.$\frac{1}{2}$+$\frac{1}{2}$x(1+　$\sqrt{3}$)x.$\frac{1}{2}$,解得x=2.
　解法三:在△ABC中，由余弦定理得cos∠BAC=
　$\frac{AB²+AC²−BC²}{2AB.AC}$=$\frac{4+AC²−6}{4AC}$=$\frac{1}{2}$,所以AC=1+$\sqrt{3}$(舍负).在△ABD中,由正弦定理得$\frac{BD}{sinBAD}$=$\frac{AB}{sinADB}$,所以$\frac{sinADB}{sinBAD}$=
　$\frac{AB}{BD}$.在△ACD中，由正弦定理得$\frac{CD}{sinCAD}$=$\frac{AC}{sinADC}$，所以$\frac{sinADC}{sinCAD}$=$\frac{AC}{CD}$,VAD平分∠RAC所↓lsin∠RAD=sin∠CADV sin∠ADB=sin∠ADC(提示:∠ADB+∠ADC=π:所以正弦值相
等),所以$\frac{AB}{BD}$=$\frac{AC}{CD}$,所以$\frac{BD}{CD}$=$\frac{AB}{AC}$=$\frac{2}{1+\sqrt{3}}$(另解;由角平分线定理可得$\frac{BD}{CD}$=$\frac{AB}{AC}$=$\frac{2}{1+\sqrt{3}}$),且BD+CD=$\sqrt{6}$,所以BD=$\frac{2√6}{3+\sqrt{3}}$=$\sqrt{6}$−$\sqrt{2}$.在△ABC中,由余弦定理得cos∠ABC=$\frac{AB²+BC²−AC²}{2AB.BC}$=
　$\frac{4+6−(1+\sqrt{3}}{4√6}$=$\frac{\sqrt{6}\sqrt{2}}{4}$，在△ABD中，由余弦定理得cos∠ABD=$\frac{AB²+BD²−AD²}{2AB.BD}$=$\frac{2²+(\sqrt{6}\sqrt{2})²−AD}{4(√6−√2}$=$\frac{\sqrt{6}\sqrt{2}}{4}$,解得
AD=2(舍负)(点拨:本题多次运用余弦定理和正弦定理,在计算AD时,不用cos∠BAD=$\frac{AB²+AD²−BD}{2AB.AD}$建立方程的原因是分子分母都出现了AD，这样可以减少计算量{.

17.（12分）记$S_{n}$为数列$\{a_{n}\}$的前n项和，已知$a_{2}$ = 1，$2S_{n}$ = $na_{n}$。
　(1)求$\{a_{n}\}$的通项公式；
　(2)求数列$\{\frac{a_{n}+1}{2^{n}}\}$的前n项和$T_{n}$。

答案： [命题点]数列通项公式的求解、错位相减法求和
[解]
(1)2S=na。①,
　当n≥2时,2Sn−=(n−1)a−②,
　由①−②得,2an=nam−(n−1)an−1,
　即(n−1)an−1=(n−2)an.
　当n=2时,a=0;
　当n≥3时,$\frac{an−1}{n−2}$=$\frac{a}{n−1}$.
∴当n≥2时,{$\frac{a.}{n−1}$}为常数列,
∴$\frac{a}{n−1}$1　1,
∴a=n−1(n≥2).由2Sn=na,当n=1时,2a=a,a=0=1−1.
∴a=n−1(n∈N.).　　　　　　　　　　　　　　　　　5分一题多解
(1)当n=1时,2S=a,即2a=a,
∴a=0.
　　当n≥2时,由2Sm=nam,①
　　得2Sn−1=(n−1)an−1,②
　　①−②得2an=nan−(n−1)an−1,
　　整理得(n−2)am=(n−1)an−1,
　
∵a=1,
∴当n≥3时,an≠0,
∴$\frac{an}{an−1}$=$\frac{n−1}{n−2}$(n≥3),……3分当n≥3时,
　　由累乘法得$\frac{a}{an−1}$.$\frac{αn−1}{αn−2}$...$\frac{a3}{az}$=$\frac{n−1}{n−2}$.$\frac{n−2}{n−3}$..…..T2,
∴$\frac{an}{a2}$=
　　n−1.
　　又a=1,
∴an=n−1(n≥3),
　　当n=1,n=2时,a=0,a2=1满足上式,
　　故an=n−1.　　　　　　　　　　　　　　　　　　　　5分
(2)由
(1)知，$\frac{an+1}{2"}$=n−($\frac{1}{2}$
　T.=1×($\frac{1}{2}$+2×($\frac{1}{2}$)²+3×$\frac{1}{2}$3+...+n.($\frac{1}{2}$A③,
　　　　　　　　　　　　3　　　　　　　　　　　
　$\frac{1}{2}$T=1×($\frac{1}{2}$)²+2×($\frac{1}{2}$　+.….+(n−1).($\frac{1}{2}$)+n.
　　　　+1+
　($\frac{1}{2}$　④,
　　　　　　　　　　　　n
　　　　　　　　$\frac{1}{2}$[−($\frac{1}{2}$　　　　　
　由③−④得$\frac{1}{2}$T.−　　　　　　　n.$\frac{1}{2}$
　　　　　　　　　　1−$\frac{1}{2}$
　
∴T=2−(2+n).($\frac{1}{2}$.　　　　　　　　　　　　　　12分

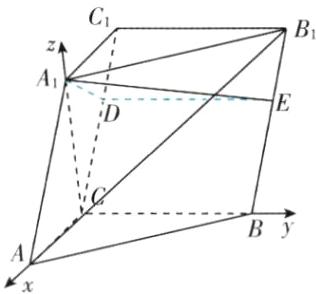
18.（12分）如图，在三棱柱$ABC - A_{1}B_{1}C_{1}$中，$A_{1}C$⊥平面ABC，∠ACB = 90°，$AA_{1}$ = 2，A到平面$BCC_{1}B_{1}$的距离为1。
　(1)证明：$AC = A_{1}C$；
　(2)已知$AA_{1}$与$BB_{1}$的距离为2，求$AB_{1}$与平面$BCC_{1}B_{1}$所成角的正弦值。
　　　　　　　　　　　　　

答案：
[命题点]线面垂直与面面垂直的判定与性质、线面角、空间向量的应用
(1)[证明]
∵AC⊥平面ABC,BC,ACC平面ABC,
∴AC⊥BC,AC⊥AC.又∠ACB=90°,
∴AC⊥BC.
∵AC∩AC=C,AC,ACC平面ACCA,
∴BC⊥平面ACCA.
∵BCC平面BCCB,
∴平面ACCA⊥平面BCCB.……2分如图，过点A作AD⊥CC，于点D,
∵平面ACCA⊥平面BCCB,平面ACCA∩平面BCCB=
CC,ADC平面ACCA,
∴AD⊥平面BCCB,
∴AD=1.
∵AC、//AC,
∴AC⊥AC
　由棱柱的性质知CC=AA=2,
∴S△ACC=$\frac{1}{2}$!C.AC=$\frac{1}{2}$CC.AD=1①.
　又A,C²+AC²=CC²=4②,
　联立①②,解得AC=AC=$\sqrt{2}$　　　　　　　　　　　　5分由棱柱的性质知A,C=AC,
∴AC=AC=$\sqrt{2}$　　　　　　　6分
(2)[解]如图,过点D作DE//BC
　交BB，于点E,连接AE,则DE⊥
　平面ACCA.
∵CCC平面ACCA,
∴DE⊥CC..
　　　　　　　　　　　　　　　
∵DE∩AD=D,DE,ADC平面
ADE,
∴CC⊥平面ADE.
∵AEC平面ADE,
∴CC⊥AE.
　由棱柱的性质知,AA//CC、//BB,
∴AA⊥AEBB⊥AE,　　　　　　　　　　　　　　　8分
∴线段AE的长即为AA，与BB，的距离，
∴AE=2,
∴DE=$\sqrt{AE²−AD²}$=$\sqrt{3}$
　易知四边形DEBC为平行四边形，
∴BC=DE=$\sqrt{3}$
　由
(1)知直线CA,CA,CB两两垂直，故以点C为坐标原点，建立如图所示的空间直角坐标系，则C(0,0,0),A(√2,0,0)，
B(0,√3,0),B,(−$\sqrt{2}$,√3,√2),
∴AB=(−2√2,$\sqrt{3}$,√2),CB=
　(|　$\sqrt{2}$$\sqrt{3}$,√2),CB=(0,√3,0).　　　　　　　　　　　　10分设平面BCC,B,的法向量为n=(x,y,z)，
　则{nn..CCBB==00,,即{√3y$\sqrt{2}$=x0,$\sqrt{3}$y+$\sqrt{2}$z=0,
　令x=1,则y=0,z=1,
∴n=(1,0,1).
　设直线AB，与平面BCC,B，所成角为θ,
　　　　　　　　　　　　司
　则sinθ=|cos＜AB,n＞｜=$\frac{AB.n}{AB11n|}$$\frac{\sqrt{2}}{\sqrt{8+3+2}\sqrt{2}}$=$\frac{\sqrt{13}}{13}$.
　　　　　　　　　　　　　　　　　　　　　　12分一题多解
(2)如图,连接AB,
　
∵AC=AC,BC⊥A,C,BC⊥AC,
　
∴△ABC△ABC,
　
∴AB=AB.　　　　　　　　8分
　　　　　　　　　　　　　　　 过B作BD⊥AA交AA于D,则D
　　为AA的中点.
　
∵AA与BB的距离为2,
∴BD=2.
　　过点A作AE⊥BB,交BB的延长
　　线于E,
　　则AE=2,BE=AD=1,B1E=3,
　　在Rt△AEB中,AB=$\sqrt{AE²+BE²}$=　$\sqrt{2²+3²}$=$\sqrt{13}$……10分又A到平面BCCB的距离为1,
　　则AB，与平面BCCB所成角的正弦值$\frac{1}{\sqrt{13}}$=$\frac{\sqrt{13}}{13}$　...12分