《2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版》

11. 已知a＞0, b＞0, 且a + b = 1, 则 (　　)
　　
A. a² + b² ≥ $\frac{1}{2}$　　　　　　B. 2^(a - b) ＞ $\frac{1}{2}$
　　
C. log₂a + log₂b ≥ - 2　　　　D. $\sqrt{a}$ + $\sqrt{b}$ ≤ $\sqrt{2}$

答案： 11.ABD　[命题点]基本不等式的应用
[深度解析]由$a\gt0$，$b\gt0$，$a + b = 1$，得$\frac{a^2 + b^2}{2} \geq (\frac{a + b}{2})^2 = \frac{1}{4}$，即$a^2 + b^2 \geq \frac{1}{2}$，当且仅当$a = b = \frac{1}{2}$时取等号，故A正确；
由$a\gt0$，$b\gt0$，$a + b = 1$，得$a - b = 2a - 1\gt -1$，故$2^{a - b}\gt\frac{1}{2}$，故B正确；
$\lg a + \lg b = \lg(ab) \leq \lg(\frac{a + b}{2})^2 = \lg(\frac{1}{2})^2 = -2$，当且仅当$a = b = \frac{1}{2}$时，等号成立，故C错误（另解：令$a = \frac{1}{4}$，$b = \frac{3}{4}$，则$\lg a + \lg b\lt -2$，故C错误）；
$(\sqrt{a} + \sqrt{b})^2 = a + b + 2\sqrt{ab} = 1 + 2\sqrt{ab} \leq 1 + a + b = 2$，得$\sqrt{a} + \sqrt{b} \leq \sqrt{2}$，当且仅当$a = b = \frac{1}{2}$时，等号成立，故D正确。故选ABD。
方法速记：灵活利用基本不等式的变形，掌握$ab\leq(\frac{a + b}{2})^2\leq\frac{a^2 + b^2}{2}$。

12. 信息熵是信息论中的一个重要概念. 设随机变量X所有可能的取值为1, 2, …, n, 且P(X = i) = pᵢ＞0 (i = 1, 2, …, n), $\sum_{i = 1}^{n}p_{i}$ = 1, 定义X的信息熵H(X) = - $\sum_{i = 1}^{n}p_{i}\log_{2}p_{i}$ (　　)
　
A. 若n = 1, 则H(X) = 0
　
B. 若n = 2, 则H(X)随着p₁的增大而增大
　
C. 若pᵢ = $\frac{1}{n}$ (i = 1, 2, …, n), 则H(X)随着n的增大而增大
　
D. 若n = 2m, 随机变量Y所有可能的取值为1, 2, …, m, 且P(Y = j) = pⱼ + p₂ₘ₊₁₋ⱼ (j = 1, 2, …, m), 则H(X) ≤ H(Y)

答案： 12.AC　[命题点]概率统计的新定义问题
[深度解析]$H(X) = -p\log_2 p$，当$n = 1$时，$p = 1$，$H(X) = -p\log_2 p = 0$，故A正确。
当$n = 2$时，$0\lt p_1\lt1$，$\log_2 p_1\lt0$，$p_1 + p_2 = 1$，则$H(X) = -[p_1\log_2 p_1 + (1 - p_1)\log_2(1 - p_1)]$。
解法一：令$f(p) = -p\log_2 p - (1 - p)\log_2(1 - p)$，由$f(p) = f(1 - p)$知$f(p)$的图像关于直线$p = \frac{1}{2}$对称，则在$(0,1)$上总能找到两个不同的值，使得对应的$H(X)$相等，故B错误。
解法二：设$f(p) = -[p\log_2 p + (1 - p)\log_2(1 - p)]$，则$f^\prime(p) = -[\log_2 p + p\cdot\frac{1}{p\ln2} - \log_2(1 - p) + (1 - p)\cdot\frac{-1}{(1 - p)\ln2}] = \log_2\frac{1 - p}{p}$，当$0\lt p\lt\frac{1}{2}$时，$f^\prime(p)\gt0$；当$p\gt\frac{1}{2}$时，$f^\prime(p)\lt0$，故B错误。
当$p = \frac{1}{n}$时，$H(X) = \frac{1}{n}\sum_{i = 1}^{n}\log_2\frac{1}{n} = \frac{1}{n}\times n\times\log_2\frac{1}{n} = \log_2 n$，则$H(X)$随$n$的增大而增大，故C正确。
当$n = 2m$时，$Y = 1,2,\cdots,m$，$P(Y = j) = p_j + p_{2m + 1 - j}$（$j = 1,2,\cdots,m$），$p_i\gt0$，则$H(X) = -(p_1\log_2 p_1 + p_2\log_2 p_2 + \cdots + p_{2m}\log_2 p_{2m})$，$H(Y) = -[(p_1 + p_{2m})\log_2(p_1 + p_{2m}) + (p_2 + p_{2m - 1})\log_2(p_2 + p_{2m - 1}) + \cdots + (p_m + p_{m + 1})\log_2(p_m + p_{m + 1})] = -[p_1\log_2(p_1 + p_{2m}) + p_2\log_2(p_2 + p_{2m - 1}) + \cdots + p_{2m}\log_2(p_{2m} + p_1)]$，则$H(X) - H(Y) = p_1\log_2\frac{p_1 + p_{2m}}{p_1} + p_2\log_2\frac{p_2 + p_{2m - 1}}{p_2} + \cdots + p_{2m}\log_2\frac{p_{2m} + p_1}{p_{2m}} = p_1\log_2(1 + \frac{p_{2m}}{p_1}) + p_2\log_2(1 + \frac{p_{2m - 1}}{p_2}) + \cdots + p_{2m}\log_2(1 + \frac{p_1}{p_{2m}})\gt0$，所以$H(X)\gt H(Y)$，故D错误。故选AC。
方法速记：将新定义的关系式转化为函数式研究，当$n = 1$时，直接求值；当$n = 2m$时，作差比较$H(X)$与$H(Y)$。

13. 斜率为 $\sqrt{3}$ 的直线过抛物线C: y² = 4x的焦点, 且与C交于A, B两点, 则|AB| = ________.

答案： 13.$\frac{16}{3}$　[命题点]直线与抛物线的位置关系及弦长
[深度解析]由$y^2 = 4x$，得其焦点$F(1,0)$。又直线$AB$的斜率为$\sqrt{3}$，所以直线$AB$的方程为$y = \sqrt{3}(x - 1)$。联立$\begin{cases}y = \sqrt{3}(x - 1)\\y^2 = 4x\end{cases}$，得$3x^2 - 10x + 3 = 0$，设$A(x_A,y_A)$，$B(x_B,y_B)$，则$x_A + x_B = \frac{10}{3}$。又$|AF| = x_A + 1$，$|BF| = x_B + 1$（提示：利用抛物线定义表示$|AF|$，$|BF|$），所以$|AB| = |AF| + |BF| = x_A + x_B + 2 = \frac{10}{3} + 2 = \frac{16}{3}$。
方法速记：过抛物线$y^2 = 2px(p\gt0)$焦点的直线与抛物线交于$A(x_A,y_A)$，$B(x_B,y_B)$两点，则$|AB| = x_A + x_B + p$。
快解：设斜率为$\sqrt{3}$的直线倾斜角为$\theta$，则$\theta = \frac{\pi}{3}$，所以$|AB| = \frac{2p}{\sin^2\theta} = \frac{4}{\sin^2\frac{\pi}{3}} = \frac{16}{3}$（提示：过抛物线$y^2 = 2px(p\gt0)$焦点且倾斜角为$\theta$的直线与抛物线相交所得弦长公式）。

14. 将数列{2n - 1}与{3n - 2}的公共项从小到大排列得到数列{aₙ}, 则{aₙ}的前n项和为________.

答案： 14.3n^2 - 2n　[命题点]等差数列求和
[深度解析]数列$\{2n - 1\}$表示首项为$1$，公差为$2$的等差数列，各项均为正奇数，而数列$\{3n - 2\}$表示首项为$1$，公差为$3$的等差数列，各项分别为交替出现的正奇数与正偶数，它们的公共项为数列$\{3n - 2\}$中的奇数项，所以$\{a_n\}$是首项为$1$，公差为$6$的等差数列，其前$n$项和$S_n = n\times1 + \frac{n(n - 1)}{2}\times6 = 3n^2 - 2n$。
易错警示：注意公共项组成的新数列公差的改变。

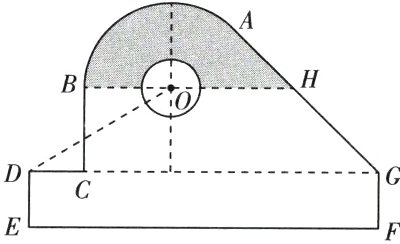
15. 某中学开展劳动实习, 学生加工制作零件, 零件 截面如图所示. O为圆孔及轮廓圆弧AB所在圆的圆心, A是圆弧AB与直线AG的切点，B是圆弧AB与直线BC的切点, 四边形DEFG为矩形, BC⊥DG, 垂足为C, tan∠ODC = $\frac{3}{5}$, BH//DG, EF = 12cm,
DE = 2cm, A到直线DE和EF的距离均为7cm, 圆孔半径为1cm, 则图中阴影部分的面积为________cm².

答案：
15.$\frac{5\pi}{2} + 4$　[命题点]三角形与扇形面积的应用
[深度解析]连接$OA$，过点$A$作$EF$的垂线，分别交$BH$，$DG$于点$M$，$N$，过点$O$作垂直于$CG$的直线与$CG$交于点$P$，则由$EF = 12$，$DE = 2$，$A$到直线$DE$和$EF$的距离为$7$可知$AN = NG = 5$，则$\angle MAH = \frac{\pi}{4}$。又$OA\perp AG$，所以$\triangle AOM$为等腰直角三角形，$\angle AOM = \frac{\pi}{4}$，$\angle AOB = \frac{3\pi}{4}$。令$AM = OM = MH = PN = x$，则$OP = MN = 5 - x$，$DP = 7 - x$，$OA = AH = \sqrt{2}x$，由$\tan\angle ODC = \frac{OP}{DP} = \frac{5 - x}{7 - x} = \frac{3}{5}$，得$x = 2$，则$OA = 2\sqrt{2}$，所以$S_{\triangle OAH} = \frac{1}{2}\cdot OA\cdot AH = 4$，$S_{扇形OAB} = \frac{1}{2}\times\frac{3\pi}{4}\times OA^2 = \frac{3\pi}{8}\times8 = 3\pi$，圆孔半径为$1$，则$S_{半圆O} = \frac{1}{2}\pi\times1^2 = \frac{\pi}{2}$，所以$S_{阴影} = S_{扇形OAB} + S_{\triangle OAH} - S_{半圆O} = 3\pi + 4 - \frac{\pi}{2} = \frac{5\pi}{2} + 4$。

16.已知直四棱柱ABCD−A₁B₁C₁D₁的棱长均为2,∠BAD = 60°.以D为球心,$\sqrt{5}$为半径的球面与侧面BCC₁B₁的交线长为________.

答案：
[命题点]直四棱柱的侧面被球截得的弧长
[深度解析]如图，直四棱柱ABCD - A₁B₁C₁D₁的棱长都为2，∠BAD = 60°，则△ABD与△B₁C₁D₁均为边长为2的等边三角形。
　　　　　　　　　　　　　　
在侧面BCC₁B₁内要找到与点D连线的长度为√5的点的轨迹，取BC的中点为E，连接DE，得DE⊥BC，又BB₁⊥DE，BC∩BB₁ = B，所以DE⊥平面BCC₁B₁，DE = √3。取BB₁、CC₁的中点分别为F、G，连接EF、EG，则EF = EG = √2，DF = DG = √5，于是以D为球心，√5为半径的球与侧面BCC₁B₁的交线为圆弧FG，其中弧FG所在圆的圆心为E，半径EF = √2，∠FEG = 90°，则所求的交线长即圆弧FG的长等于π/2 × √2 = √2π/2。

17. (本小题满分10分)在①ac = $\sqrt{3}$，②csinA = 3，③c = $\sqrt{3}$b这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求c的值；若问题中的三角形不存在，说明理由。
问题: 是否存在△ABC，它的内角A，B，C的对边分别为a，b，c，且sinA = $\sqrt{3}$sinB，C = $\frac{\pi}{6}$，________?
注: 如果选择多个条件分别解答，按第一个解答计分。

答案： [命题点]利用正弦定理、余弦定理解三角形
[解]方案一:选条件①
由C = $\frac{\pi}{6}$和余弦定理得$\frac{a^{2}+b^{2}-c^{2}}{2ab}$ = $\frac{\sqrt{3}}{2}$。3分
由sinA = $\sqrt{3}$sinB及正弦定理得a = $\sqrt{3}$b。5分
于是$\frac{(\sqrt{3}b)^{2}+b^{2}-c^{2}}{2\times\sqrt{3}b\times b}$ = $\frac{\sqrt{3}}{2}$，由此可得b = c。8分
由①ac = $\sqrt{3}$，解得a = $\sqrt{3}$，b = c = 1。9分
因此，选条件①时问题中的三角形存在，此时c = 1。10分
方案二:选条件②
由C = $\frac{\pi}{6}$和余弦定理得$\frac{a^{2}+b^{2}-c^{2}}{2ab}$ = $\frac{\sqrt{3}}{2}$。3分
由sinA = $\sqrt{3}$sinB及正弦定理得a = $\sqrt{3}$b。5分
于是$\frac{(\sqrt{3}b)^{2}+b^{2}-c^{2}}{2\times\sqrt{3}b\times b}$ = $\frac{\sqrt{3}}{2}$，由此可得b = c，B = C = $\frac{\pi}{6}$，A = $\frac{2\pi}{3}$。
由②csinA = 3，所以c = b = 2$\sqrt{3}$，a = 6。8分
因此，选条件②时问题中的三角形存在，此时c = 2$\sqrt{3}$。10分
方案三:选条件③
由C = $\frac{\pi}{6}$和余弦定理得$\frac{a^{2}+b^{2}-c^{2}}{2ab}$ = $\frac{\sqrt{3}}{2}$。3分
由sinA = $\sqrt{3}$sinB及正弦定理得a = $\sqrt{3}$b。5分
于是$\frac{(\sqrt{3}b)^{2}+b^{2}-c^{2}}{2\times\sqrt{3}b\times b}$ = $\frac{\sqrt{3}}{2}$，由此可得b = c。8分
由③c = $\sqrt{3}$b，与b = c矛盾。9分
因此，选条件③时问题中的三角形不存在。10分