《2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版》

1. 已知集合$A = \{ - 1,1,2,4\}$，$B = \{ x|\vert x - 1\vert\leq1\}$，则$A\cap B =$( )
A. $\{ - 1,2\}$
B. $\{ 1,2\}$
C. $\{ 1,4\}$
D. $\{ - 1,4\}$

答案： B [命题点]集合的基本运算
[深度解析]由|x - 1| ≤ 1，得 - 1 ≤ x - 1 ≤ 1，解得 0 ≤ x ≤ 2，所以 B = {x|0 ≤ x ≤ 2}，所以 A ∩ B = {1, 2}，故选 B。
快解：因为 4 ∉ B，所以 4 ∉ A ∩ B，故排除 C、D；因为 - 1 ∉ B，所以 - 1 ∉ A ∩ B，故排除 A。故选 B。

2. $(2 + 2i)(1 - 2i)=$( )
A. $- 2 + 4i$
B. $- 2 - 4i$
C. $6 + 2i$
D. $6 - 2i$

答案： D [命题点]复数的乘法运算
[深度解析](2 + 2i)(1 - 2i) = 2 - 4i + 2i + 4 = 6 - 2i，故选 D。

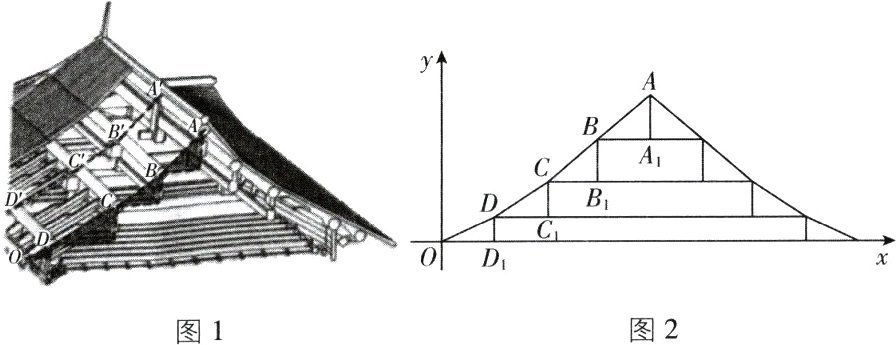
3. 图1是中国古代建筑中的举架结构，$AA'$，$BB'$，$CC'$，$DD'$是桁，相邻桁的水平距离称为步，垂直距离称为举。图2是某古代建筑屋顶截面的示意图，其中$DD_1$，$CC_1$，$BB_1$，$AA_1$是举，$OD_1$，$DC_1$，$CB_1$，$BA$是相等的步，相邻桁的举步之比分别为$\frac{DD_1}{OD_1}=0.5$，$\frac{CC_1}{DC_1}=k_1$，$\frac{BB_1}{CB_1}=k_2$，$\frac{AA_1}{BA}=k_3$。已知$k_1$，$k_2$，$k_3$成公差为$0.1$的等差数列，且直线$OA$的斜率为$0.725$，则$k_3=$( )

A. $0.75$
B. $0.8$
C. $0.85$
D. $0.9$

答案：
D [命题点]等差数列的性质、斜率与倾斜角在数学文化中的应用
[深度解析]如图，连接 OA，延长 AA₂与 x 轴交于点 A₂，则 OA₂ = 4OD。因为 k₁，k₂，k₃成公差为 0.1 的等差数列，所以 k₁ = k₃ - 0.2，k₂ = k₃ - 0.1。
因为 CC₁ = DC₁(k₃ - 0.2)，BB₁ = CB(k₃ - 0.1)，AA₂ = k₃BA，即 CC₁ = OD(k₃ - 0.2)，BB₁ = OD(k₃ - 0.1)（利用直线和 OD 表示出来）。又$\frac{DD₁}{OD}$ = 0.5，所以 DD₁ = 0.5OD，所以 AA₂ = 0.5OD + OD(k₃ - 0.2) + OD(k₃ - 0.1) + k₃OD = OD(3k₃ - 0.2)。所以 tan∠A₂OA = $\frac{AA₂}{OA₂}$ = $\frac{OD(3k₃ - 0.2)}{4OD}$ = 0.725，解得 k₃ = 0.9，故选 D。
快解：如图，连接 OA，延长 AA₂与 x 轴交于点 A₂。设 OD = DC₁ = CB = BA = 1，则 CC₁ = k₁，BB₁ = k₂，AA₂ = k₃。因为 k₁，k₂，k₃成公差为 0.1 的等差数列，所以 CC₁ = k₁ = k₃ - 0.2，BB₁ = k₂ = k₃ - 0.1。又$\frac{DD₁}{OD}$ = 0.5，所以 DD₁ = 0.5，所以 tan∠A₂OA = $\frac{AA₂}{OA₂}$ = $\frac{DD₁ + CC₁ + BB₁ + AA₂}{OD + DC₁ + CB + BA}$ = 0.725，解得 k₃ = 0.9，故选 D。

4. 已知向量$\vec{a}=(3,4)$，$\vec{b}=(1,0)$，$\vec{c}=\vec{a}+t\vec{b}$，若$\langle\vec{a},\vec{c}\rangle=\langle\vec{b},\vec{c}\rangle$，则$t=$( )
A. $- 6$
B. $- 5$
C. $5$
D. $6$

答案： C [命题点]平面向量运算的坐标表示、平面向量的夹角
[深度解析]由题意，得 c = a + tb = (3 + t, 4)，所以 a·c = 25 + 3t，b·c = 3 + t。因为〈a, c〉 = 〈b, c〉，所以 cos〈a, c〉 = cos〈b, c〉，所以$\frac{a·c}{|a||c|}$ = $\frac{b·c}{|b||c|}$，所以$\frac{a·c}{|a|}$ = $\frac{b·c}{|b|}$，即$\frac{25 + 3t}{5}$ = $\frac{3 + t}{1}$，解得 t = 5，故选 C。
快解：设$\overrightarrow{OA}$ = a，$\overrightarrow{OB}$ = b，$\overrightarrow{OC}$ = c，由〈a, c〉 = 〈b, c〉，得点 C 在∠AOB 平分线所在的直线上。$\frac{a}{|a|}$ + $\frac{b}{|b|}$与 c 共线，即 c = λ($\frac{a}{|a|}$ + $\frac{b}{|b|}$)（λ 为常数），又 c = a + tb，所以 t = $\frac{|a|}{|b|}$ = 5。故选 C。

5. 甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演，若甲不站在两端，丙和丁相邻，则不同的排列方式共有(　　　)
A.12种　　
　B.24种　　
　C.36种　　
　D.48种

答案： 5.B　[命题点]排列组合、$\frac{1}{分}$分步乘法计数原理
[深度解析]先将丙和丁捆在一起有A2种排列方式(提示:对于元素相邻的排列问题选用“捆绑法”)，然后将其与乙、戊排列有
A3种排列方式,取后将中插入中间两空中的一个，有C{种排列方式,则由分步乘法计数原理得不同的排列方式共有A2AC=
　24(种),故选B.

6. 若$\sin(\alpha +\beta) + \cos(\alpha +\beta) = 2\sqrt{2}\cos(\alpha + \frac{\pi}{4})\sin\beta$，则(　　　)
A.$\tan(\alpha - \beta) = 1$　　　　　
　B.$\tan(\alpha + \beta) = 1$
C.$\tan(\alpha - \beta) = -1$　　　　
　D.$\tan(\alpha + \beta) = -1$

答案： 6.C　[命题点]两角和与差的正弦、余弦公式，同角三角函数的基本关系
[深度解析]由已知等式,得sinαxcosβ+sinβcosα+cosαcosβ−sinαsinβ=2√2×$\frac{\sqrt{2}}{2}$(cosα−sinα)sinβ,整理得sinαcosβ−sinβcosα+cosαcosβ+sinαsinβ=0,即sin(α−β)+cos(α−β)=0,所以tan(α−β)=−1,故选C.
　一题多解(特殊值法)令β=0,则由已知等式,得sinα+cosα=0,取α=
　$\frac{3π}{4}$,得tan(α−β)=tan(α+β)=−1,故排除A,B;令α=0,则由已知等式,得sinβ+cosβ=2sinβ,即sinβ=cosβ,,取β=$\frac{H}{4}$,则tan(α−β)=−1,tan(α+B)=1,故排除D.故选C.

7. 已知正三棱台的高为1，上、下底面边长分别为$3\sqrt{3}$和$4\sqrt{3}$，其顶点都在同一球面上，则该球的表面积为(　　　)
A.100π　　
　B.128π　　
　C.144π　　
　D.192π

答案： 7.A[命题点]正棱台外接球的表面积
[深度解析]由题意，得正三棱台上、下底面的外接圆的半径分别为$\frac{2}{3}$x$\frac{\sqrt{3}}{2}$x3√3=3,$\frac{2}{3}$x$\frac{\sqrt{3}}{2}$x4$\sqrt{3}$=4.设该正三棱台上、下底面的外接圆的圆心分别为01,02,外接球的半径为R,球心为0,则0,02=1,球心0在直线0,02上.由于球心位置不能确定，需分球心在线段002上和不在线段002上两种情况讨论.当球心在线段002上时,R²=3²+00²=4²+(1−00,)²,解得00=4＞1,不符合题意;当球心不在线段002上,即球心在线段002的延长线上时,R²=4²+00²=3²+(1+002)²,解得002=3,所以R²=25.综上,球0的表面积为4πR²=100π,故选A.

8. 已知函数$f(x)$的定义域为$R$，且$f(x + y) + f(x - y) = 2f(x)f(y)$，$f(1) = 1$，则$\sum_{k = 1}^{2024}f(k)=$(　　　)
A.−3　　　
　B.−2　　　
　C.0　　　　
　D.1

答案： 8.A
[命题点]抽象函数的周期性
[深度解析]在f(x+y)+f(x−y)=∮(x).f(y)中,含y=1,得∮(x+1)+f(x−1)=f(x)
(1),所以f(x+1)+f(x−1)=f(x)①,,所以∮(x+2)+f(x)=f(x+1)②.由①②相加,整理得∮(x+2)+∮(x−1)=0,所以∮(x+3)+f(x)=0,即∮(x+3)=−f(x),所以f(x+6)=−∮(x+3)=∮(x),所以函数∮(x)的一个周期为6.在f(x+y)+f(x−y)=∮(x)∮(y)中,令y=0,得∮(x)+f(x)=∮(x)∮
(0),所以∮
(0)=
　2.令x=1,y=1,得f
(2)+∮
(0)=∮
(1)f
(1),所以f
(2)=−1.由f(x+3)=
−f(x),得f
(3)=−∮
(0)=−2、f
(4)=|∮
(1)=−1∮
(5)=−A
(2)=1f
(6)=
　−2f2
(3)=2,所以f
(1)+f
(2)+.….+∮
(6)=1−1−2−1+1+2=0.所以∑∮(k)=3[f
(1)+A
(2)+.….+A
(6)]+f
(1)+A
(2)+f
(3)+f
(4)=
　3×0+1−1−2−1=−3,故选A.

9. 已知函数$f(x) = \sin(2x + \varphi)(0 \lt \varphi \lt \pi)$的图像关于点$(\frac{2\pi}{3},0)$中心对称，则(　　　)
A.$f(x)$在区间$(0,\frac{5\pi}{12})$单调递减
B.$f(x)$在区间$(-\frac{\pi}{12},\frac{11\pi}{12})$有两个极值点
C.直线$x = \frac{7\pi}{6}$是曲线$y = f(x)$的对称轴
D.直线$y = \frac{\sqrt{3}}{2} - x$是曲线$y = f(x)$的切线

答案： 9.AD　[命题点]正弦型三角函数的图像与性质
[深度解析]因为函数∮(x)的图像关于点($\frac{2π}{3}$,0)中心对称,所以si{(2×$\frac{2π}{3}$+)=0,则$\frac{4π}{3}$+=kπ(k∈Z),结合0＜6＜π,得=$\frac{2π}{3}$,所以f(x)=sin(2x+$\frac{2π}{3}$
　对于A,由2kπ+$\frac{T}{2}$≤2x+$\frac{2π}{3}$≤2kπ+$\frac{3π}{2}$(k∈Z),得kTπ−$\frac{T}{12}$≤x≤kπ+$\frac{5π}{12}$(k∈Z),当k=0时,−$\frac{T}{12}$≤x≤$\frac{5}{12}$.因为(0,$\frac{5π}{12}${⊆
[−$\frac{T}{12}$,$\frac{5π}{12}$,所以函数(x))在区间(0,$\frac{5π}{12}$单调递减，故A正确.对于B,由2x+23=kπ+$\frac{H}{2}$(k∈Z),得x=$\frac{kT}{2}$−$\frac{T}{12}$(k∈Z),当k=0 时,x=$\frac{T}{12}$;当k=1时,x=$\frac{5π}{12}$;当k=2时，x=$\frac{11π}{12}$,所以函数f(x)在区间($\frac{T}{12}$,$\frac{11}{12}$只有一个极值点，故B不正确.
　对于C,由选项B的分析知,函数∮(x)图像的对称轴方程为x=
　$\frac{kTT}{2}$−$\frac{1}{12}$(k∈Z),而方程$\frac{kTπ}{2}$$\frac{T}{12}$=$\frac{7π}{6}$(k∈Z)无解，故C不正确.
　(另解:因为八$\frac{7π}{6}$)=sin(2×$\frac{7π}{6}$))=sin3π=0,所以直线x=
　$\frac{7π}{6}$不是曲线y=/(x)的对称轴,故C不正确)
　对于DJα(x)=2cos(2x+$\frac{2π}{3}${,若直线y=$\frac{\sqrt{3}}{2}$x为曲线y=f(x)的切线,则由2cos(2x+$\frac{2π}{3}$=−1得2x+$\frac{2π}{3}$=2kπ+$\frac{2π}{3}$(k∈Z)或2x+$\frac{2π}{3}$=2kπ+3(k∈Z),所以x=kπ((k∈Z)或x=kπ+$\frac{H}{3}$(keZ).当x=kπ(k∈Z)时f(x)=$\frac{\sqrt{3}}{2}$,则由$\frac{√3}{2}$=$\frac{\sqrt{3}}{2}$−kπ(k∈Z),解得k=
　0;当x=kπ+$\frac{H}{3}$(k∈Z)时,∮(x)=−$\frac{\sqrt{3}}{2}$,方程−$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$−kπ−$\frac{H}{3}$(keZ)无解.综上所述,直线y=$\frac{\sqrt{3}}{2}$−x为曲线y=f(x)的切线,故
D正确.故选AD.

10. 已知$O$为坐标原点，过抛物线$C:y² = 2px(p \gt 0)$焦点$F$的直线与$C$交于$A,B$两点，其中$A$在第一象限，点$M(p,0)$。若$\vert AF\vert = \vert AM\vert$，则(　　　)
A.直线$AB$的斜率为$2\sqrt{6}$
B.$\vert OB\vert = \vert OF\vert$
C.$\vert AB\vert \gt 4\vert OF\vert$
D.$\angle OAM + \angle OBM \lt 180^{\circ}$

答案： 10.ACD　[命题点]抛物线的性质、余弦定理、直线与抛物线的位置关系
[深度解析]对于A,因为IAFI=IAMI,且M(p,0)，F($\frac{p}{2}$”所以xA=$\frac{xp+xM}{2}$=43p,代入抛物线方程y²=2px(p＞0),解得y=
　　　　　　　　　　　　　　　$\frac{\sqrt{6}}{2}$−
　　p,所以A(,$\frac{\sqrt{6}}{2}$ρ),所以ka=kax=$\frac{2}{3P}$=2√6,故A
　　　　　　　　　　　　　　　$\frac{3}{4}$$\frac{P}{2}$
　正确;
　对于B,由选项A的分析,,知直线AB的方程为y=2$\sqrt{6}$(x−$\frac{P}{2}$),代人γ²=2px,,得12x²−13pxx+3p²=0,,解得x=$\frac{3}{4}$或x=
　p,所以xB=$\frac{1}{3}$p,所以y=−$\frac{\sqrt{6}}{3}$p,所以1OB|=　$\sqrt{x2+y²}$=
$\sqrt{7}$≠$\frac{P}{2}$=IOFI,故B不正确;
　对于C,由抛物线的定义及选项B的分析,得1ABI=xA+xB+p=
　$\frac{25}{12}$＞2p(提示:关于直线AB被抛物线y²=2px(p＞0)截得的弦长问题要注普吉线是不过抽物线的准占艾过物线的难店可直接使用公式IABI=xA+xB+p),即IABI＞4IOFI,故C正确;对于D,因为10A1=$\frac{\sqrt{33}}{4}$p,IAM|=$\frac{5}{4}$p,1OB|=$\frac{\sqrt{7}}{3}$p,IBMI=
　$\frac{\sqrt{10}}{3}$P,所以由余弦定理，　得　cos　∠OAM=
　$\frac{IOA1²+1AM1²−1OM1}{210A|.IAM|}$=$\frac{33}{16}$²++126P²−p²=$\frac{21}{5\sqrt{33}}$＞0,cos∠OBM=
　　　　　　　　　2×$\frac{\sqrt{33}}{4}$x$\frac{5}{4}$
　$\frac{1OB1²+1BM1²−1OM1}{21OB|.IBMI}$=$\frac{7}{9}$$\sqrt{7}$²++10P²−p²=$\frac{4}{\sqrt{70}}$＞0,所以∠0Ay＜2×px$\frac{\sqrt{10}}{3}$
　90°∠OBM＜90°(易错:注意角的取值范围),所以∠0AM+∠OBM＜180°，故D正确.故选ACD.

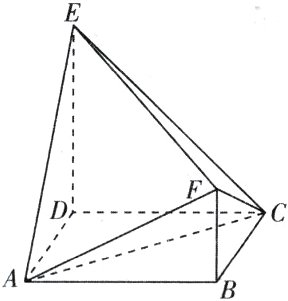
11. 如图，四边形$ABCD$为正方形，$ED \perp$平面$ABCD$，$FB // ED$，$AB = ED = 2FB$。记三棱锥$E - ACD$，$F - ABC$，$F - ACE$的体积分别为$V_1$，$V_2$，$V_3$，则(　　　)

A.$V_1 = 2V_2$　　　　　　
　B.$V_1 = V_3$
C.$V_3 = V_1 + V_2$　　　　　
　D.$2V_3 = 3V_1$

答案：
11.CD　[命题点]三棱锥的体积、线面
　垂直的判定和性质
[深度解析]如图，连接BD交AC于
　0,连接OE,OF.设AB=ED=2FB=2,则
　　　　　　　　　　　　　　
AB=BC=CD=AD=2.由ED⊥平面
ABCD,FB//ED,得FB⊥平面ABCD,所
　以V=VE−ACD=$\frac{1}{3}$S△ACD.ED=$\frac{1}{3}$.
　$\frac{1}{2}$　.CD.ED=$\frac{1}{3}$x$\frac{1}{2}$x2×2×2=$\frac{4}{3}$,V=VF|A;C=$\frac{1}{3}$SABC.FB=
　$\frac{1}{3}$.$\frac{1}{2}$　.BC.FB=$\frac{1}{3}$x$\frac{1}{2}$x2×2×1=$\frac{2}{3}$(关键:求棱锥体积的关键是确定高，常常结合真线与平面的位置关系确定).ED⊥平面ABCD,ACC平面ABCD,所以ED⊥AC.又AC⊥BD,且ED∩BD=D,ED,BDC平面BDEF,所以AC⊥平面BDEF.又OFC平面BDEF,所以AC⊥OF.易知BD=2√2,OB=OD=$\sqrt{2}$,OF=　$\sqrt{OB²+FB²}$=　$\sqrt{3}$,OE=　　$\sqrt{OD²+ED²}$=　$\sqrt{6}$,EF=
　　$\sqrt{BD²+(ED−FB)²}$=　$\sqrt{(2√2)²+(2−1)²}$=3,所以EF²=OE²²+OF²,所以OF⊥OE,而OE∩AC=O,OE,ACC平面ACE,所以OF⊥平面ACE.又AC=AE=CE=2√2,所以V=V;−ACE=$\frac{1}{3}$SACE.OF=$\frac{1}{3}$.$\frac{√3}{4}$AC².OF=$\frac{1}{3}$$\frac{\sqrt{3}}{4}$x(2√2)²$\sqrt{3}$=2所以有V≠2V2,V≠V,V3=V+V,2V=3V,所以选项A,B不正确,选项C,D 正确，故选CD.