《2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版》

11. 如图是函数$y = \sin(\omega x + \varphi)$的部分图像，则$\sin(\omega x + \varphi)=$（ ）


A. $\sin(x + \frac{\pi}{3})$
B. $\sin(\frac{\pi}{3} - 2x)$
C. $\cos(2x + \frac{\pi}{6})$
D. $\cos(\frac{5\pi}{6} - 2x)$

答案： 11.BC　[命题点]三角函数的图像、性质及其解析式
[深度解析]由题图可知，最小正周期$T=\frac{2\pi}{|\omega|}=\frac{2\pi}{3}\times2=\frac{4\pi}{3}$，得$\omega=\pm\frac{3}{2}$，故A错误；当$\omega = \frac{3}{2}$时，将$(\frac{T}{6},A)$的坐标代入$y = A\sin(\omega x + \varphi)$，得$\frac{3}{2}\times\frac{T}{6}+\varphi=2k\pi+\frac{\pi}{2}$，$k\in Z$，即$\varphi=2k\pi+\frac{\pi}{2}-\frac{T}{4}$，因为$T = \frac{4\pi}{3}$，所以$\varphi=2k\pi+\frac{\pi}{2}-\frac{\pi}{3}=2k\pi+\frac{\pi}{6}$，$k\in Z$。当$k = 0$时，$\varphi=\frac{\pi}{6}$，则$y = A\sin(\frac{3}{2}x + \frac{\pi}{6})=A\sin(\pi - (\frac{3}{2}x + \frac{\pi}{6}))=A\sin(\frac{5\pi}{6}-\frac{3}{2}x)$，故B正确；$y = A\sin(\frac{3}{2}x + \frac{\pi}{6})=A\cos(\frac{\pi}{2}-(\frac{3}{2}x + \frac{\pi}{6}))=A\cos(\frac{\pi}{3}-\frac{3}{2}x)=A\cos(\frac{3}{2}x-\frac{\pi}{3})$，故C正确；$y = A\cos(\frac{3}{2}x-\frac{\pi}{3})=A\cos(\pi + (\frac{3}{2}x-\frac{\pi}{3}-\pi))=-A\cos(\frac{3}{2}x-\frac{4\pi}{3})$，故D错误。故选BC。
关键点拨：先根据周期求出$\omega$，再代入点的坐标求出$\varphi$，再根据诱导公式判断函数解析式的不同形式。

12. 已知$a＞0$，$b＞0$，且$a + b = 1$，则（ ）
A. $a² + b²\geq\frac{1}{2}$
B. $2^{a - b}＞\frac{1}{2}$
C. $\log_2a + \log_2b\geq - 2$
D. $\sqrt{a} + \sqrt{b}\leq\sqrt{2}$

答案： 12.ABD　[命题点]基本不等式的应用
[深度解析]由a＞0，b＞0，a + b = 1，得$\frac{a^{2}+b^{2}}{2}\geq(\frac{a + b}{2})^{2}=\frac{1}{4}$，即a² + b²≥$\frac{1}{2}$，当且仅当a = b = $\frac{1}{2}$时取等号，故A正确；由a＞0，b＞0，a + b = 1，得a - b = 2a - 1＞ - 1，故$2^{a - b}＞\frac{1}{2}$，故B正确；$\log_{2}a+\log_{2}b=\log_{2}(ab)\leq\log_{2}(\frac{a + b}{2})^{2}=\log_{2}(\frac{1}{2})^{2}=-2$，当且仅当a = b = $\frac{1}{2}$时，等号成立，故C错误（另解：令a = $\frac{1}{4}$，b = $\frac{3}{4}$，则$\log_{2}\frac{1}{4}+\log_{2}\frac{3}{4}＜ - 2$，故C错误）；$(\sqrt{a}+\sqrt{b})^{2}=a + b + 2\sqrt{ab}=1 + 2\sqrt{ab}\leq1 + a + b = 2$，得$\sqrt{a}+\sqrt{b}\leq\sqrt{2}$，当且仅当a = b = $\frac{1}{2}$时，等号成立，故D正确。故选ABD。
方法速记：灵活利用基本不等式的变形，掌握$ab\leq(\frac{a + b}{2})^{2}\leq\frac{a^{2}+b^{2}}{2}$。

13. 棱长为$2$的正方体$ABCD - A_1B_1C_1D_1$中，$M$，$N$分别为棱$BB_1$，$AB$的中点，则三棱锥$A_1 - DMN$的体积为______。

答案：
13.1　[命题点]三棱锥的体积
[深度解析]如图，因为正方体ABCD - A₁B₁C₁D₁中，DA⊥平面A₁ABB₁，所以DA⊥平面AMN。
所以$V_{A - DMN}=V_{D - AMN}=\frac{1}{3}\cdot S_{\triangle AMN}\cdot AD=\frac{1}{3}\times(2\times2-\frac{1}{2}\times1\times2 - \frac{1}{2}\times1\times1)\times2=\frac{1}{3}\times\frac{3}{2}\times2 = 1$。

14. 斜率为$\sqrt{3}$的直线过抛物线$C:y² = 4x$的焦点，且与$C$交于$A$，$B$两点，则$\vert AB\vert=$______。

答案： 14.$\frac{16}{3}$　[命题点]直线与抛物线的位置关系及弦长
[深度解析]由y² = 4x，得其焦点F(1,0)。又直线AB的斜率为$\sqrt{3}$，所以直线AB的方程为$y = \sqrt{3}(x - 1)$。联立$\begin{cases}y^{2}=4x\\y = \sqrt{3}(x - 1)\end{cases}$，得$3x^{2}-10x + 3 = 0$，设A(xₐ,yₐ)，B(x_b,y_b)，则$x_{A}+x_{B}=\frac{10}{3}$。又$|AF|=x_{A}+1$，$|BF|=x_{B}+1$（提示：利用抛物线定义表示$|AF|$，$|BF|$），所以$|AB|=|AF|+|BF|=x_{A}+x_{B}+2=\frac{10}{3}+2=\frac{16}{3}$。
方法速记：若直线与抛物线$y^{2}=2px(p\gt0)$交于A(xₐ,yₐ)，B(x_b,y_b)两点，则$|AB|=x_{A}+x_{B}+p$。

15. 将数列$\{2n - 1\}$与$\{3n - 2\}$的公共项从小到大排列得到数列$\{a_n\}$，则$\{a_n\}$的前$n$项和为______。

答案： 15.3n² - 2n　[命题点]等差数列求和
[深度解析]数列{2n - 1}表示首项为1，公差为2的等差数列，各项均为正奇数，而数列{3n - 2}表示首项为1，公差为3的等差数列，各项分别为交替出现的正奇数与正偶数，它们的公共项为数列{3n - 2}中的奇数项，所以{aₙ}是首项为1，公差为6的等差数列，其前n项和$S_{n}=n\times1+\frac{n(n - 1)}{2}\times6=3n^{2}-2n$。
易错警示：注意公差的改变。

16. 某中学开展劳动实习，学生加工制作零件，零件的截面如图所示。O为圆孔及轮廓圆弧AB所在圆的圆心，A是圆弧AB与直线AG的切点，B是圆弧AB与直线BC的切点，四边形DEFG为矩形，BC⊥DG，垂足为C，tan∠ODC = $\frac{3}{5}$，BH//DG，EF = 12cm，DE = 2cm，A到直线DE和EF的距离均为7cm，圆孔半径为1cm，则图中阴影部分的面积为________cm².

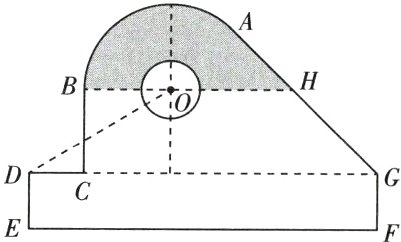
答案：
$\frac{5\pi}{2} + 4$ [命题点]三角形与扇形面积的应用
[深度解析]连接 OA，过点 A 作 EF 的垂线，分别交 BH，DG 于点 M，N，过点 O 作垂直于 CG 的直线与 CG 交于点 P。则由 EF = 12，DE = 2，A 到直线 DE 和 EF 的距离为 7 可知 AN = NG = 5，则∠MAH = $\frac{\pi}{4}$。又 OA⊥AG，所以△AOM 为等腰直角三角形，∠AOM = $\frac{\pi}{4}$，∠AOB = $\frac{3\pi}{4}$。令 AM = OM = MH = PN = x，则 OP = MN = 5 - x，DP = 7 - x，OA = AH = $\sqrt{2}x$。由 tan∠ODC = $\frac{OP}{DP}$ = $\frac{5 - x}{7 - x}$ = $\frac{3}{5}$，得 x = 2，则 OA = 2$\sqrt{2}$。所以$S_{\triangle OAH}$ = $\frac{1}{2}$·OA·AH = 4，$S_{扇形 OAB}$ = $\frac{1}{2}$×$\frac{3\pi}{4}$×$OA^2$ = $\frac{3\pi}{8}$×8 = 3π，圆孔半径为 1，则$S_{半圆}$ = $\frac{1}{2}$π×$1^2$ = $\frac{\pi}{2}$，所以$S_{阴影}$ = $S_{扇形 OAB}$ + $S_{\triangle OAH}$ - $S_{半圆}$ = 3π + 4 - $\frac{\pi}{2}$ = $\frac{5\pi}{2}$ + 4。

关键点拨：求出圆的半径，结合三角形求出圆心角，以便求扇形面积，通过间接法求解。

17. (本小题满分10分) 在①ac = $\sqrt{3}$，②csinA = 3，③c = $\sqrt{3}$b这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求c的值；若问题中的三角形不存在，说明理由。
问题: 是否存在△ABC，它的内角A，B，C的对边分别为a，b，c，且sinA = $\sqrt{3}$sinB，C = $\frac{\pi}{6}$，________?
注: 如果选择多个条件分别解答，按第一个解答计分。

答案： [命题点]利用正弦定理、余弦定理解三角形
[解]方案一：选条件①
由 C = $\frac{\pi}{6}$和余弦定理得$\frac{a^2 + b^2 - c^2}{2ab}$ = $\frac{\sqrt{3}}{2}$。 3 分
由 sinA = $\sqrt{3}$sinB 及正弦定理得 a = $\sqrt{3}$b。 5 分
于是$\frac{3b^2 + b^2 - c^2}{2\sqrt{3}b^2}$ = $\frac{\sqrt{3}}{2}$，由此可得 b = c。 8 分
由① ac = $\sqrt{3}$，解得 a = $\sqrt{3}$，b = c = 1。 9 分
因此，选条件①时问题中的三角形存在，此时 c = 1。 10 分
方案二：选条件②
由 C = $\frac{\pi}{6}$和余弦定理得$\frac{a^2 + b^2 - c^2}{2ab}$ = $\frac{\sqrt{3}}{2}$。 3 分
由 sinA = $\sqrt{3}$sinB 及正弦定理得 a = $\sqrt{3}$b。 5 分
于是$\frac{3b^2 + b^2 - c^2}{2\sqrt{3}b^2}$ = $\frac{\sqrt{3}}{2}$，由此可得 b = c，B = C = $\frac{\pi}{6}$，A = $\frac{2\pi}{3}$。
由② csinA = 3，得 c = b = 2$\sqrt{3}$，a = 6。 8 分
因此，选条件②时问题中的三角形存在。 9 分
此时 c = 2$\sqrt{3}$。 10 分
方案三：选条件③
由 C = $\frac{\pi}{6}$和余弦定理得$\frac{a^2 + b^2 - c^2}{2ab}$ = $\frac{\sqrt{3}}{2}$。 3 分
由 sinA = $\sqrt{3}$sinB 及正弦定理得 a = $\sqrt{3}$b。 5 分
于是$\frac{3b^2 + b^2 - c^2}{2\sqrt{3}b^2}$ = $\frac{\sqrt{3}}{2}$，由此可得 b = c。 8 分
由③ c = $\sqrt{3}$b，与 b = c 矛盾。 9 分
因此，选条件③时问题中的三角形不存在。 10 分

18. (本小题满分12分) 已知公比大于1的等比数列{aₙ}满足a₂² + a₄ = 20，a₃ = 8。
(1) 求{aₙ}的通项公式；
(2) 求a₁a₂ - a₂a₃ +... + (-1)ⁿ⁻¹aₙaₙ₊₁。

答案： [命题点]等比数列的通项公式及前 n 项和公式
[解]
(1)设$\{a_n\}$的公比为 q。由题设得$aq + aq^2 = 20$，$aq^2 = 8$，
解得 q = $\frac{1}{2}$(舍去)，q = 2。 3 分
则 a = 2。
所以$\{a_n\}$的通项公式为$a_n = 2^n$。 5 分
(2)由
(1)可知$(-1)^{n - 1}a_na_{n + 1} = (-1)^{n - 1}·2^n·2^{n + 1} = (-1)^{n - 1}2^{2n + 1}$。 6 分
则$a_1a_2 - a_2a_3 + \cdots + (-1)^{n - 1}a_na_{n + 1}$
= $2^3 - 2^5 + 2^7 - 2^9 + \cdots + (-1)^{n - 1}·2^{2n + 1}$
= $\frac{2^3[1 - (-2^2)^n]}{1 - (-2^2)}$ = $\frac{8}{5} - (-1)^n\frac{2^{2n + 3}}{5}$。 12 分