2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年理想树图书高考必刷卷42套模拟卷汇编高中数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
18.(本小题满分12分)在四棱锥$P - ABCD$中,$PD\perp$底面$ABCD$,$CD// AB$,$AD = DC = CB = 1$,$AB = 2$,$DP = \sqrt{3}$.
(1)证明:$BD\perp PA$;
(2)求$PD$与平面$PAB$所成的角的正弦值.

答案:
18.[命题点]异面直线垂直的证明和直线与平面所成角的正弦值的求解
(1)[证明]因为$PD\perp$底面$ABCD$,$BD\subset$底面$ABCD$,
所以$PD\perp BD$。
取$AB$的中点$E$,连接$DE$。
因为$CD// AB$,$CD = EB$,所以四边形$BCDE$为平行四边形,所以$ED = BC = 1$,所以$DE = \frac{1}{2}AB = 1$,所以$\triangle ABD$是直角三角形,且$BD\perp AD$。3分
因为$PD\cap AD = D$,所以$BD\perp$平面$PAD$,又$PA\subset$平面$PAD$,所以$BD\perp PA$。5分
一题多解
因为$BD = \sqrt{3}$,又因为$AB = 2$,$AD = 1$,从而$AB^2 = AD^2 + BD^2$,故$BD\perp AD$。3分
因为$PD\perp$底面$ABCD$,所以$BD\perp PD$。又$AD\cap PD = D$,所以$BD\perp$平面$PAD$。因为$PA\subset$平面$PAD$,所以$BD\perp PA$。5分
(2)[解]解法一:由
(1)可知,$PD$,$AD$,$BD$两两垂直,$BD = \sqrt{AB^2 - AD^2} = \sqrt{3}$
分别以$DA$,$DB$,$DP$所在直线为$x$,$y$,$z$轴建立空间直角坐标系,如图,则$D(0,0,0)$,$A(1,0,0)$,$B(0,\sqrt{3},0)$,$P(0,0,\sqrt{3})$,
所以$\overrightarrow{PD}=(0,0,-\sqrt{3})$,$\overrightarrow{PA}=(1,0,-\sqrt{3})$,$\overrightarrow{AB}=(-1,\sqrt{3},0)$。7分
设平面$PAB$的法向量为$\overrightarrow{n}=(x,y,z)$,
则$\begin{cases}\overrightarrow{n}\cdot\overrightarrow{AP}=0\\\overrightarrow{n}\cdot\overrightarrow{AB}=0\end{cases}$,即$\begin{cases}-x + \sqrt{3}z = 0\\-x + \sqrt{3}y = 0\end{cases}$,
不妨设$z = 1$,则$\overrightarrow{n}=(\sqrt{3},1,1)$。
设$PD$与平面$PAB$所成的角为$\theta$,
所以$\sin\theta = |\cos\langle\overrightarrow{PD},\overrightarrow{n}\rangle| = \frac{|\overrightarrow{PD}\cdot\overrightarrow{n}|}{|\overrightarrow{PD}|\cdot|\overrightarrow{n}|} = \frac{|-\sqrt{3}|}{\sqrt{3}\cdot\sqrt{5}} = \frac{\sqrt{5}}{5}$,
所以$PD$与平面$PAB$所成的角的正弦值为$\frac{\sqrt{5}}{5}$。12分
解法二:由题设及第
(1)问得三棱锥$P - ABD$的体积$V = \frac{1}{3}\times\frac{1}{2}\times1\times\sqrt{3}\times\sqrt{3} = \frac{1}{2}$。6分
又$AB = 2$,$PA = \sqrt{DA^2 + DP^2} = 2$,$PB = \sqrt{DB^2 + DP^2} = \sqrt{6}$,所以
$\cos\angle PAB = \frac{AB^2 + PA^2 - PB^2}{2\times AB\times PA} = \frac{4 + 4 - 6}{2\times 2\times 2} = \frac{1}{4}$,所以$\sin\angle PAB = \frac{\sqrt{15}}{4}$。8分
设点$D$到平面$PAB$的距离为$d$,则$V = \frac{1}{3}\times\frac{1}{2}\times2\times2\times\frac{\sqrt{15}}{4}\times d = \frac{\sqrt{15}}{6}d$。10分
由$\frac{\sqrt{15}}{6}d = \frac{1}{2}$,得$d = \frac{\sqrt{15}}{5}$。
因此$PD$与平面$PAB$所成角的正弦值为$\frac{d}{PD} = \frac{\frac{\sqrt{15}}{5}}{\sqrt{3}} = \frac{\sqrt{5}}{5}$。12分
解法三:如图所示,作$DE\perp AB$,垂足为$E$,连接$PE$。
因为$PD\perp$底面$ABCD$,所以$PD\perp AB$,因为$PD\cap DE = D$,所以$AB\perp$平面$PDE$。
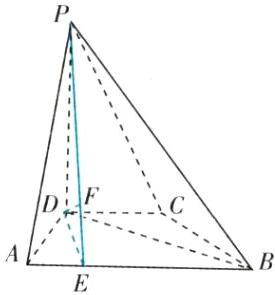
作$DF\perp PE$,垂足为$F$;因为$AB\perp$平面$PDE$,$DF\subset$平面$PDE$,所以$DF\perp AB$。
因为$AB\cap PE = E$,所以$DF\perp$平面$PAB$。
因此$\angle DPF$即为$PD$与平面$PAB$所成的角。8分
因为$\frac{1}{2}\times AB\times DE = \frac{1}{2}\times DA\times DB$,所以$DE = \frac{\sqrt{3}}{2}$,故$PE = \sqrt{DE^2 + DP^2} = \sqrt{\frac{3}{4} + 3} = \frac{\sqrt{15}}{2}$。10分
因此$PD$与平面$PAB$所成角的正弦值为$\frac{DE}{PE} = \frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{15}}{2}} = \frac{\sqrt{5}}{5}$。12分
18.[命题点]异面直线垂直的证明和直线与平面所成角的正弦值的求解
(1)[证明]因为$PD\perp$底面$ABCD$,$BD\subset$底面$ABCD$,
所以$PD\perp BD$。
取$AB$的中点$E$,连接$DE$。
因为$CD// AB$,$CD = EB$,所以四边形$BCDE$为平行四边形,所以$ED = BC = 1$,所以$DE = \frac{1}{2}AB = 1$,所以$\triangle ABD$是直角三角形,且$BD\perp AD$。3分
因为$PD\cap AD = D$,所以$BD\perp$平面$PAD$,又$PA\subset$平面$PAD$,所以$BD\perp PA$。5分
一题多解
因为$BD = \sqrt{3}$,又因为$AB = 2$,$AD = 1$,从而$AB^2 = AD^2 + BD^2$,故$BD\perp AD$。3分
因为$PD\perp$底面$ABCD$,所以$BD\perp PD$。又$AD\cap PD = D$,所以$BD\perp$平面$PAD$。因为$PA\subset$平面$PAD$,所以$BD\perp PA$。5分
(2)[解]解法一:由
(1)可知,$PD$,$AD$,$BD$两两垂直,$BD = \sqrt{AB^2 - AD^2} = \sqrt{3}$
分别以$DA$,$DB$,$DP$所在直线为$x$,$y$,$z$轴建立空间直角坐标系,如图,则$D(0,0,0)$,$A(1,0,0)$,$B(0,\sqrt{3},0)$,$P(0,0,\sqrt{3})$,
所以$\overrightarrow{PD}=(0,0,-\sqrt{3})$,$\overrightarrow{PA}=(1,0,-\sqrt{3})$,$\overrightarrow{AB}=(-1,\sqrt{3},0)$。7分
设平面$PAB$的法向量为$\overrightarrow{n}=(x,y,z)$,
则$\begin{cases}\overrightarrow{n}\cdot\overrightarrow{AP}=0\\\overrightarrow{n}\cdot\overrightarrow{AB}=0\end{cases}$,即$\begin{cases}-x + \sqrt{3}z = 0\\-x + \sqrt{3}y = 0\end{cases}$,
不妨设$z = 1$,则$\overrightarrow{n}=(\sqrt{3},1,1)$。
设$PD$与平面$PAB$所成的角为$\theta$,
所以$\sin\theta = |\cos\langle\overrightarrow{PD},\overrightarrow{n}\rangle| = \frac{|\overrightarrow{PD}\cdot\overrightarrow{n}|}{|\overrightarrow{PD}|\cdot|\overrightarrow{n}|} = \frac{|-\sqrt{3}|}{\sqrt{3}\cdot\sqrt{5}} = \frac{\sqrt{5}}{5}$,
所以$PD$与平面$PAB$所成的角的正弦值为$\frac{\sqrt{5}}{5}$。12分
解法二:由题设及第
(1)问得三棱锥$P - ABD$的体积$V = \frac{1}{3}\times\frac{1}{2}\times1\times\sqrt{3}\times\sqrt{3} = \frac{1}{2}$。6分
又$AB = 2$,$PA = \sqrt{DA^2 + DP^2} = 2$,$PB = \sqrt{DB^2 + DP^2} = \sqrt{6}$,所以
$\cos\angle PAB = \frac{AB^2 + PA^2 - PB^2}{2\times AB\times PA} = \frac{4 + 4 - 6}{2\times 2\times 2} = \frac{1}{4}$,所以$\sin\angle PAB = \frac{\sqrt{15}}{4}$。8分
设点$D$到平面$PAB$的距离为$d$,则$V = \frac{1}{3}\times\frac{1}{2}\times2\times2\times\frac{\sqrt{15}}{4}\times d = \frac{\sqrt{15}}{6}d$。10分
由$\frac{\sqrt{15}}{6}d = \frac{1}{2}$,得$d = \frac{\sqrt{15}}{5}$。
因此$PD$与平面$PAB$所成角的正弦值为$\frac{d}{PD} = \frac{\frac{\sqrt{15}}{5}}{\sqrt{3}} = \frac{\sqrt{5}}{5}$。12分
解法三:如图所示,作$DE\perp AB$,垂足为$E$,连接$PE$。
因为$PD\perp$底面$ABCD$,所以$PD\perp AB$,因为$PD\cap DE = D$,所以$AB\perp$平面$PDE$。

作$DF\perp PE$,垂足为$F$;因为$AB\perp$平面$PDE$,$DF\subset$平面$PDE$,所以$DF\perp AB$。
因为$AB\cap PE = E$,所以$DF\perp$平面$PAB$。
因此$\angle DPF$即为$PD$与平面$PAB$所成的角。8分
因为$\frac{1}{2}\times AB\times DE = \frac{1}{2}\times DA\times DB$,所以$DE = \frac{\sqrt{3}}{2}$,故$PE = \sqrt{DE^2 + DP^2} = \sqrt{\frac{3}{4} + 3} = \frac{\sqrt{15}}{2}$。10分
因此$PD$与平面$PAB$所成角的正弦值为$\frac{DE}{PE} = \frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{15}}{2}} = \frac{\sqrt{5}}{5}$。12分
19.(本小题满分12分)甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得10分,负方得0 分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立.
(1)求甲学校获得冠军的概率;
(2)用X表示乙学校的总得分,求X的分布列与期望
答案:
19.[命题点]相互独立事件的概率、离散型随机变量的分布列和期望
[解]
(1)记甲学校获得冠军的事件为A,则P(A)=0.5×0.4×(1 - 0.8)+0.5×(1 - 0.4)×0.8+(1 - 0.5)×0.4×0.8+0.5×0.4×0.8 = 0.6. 4分
(2)依题意,X的可能取值为0,10,20,30.
依题意,P(X = 0)=0.5×0.4×0.8 = 0.16,
P(X = 10)=0.5×0.4×(1 - 0.8)+0.5×(1 - 0.4)×0.8+(1 - 0.5)×0.4×0.8 = 0.44,
P(X = 20)=0.5×(1 - 0.4)×(1 - 0.8)+(1 - 0.5)×(1 - 0.4)×0.8+(1 - 0.5)×0.4×(1 - 0.8)=0.34,
P(X = 30)=(1 - 0.5)×(1 - 0.4)×(1 - 0.8)=0.06. 9分
所以X的分布列为

所以X的期望E(X)=0×0.16 + 10×0.44+20×0.34 + 30×0.06 = 13. 12分
19.[命题点]相互独立事件的概率、离散型随机变量的分布列和期望
[解]
(1)记甲学校获得冠军的事件为A,则P(A)=0.5×0.4×(1 - 0.8)+0.5×(1 - 0.4)×0.8+(1 - 0.5)×0.4×0.8+0.5×0.4×0.8 = 0.6. 4分
(2)依题意,X的可能取值为0,10,20,30.
依题意,P(X = 0)=0.5×0.4×0.8 = 0.16,
P(X = 10)=0.5×0.4×(1 - 0.8)+0.5×(1 - 0.4)×0.8+(1 - 0.5)×0.4×0.8 = 0.44,
P(X = 20)=0.5×(1 - 0.4)×(1 - 0.8)+(1 - 0.5)×(1 - 0.4)×0.8+(1 - 0.5)×0.4×(1 - 0.8)=0.34,
P(X = 30)=(1 - 0.5)×(1 - 0.4)×(1 - 0.8)=0.06. 9分
所以X的分布列为

所以X的期望E(X)=0×0.16 + 10×0.44+20×0.34 + 30×0.06 = 13. 12分
20.(本小题满分12分)设抛物线C:y²=2px(p>0)的焦点为F,点D(p,0),过F的直线交C于M,N两点.
当直线MD垂直于x轴时,|MF|=3.
(1)求C的方程;
(2)设直线MD,ND与C的另一个交点分别为A,B,记直线MN,AB的倾斜角分别为α,β.当α−β取得最大值时,求直线AB的方程.
答案:
20.思路导引
(1)利用抛物线的定义求得p,即得C的方程;
(2)设出点M,N,A,B的坐标及直线MN:x = my + 1,联立直线MN与C的方程→点M,N纵坐标间的关系→当直线MN的斜率存在时,求得kMN、kAB→直线MD的方程→与抛物线的方程联立根与系数的关系kAB = $\frac{k_{MN}}{2}$→设kMN = 2kAB = 2k>0,利用两角差的正切公式求(α - β)的最大值→kAB→设直线AB的方程,与C的方程联立,结合根与系数的关系求解.
[命题点]抛物线的定义及方程、直线与抛物线的位置关系、抛物线中的最值问题
[解]
(1)由题知,当MD⊥x轴时,xM = p,从而|MF| = xM + $\frac{p}{2}$ = $\frac{3p}{2}$ = 3,解得p = 2,故C的方程为y² = 4x. 3分
(2)设M($\frac{y_1^2}{4}$,y1),N($\frac{y_2^2}{4}$,y2),A($\frac{y_3^2}{4}$,y3),B($\frac{y_4^2}{4}$,y4),直线MN:x = my + 1.
(当直线的斜率不能为0时,可设直线方程为x = ty + c,这样可以避免讨论直线斜率是否存在)
联立$\begin{cases}x = my + 1\\y^2 = 4x\end{cases}$得y² - 4my - 4 = 0,△>0,y1y2 = - 4. 5分
当直线MN的斜率不存在时,易知直线AB的斜率也不存在,此时α - β = 0.
当直线MN的斜率存在时,kMN = $\frac{y_1 - y_2}{\frac{y_1^2}{4} - \frac{y_2^2}{4}}$ = $\frac{4}{y_1 + y_2}$,kAB = $\frac{y_3 - y_4}{\frac{y_3^2}{4} - \frac{y_4^2}{4}}$ = $\frac{4}{y_3 + y_4}$. 7分
直线MD:x = $\frac{4}{y_1}$y + 2,与抛物线方程联立可得y² - y - 8 = 0,△2>0,y1y3 = - 8,所以y3 = - $\frac{8}{y_1}$,
y - 8 = 0,△2>0,y1y3 = - 8,所以y3 = - $\frac{8}{y_1}$,
同理可得y4 = - $\frac{8}{y_2}$,
(利用抛物线方程对斜率进行化简,利用根与系数的关系得出坐标间的关系)
所以kAB = $\frac{4}{y_3 + y_4}$ = $\frac{4}{- \frac{8}{y_1} - \frac{8}{y_2}}$ = $\frac{4}{- \frac{8(y_1 + y_2)}{y_1y_2}}$ = $\frac{4}{- \frac{8(y_1 + y_2)}{- 4}}$ = $\frac{k_{MN}}{2}$. 9分
又直线MN,AB的倾斜角分别为α,β,
所以kAB = tanβ = $\frac{k_{MN}}{2}$ = $\frac{tanα}{2}$
要使α - β最大,则β∈(0,$\frac{\pi}{2}$).
设kMN = 2kAB = 2k>0,则tan(α - β) = $\frac{tanα - tanβ}{1 + tanαtanβ}$ = $\frac{k}{1 + 2k^2}$ = $\frac{1}{\frac{1}{k} + 2k}$ ≤ $\frac{1}{2\sqrt{\frac{1}{k} \cdot 2k}}$ = $\frac{\sqrt{2}}{4}$,
当且仅当$\frac{1}{k}$ = 2k,即k = $\frac{\sqrt{2}}{2}$时,等号成立,
所以当α - β最大时,kAB = $\frac{\sqrt{2}}{2}$.设直线AB:x = $\sqrt{2}$y + n,
与抛物线方程联立可得y² - 4$\sqrt{2}$y - 4n = 0.
△3 = 32 + 16n>0,得n> - 2.
y3y4 = - 4n = 4y1y2 = - 16,所以n = 4,
所以直线AB的方程为x - $\sqrt{2}$y - 4 = 0. 12分
另一种解法:
(1)设抛物线上点的坐标为(p,y0),代入抛物线方程得y0² = 2p².
因为F($\frac{p}{2}$,0),|MF| = 3,所以$\sqrt{(p - \frac{p}{2})^2 + y_0^2}$ = 3,即$\sqrt{(\frac{p}{2})^2 + 2p^2}$ = 3,解得p = 2,
故C的方程为y² = 4x. 3分
(2)当直线MN的斜率不存在时,易知直线AB的斜率也不存在,此时α - β = 0.
当直线MN的斜率存在时,设kMN = k1 = tanα,kAB = k2 = tanβ,则tan(α - β) = $\frac{k_1 - k_2}{1 + k_1k_2}$. 5分
不妨设M(x1,y1),N(x2,y2)(y1>0,y2<0),A(x3,y3),B(x4,y4)(y3<0,y4>0),直线AB:y = k2(x - m)(m>0).
由$\begin{cases}y = k_1(x - 1)\\y^2 = 4x\end{cases}$得k_1^2x^2 - (2k_1^2 + 4)x + k_1^2 = 0,则x1x2 = 1.
由$\begin{cases}y = k_2(x - m)\\y^2 = 4x\end{cases}$得k_2^2x^2 - (2k_2^2m + 4)x + k_2^2m^2 = 0,则x3x4 = m².
由$\begin{cases}y = k_{MN}(x - 2)\\y^2 = 4x\end{cases}$得k_{MN}^2x^2 - (4k_{MN}^2 + 4)x + 4k_{MN}^2 = 0,则x1x2 = 1. 8分
所以M(x1,2$\sqrt{x_1}$),N($\frac{1}{x_1}$,- 2$\sqrt{x_1}$),A($\frac{4}{x_1}$,- $\frac{4}{\sqrt{x_1}}$),B(4x1,4$\sqrt{x_1}$),所以k1 = $\frac{2\sqrt{x_1}}{x_1 - 1}$,k2 = $\frac{\sqrt{x_1}}{x_1 - 1}$,所以k1 = 2k2,
要使α - β最大,则k2>0,
所以tan(α - β) = $\frac{k_1 - k_2}{1 + k_1k_2}$ = $\frac{k_2}{1 + 2k_2^2}$ = $\frac{1}{\frac{1}{k_2} + 2k_2}$ ≤ $\frac{1}{2\sqrt{\frac{1}{k_2} \cdot 2k_2}}$ = $\frac{\sqrt{2}}{4}$,
当且仅当$\frac{1}{k_2}$ = 2k_2,即k2 = $\frac{\sqrt{2}}{2}$时,等号成立,α - β最大.
易得x3x4 = 16 = m²,所以m = 4(负值舍去),所以直线AB的方程为x - $\sqrt{2}$y - 4 = 0. 12分
20.思路导引
(1)利用抛物线的定义求得p,即得C的方程;
(2)设出点M,N,A,B的坐标及直线MN:x = my + 1,联立直线MN与C的方程→点M,N纵坐标间的关系→当直线MN的斜率存在时,求得kMN、kAB→直线MD的方程→与抛物线的方程联立根与系数的关系kAB = $\frac{k_{MN}}{2}$→设kMN = 2kAB = 2k>0,利用两角差的正切公式求(α - β)的最大值→kAB→设直线AB的方程,与C的方程联立,结合根与系数的关系求解.
[命题点]抛物线的定义及方程、直线与抛物线的位置关系、抛物线中的最值问题
[解]
(1)由题知,当MD⊥x轴时,xM = p,从而|MF| = xM + $\frac{p}{2}$ = $\frac{3p}{2}$ = 3,解得p = 2,故C的方程为y² = 4x. 3分
(2)设M($\frac{y_1^2}{4}$,y1),N($\frac{y_2^2}{4}$,y2),A($\frac{y_3^2}{4}$,y3),B($\frac{y_4^2}{4}$,y4),直线MN:x = my + 1.
(当直线的斜率不能为0时,可设直线方程为x = ty + c,这样可以避免讨论直线斜率是否存在)
联立$\begin{cases}x = my + 1\\y^2 = 4x\end{cases}$得y² - 4my - 4 = 0,△>0,y1y2 = - 4. 5分
当直线MN的斜率不存在时,易知直线AB的斜率也不存在,此时α - β = 0.
当直线MN的斜率存在时,kMN = $\frac{y_1 - y_2}{\frac{y_1^2}{4} - \frac{y_2^2}{4}}$ = $\frac{4}{y_1 + y_2}$,kAB = $\frac{y_3 - y_4}{\frac{y_3^2}{4} - \frac{y_4^2}{4}}$ = $\frac{4}{y_3 + y_4}$. 7分
直线MD:x = $\frac{4}{y_1}$y + 2,与抛物线方程联立可得y² -
 y - 8 = 0,△2>0,y1y3 = - 8,所以y3 = - $\frac{8}{y_1}$,
y - 8 = 0,△2>0,y1y3 = - 8,所以y3 = - $\frac{8}{y_1}$,同理可得y4 = - $\frac{8}{y_2}$,
(利用抛物线方程对斜率进行化简,利用根与系数的关系得出坐标间的关系)
所以kAB = $\frac{4}{y_3 + y_4}$ = $\frac{4}{- \frac{8}{y_1} - \frac{8}{y_2}}$ = $\frac{4}{- \frac{8(y_1 + y_2)}{y_1y_2}}$ = $\frac{4}{- \frac{8(y_1 + y_2)}{- 4}}$ = $\frac{k_{MN}}{2}$. 9分
又直线MN,AB的倾斜角分别为α,β,
所以kAB = tanβ = $\frac{k_{MN}}{2}$ = $\frac{tanα}{2}$
要使α - β最大,则β∈(0,$\frac{\pi}{2}$).
设kMN = 2kAB = 2k>0,则tan(α - β) = $\frac{tanα - tanβ}{1 + tanαtanβ}$ = $\frac{k}{1 + 2k^2}$ = $\frac{1}{\frac{1}{k} + 2k}$ ≤ $\frac{1}{2\sqrt{\frac{1}{k} \cdot 2k}}$ = $\frac{\sqrt{2}}{4}$,
当且仅当$\frac{1}{k}$ = 2k,即k = $\frac{\sqrt{2}}{2}$时,等号成立,
所以当α - β最大时,kAB = $\frac{\sqrt{2}}{2}$.设直线AB:x = $\sqrt{2}$y + n,
与抛物线方程联立可得y² - 4$\sqrt{2}$y - 4n = 0.
△3 = 32 + 16n>0,得n> - 2.
y3y4 = - 4n = 4y1y2 = - 16,所以n = 4,
所以直线AB的方程为x - $\sqrt{2}$y - 4 = 0. 12分
另一种解法:
(1)设抛物线上点的坐标为(p,y0),代入抛物线方程得y0² = 2p².
因为F($\frac{p}{2}$,0),|MF| = 3,所以$\sqrt{(p - \frac{p}{2})^2 + y_0^2}$ = 3,即$\sqrt{(\frac{p}{2})^2 + 2p^2}$ = 3,解得p = 2,
故C的方程为y² = 4x. 3分
(2)当直线MN的斜率不存在时,易知直线AB的斜率也不存在,此时α - β = 0.
当直线MN的斜率存在时,设kMN = k1 = tanα,kAB = k2 = tanβ,则tan(α - β) = $\frac{k_1 - k_2}{1 + k_1k_2}$. 5分
不妨设M(x1,y1),N(x2,y2)(y1>0,y2<0),A(x3,y3),B(x4,y4)(y3<0,y4>0),直线AB:y = k2(x - m)(m>0).
由$\begin{cases}y = k_1(x - 1)\\y^2 = 4x\end{cases}$得k_1^2x^2 - (2k_1^2 + 4)x + k_1^2 = 0,则x1x2 = 1.
由$\begin{cases}y = k_2(x - m)\\y^2 = 4x\end{cases}$得k_2^2x^2 - (2k_2^2m + 4)x + k_2^2m^2 = 0,则x3x4 = m².
由$\begin{cases}y = k_{MN}(x - 2)\\y^2 = 4x\end{cases}$得k_{MN}^2x^2 - (4k_{MN}^2 + 4)x + 4k_{MN}^2 = 0,则x1x2 = 1. 8分
所以M(x1,2$\sqrt{x_1}$),N($\frac{1}{x_1}$,- 2$\sqrt{x_1}$),A($\frac{4}{x_1}$,- $\frac{4}{\sqrt{x_1}}$),B(4x1,4$\sqrt{x_1}$),所以k1 = $\frac{2\sqrt{x_1}}{x_1 - 1}$,k2 = $\frac{\sqrt{x_1}}{x_1 - 1}$,所以k1 = 2k2,
要使α - β最大,则k2>0,
所以tan(α - β) = $\frac{k_1 - k_2}{1 + k_1k_2}$ = $\frac{k_2}{1 + 2k_2^2}$ = $\frac{1}{\frac{1}{k_2} + 2k_2}$ ≤ $\frac{1}{2\sqrt{\frac{1}{k_2} \cdot 2k_2}}$ = $\frac{\sqrt{2}}{4}$,
当且仅当$\frac{1}{k_2}$ = 2k_2,即k2 = $\frac{\sqrt{2}}{2}$时,等号成立,α - β最大.
易得x3x4 = 16 = m²,所以m = 4(负值舍去),所以直线AB的方程为x - $\sqrt{2}$y - 4 = 0. 12分
查看更多完整答案,请扫码查看


