《2026年全品中考复习方案数学北师大版》

3. 在 $\triangle ABC$ 中，$\angle ABC = 60°$，$AB = 4$，$AC = \sqrt{13}$，则 $BC =$3或1.

答案： 3.3或1

4. 思维能力 一题多解(2024 深圳)如图 20-8，在 $\triangle ABC$ 中，$AB = BC$，$\tan B = \frac{5}{12}$. $D$ 为 $BC$ 上一点，且满足 $\frac{BD}{CD} = \frac{8}{5}$，过点 $D$ 作 $DE \perp AD$ 交 $AC$ 的延长线于点 $E$，则 $\frac{CE}{AC} =$$\frac{20}{21}$.

答案： 4.$\frac{20}{21}$

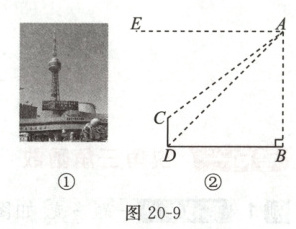
例 3（2024 吉林）图 20-9①中的吉林省广播电视塔，又称“吉塔”. 某直升机于空中 $A$ 处探测到吉塔，此时飞行高度 $AB = 873$ m，如图②. 从直升机上看塔尖 $C$ 的俯角 $\angle EAC = 37°$，看塔底 $D$ 的俯角 $\angle EAD = 45°$，求吉塔的高度 $CD$（结果精确到 $0.1$ m）.
（参考数据：$\sin 37° \approx 0.60$，$\cos 37° \approx 0.80$，
$\tan 37° \approx 0.75$）

答案： 例3　约为218.3m

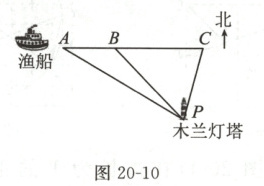
例 4(2025 临沂模拟)木兰灯塔是亚洲最高、世界第二高的航标灯塔，位于海南岛的最北端，是海南岛东北部最重要的航标. 某天，一艘渔船自西向东(沿 $AC$ 方向)以 10 海里/时的速度在琼州海峡航行，如图 20-10 所示.
航行记录
记录一：上午 8 时，渔船到达木兰灯塔 $P$ 北偏西 $60°$ 方向上的 $A$ 处.
记录二：上午 8 时 30 分，渔船到达木兰灯塔 $P$ 北偏西 $45°$ 方向上的 $B$ 处.
记录三：根据气象观测，当天凌晨 4 时到上午 9 时，受天文大潮和天气影响，琼州海峡点 $C$ 周围 5 海里内，会出现异常海况，点 $C$ 位于木兰灯塔 $P$ 北偏东 $15°$ 方向.
请你根据以上信息解决下列问题：
(1) 填空：$\angle PAB =$30$°$，$\angle APC =$75$°$，$AB =$5海里；
(2) 若该渔船不改变航线与速度，是否会进入“海况异常”区？请说明理由.
(参考数据：$\sqrt{2} \approx 1.41$，$\sqrt{3} \approx 1.73$，$\sqrt{6} \approx 2.45$)

答案：
例4　解:
(1)30　75　5
(2)该渔船会进入“海况异常”区.理由:如图，过点P作PD⊥AC，垂足为D.
　　　　
在Rt△BPD中，
∵∠BPD=45°,
∴∠PBD=45°=∠BPD,
∴BD=PD.
在Rt△APD中,
∵∠PAB=30°,tan∠PAD=$\frac{PD}{AD}$,
∴AD=$\sqrt{3}$PD,AP=2PD.
∵AB=AD−BD,
∴5=$\sqrt{3}$PD−PD,
∴PD=BD=$\frac{5\sqrt{3}+5}{2}$海里，
∴AP=2PD=(5$\sqrt{3}$+5)海里.
在△APC中，
∵∠PAB=30°,∠APC=75°,
∴∠PCA=180°−∠PAB−∠APC=75°,
∴∠PCA=∠APC,
∴AC=AP=(5$\sqrt{3}$+5)海里
设上午9时渔船航行至点E处，则AE=10海里，
∴CE=AC−AE=(5$\sqrt{3}$+5)−10=5$\sqrt{3}$−5≈3.65(海里)＜5海里，
∴该渔船会进入“海况异常”区.