《2026年全品中考复习方案数学北师大版》

例4 阅读材料: 整体代值是数学中常用的方法. 例如“已知$3a - b = 2$, 求代数式$6a - 2b - 1$的值.”可以这样解: $6a - 2b - 1 = 2(3a - b) - 1 = 2 × 2 - 1 = 3$. 根据阅读材料, 解决问题: 若$x = 2$是关于$x$的一元一次方程$ax + b = 3$的解, 则代数式$4a^2 + 4ab + b^2 + 4a + 2b - 1$的值是14.

答案： 例4 14

6. (2024 广安) 若$x^2 - 2x - 3 = 0$, 则$2x^2 - 4x + 1 =$7.

答案： 考向精练 6. 7

7. (2024 赤峰) 已知$a^2 - a - 3 = 0$, 求代数式$(a - 2)^2 + (a - 1)(a + 3)$的值.

答案： 考向精练 7. 7

例5 分解因式:
(1)(2025 江西)$a^2 - a =$$a(a - 1)$;
(2)(2025 北京)$7m^2 - 28 =$$7(m + 2)(m - 2)$;
(3)(2025 甘肃)$x^2 - 6x + 9 =$$(x - 3)^{2}$;
(4)(2025 东营)$2m^3 - 12m^2 + 18m =$$2m(m - 3)^{2}$.

答案： 例5
(1)$a(a - 1)$
(2)$7(m + 2)(m - 2)$
(3)$(x - 3)^{2}$
(4)$2m(m - 3)^{2}$

8. (2024 广西) 如果$a + b = 3$, $ab = 1$, 那么$a^3 b + 2a^2 b^2 + ab^3$的值为 (D)

A.0
B.1
C.4
D.9

答案： 考向精练 8. D

9. (2025 自贡) 若$2a + b = -1$, 则$4a^2 + 2ab - b$的值为1.

答案： 考向精练 9. 1

例6 (2024 福建) 已知实数$a$, $b$, $c$, $m$, $n$满足$3m + n = \frac{b}{a}$, $mn = \frac{c}{a}$.
(1) 求证: $b^2 - 12ac$为非负数;
(2) 若$a$, $b$, $c$均为奇数, $m$, $n$是否可以都为整数? 说明你的理由.

答案： 例6 解：
(1) 证明：$\because 3m + n = \frac{b}{a}$，$mn = \frac{c}{a}$，$\therefore b = a(3m + n)$，$c = amn$，则$b^{2} - 12ac = [a(3m + n)]^{2} - 12a^{2}mn$ $= a^{2}(9m^{2} + 6mn + n^{2}) - 12a^{2}mn$ $= a^{2}(9m^{2} - 6mn + n^{2})$ $= a^{2}(3m - n)^{2}$。$\because a$，$m$，$n$均是实数，$\therefore a^{2}(3m - n)^{2} \geq 0$，$\therefore b^{2} - 12ac$为非负数.
(2)$m$，$n$不可以都为整数. 理由如下：若$m$，$n$都为整数，其可能情况有：①$m$，$n$都为奇数；②$m$，$n$为整数，且其中至少有一个为偶数. ①当$m$，$n$都为奇数时，$3m + n$必为偶数. 由
(1)知$b = a(3m + n)$. $\because a$为奇数，$\therefore a(3m + n)$必为偶数，这与$b$为奇数矛盾；②当$m$，$n$为整数，且其中至少有一个为偶数时，$mn$必为偶数. 由
(1)知$c = amn$. $\because a$为奇数，$\therefore amn$必为偶数，这与$c$为奇数矛盾. 综上所述，$m$，$n$不可以都为整数.

10. (2025 浙江) 【文化欣赏】
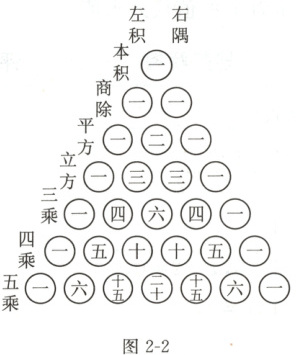
我国南宋时期数学家杨辉于1261年写下《详解九章算法》，书中记载的二项和的乘方$(a+b)^n$展开式的系数规律如图2-2所示，其中“三乘”对应的展开式：
$(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$.
【应用体验】
已知$(x+2)^4=x^4+mx^3+24x^2+32x+16$, 则$m$的值为8.

答案： 考向精练 10. 8