《2025年更高更妙的高中数学思想与方法高中数学选择性必修第一册》

14.在三棱锥$O—ABC$中，$G$是$\triangle ABC$的重心.设$\overrightarrow{OA}=\boldsymbol{a},\overrightarrow{OB}=\boldsymbol{b},\overrightarrow{OC}=\boldsymbol{c}$，以$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$为基向量表示$\overrightarrow{OG}$，则$\overrightarrow{OG}=$$\frac{1}{3}\boldsymbol{a}+\frac{1}{3}\boldsymbol{b}+\frac{1}{3}\boldsymbol{c}$.

答案：
14.$\frac{1}{3}\boldsymbol{a}+\frac{1}{3}\boldsymbol{b}+\frac{1}{3}\boldsymbol{c}$ 解析 如下图所示，连接$AG$并延长交$BC$于点$D$.

所以$\overrightarrow{AG}=2\overrightarrow{GD}$，即$\overrightarrow{OG}-\overrightarrow{OA}=2(\overrightarrow{OD}-\overrightarrow{OG})$所以$\overrightarrow{OG}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OD}$，又$\overrightarrow{OD}=\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$，所以$\overrightarrow{OG}=\frac{1}{3}\boldsymbol{a}+\frac{1}{3}\boldsymbol{b}+\frac{1}{3}\boldsymbol{c}$.

15.已知空间向量$\overrightarrow{PA},\overrightarrow{PB},\overrightarrow{PC}$的模长分别为$1,2,3$，且两两夹角均为$60°$.点$G$为$\triangle ABC$的重心，若$\overrightarrow{PG}=x\overrightarrow{PA}+y\overrightarrow{PB}+z\overrightarrow{PC},x,y,z\in\mathbf{R}$，则$|\overrightarrow{PG}|=$$\frac{5}{3}$.

答案： 15.$\frac{5}{3}$ 解析 因为$G$为$\triangle ABC$的重心，设$BC$中点为$D$，所以$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$，所以$\overrightarrow{PG}-\overrightarrow{PA}=\frac{1}{3}(\overrightarrow{PB}-\overrightarrow{PA}+\overrightarrow{PC}-\overrightarrow{PA})=\frac{1}{3}\overrightarrow{PB}+\frac{1}{3}\overrightarrow{PC}-\frac{2}{3}\overrightarrow{PA}$，所以$\overrightarrow{PG}=\frac{1}{3}\overrightarrow{PA}+\frac{1}{3}\overrightarrow{PB}+\frac{1}{3}\overrightarrow{PC}$，所以$|\overrightarrow{PG}|^{2}=(\frac{1}{3})^{2}×(1^{2}+2^{2}+3^{2}+2× 1× 2× \frac{1}{2}+2× 2× 3× \frac{1}{2})=\frac{25}{9}$，所以$|\overrightarrow{PG}|=\frac{5}{3}$.

16.已知平面单位向量$\boldsymbol{e_1},\boldsymbol{e_2}$满足$\boldsymbol{e_1}·\boldsymbol{e_2}=\frac{1}{2}$，
且$\boldsymbol{a}=x\boldsymbol{e_1}+\boldsymbol{e_2},x\in\mathbf{R},\boldsymbol{b}=2\lambda\boldsymbol{e_1}+(1-\lambda)\boldsymbol{e_2}$，
若使$|\boldsymbol{b}-\boldsymbol{a}|=1$成立的正数$\lambda$有且只有一个，则$x$的取值范围为$\{2\}$.

答案： 16.$\{2\}$ 解析 $\boldsymbol{a}=x\boldsymbol{e_{1}}+\boldsymbol{e_{2}}$，$x\in \mathbf{R}$，$\boldsymbol{b}=2\lambda\boldsymbol{e_{1}}+(1-\lambda)\boldsymbol{e_{2}}$，则$|\boldsymbol{b}-\boldsymbol{a}|=|(2\lambda-x)\boldsymbol{e_{1}}+(1-\lambda-1)\boldsymbol{e_{2}}|=1$，所以$|(2\lambda-x)\boldsymbol{e_{1}}-\lambda\boldsymbol{e_{2}}|^{2}=1$，所以$(2\lambda-x)^{2}-(2\lambda-x)\lambda+\lambda^{2}=1$，故$3\lambda^{2}-3\lambda x+x^{2}-1=0$.
由于使$|\boldsymbol{b}-\boldsymbol{a}|=1$成立的正数$\lambda$有且只有一个，故关于以$\lambda$为未知数的一元二次方程有且只有一个正实数根，故$\Delta=9x^{2}-12(x^{2}-1)=0$，解得$x=\pm 2$，当$x=-2$时，$\lambda＜0$故舍去，则$x=2$.故$x$的范围是唯一一个实数$\{2\}$.

17.如下图所示，已知$M、N$分别为四面体$A—BCD$的面$BCD$与面$ACD$的重心，$G$为$AM$上一点，且$GM:GA=1:3$，设$\overrightarrow{AB}=\boldsymbol{a},\overrightarrow{AC}=\boldsymbol{b},\overrightarrow{AD}=\boldsymbol{c}$，试用$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$表示$\overrightarrow{BG},\overrightarrow{BN}$.

答案： 17.$\overrightarrow{BG}=-\frac{3}{4}\boldsymbol{a}+\frac{1}{4}\boldsymbol{b}+\frac{1}{4}\boldsymbol{c}$，$\overrightarrow{BN}=-\boldsymbol{a}+\frac{1}{3}\boldsymbol{b}+\frac{1}{3}\boldsymbol{c}$ 解析 $\overrightarrow{BG}=\overrightarrow{BM}+\overrightarrow{MG}=\overrightarrow{BM}-\frac{1}{4}\overrightarrow{AM}=\overrightarrow{BM}-\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{BM})=\frac{3}{4}\overrightarrow{BM}-\frac{1}{4}\boldsymbol{a}=\frac{3}{4}× \frac{2}{3}× \frac{1}{2}(\overrightarrow{BC}+\overrightarrow{BD})-\frac{1}{4}\boldsymbol{a}=\frac{1}{4}(\boldsymbol{b}-\boldsymbol{a}+\boldsymbol{c}-\boldsymbol{a})-\frac{1}{4}\boldsymbol{a}=-\frac{3}{4}\boldsymbol{a}+\frac{1}{4}\boldsymbol{b}+\frac{1}{4}\boldsymbol{c}$；
$\overrightarrow{BN}=\overrightarrow{AN}-\overrightarrow{AB}=\frac{2}{3}× \frac{1}{2}(\overrightarrow{AC}+\overrightarrow{AD})-\overrightarrow{AB}=\frac{1}{3}\boldsymbol{b}+\frac{1}{3}\boldsymbol{c}-\boldsymbol{a}$.

18.如下图所示，在三棱锥$A—BCD$中，$E$是$BC$的中点，$F$在$AD$上，且$AF=2FD$，$\overrightarrow{BD}=\boldsymbol{a},\overrightarrow{BC}=\boldsymbol{b},\overrightarrow{BA}=\boldsymbol{c}$.

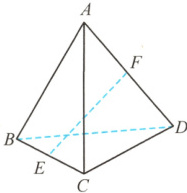
(1)试用$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$表示向量$\overrightarrow{EF}$；
(2)若底面$BCD$是等腰直角三角形，且$BD=BC=AB=3,\angle ABD=\angle ABC=60°$，求$EF$的长.

答案： 18.
(1)$\overrightarrow{EF}=\frac{2}{3}\boldsymbol{a}-\frac{1}{2}\boldsymbol{b}+\frac{1}{3}\boldsymbol{c}$
(2)$|\overrightarrow{EF}|=\frac{\sqrt{31}}{2}$
解析
(1)依题意，因$E$是$BC$的中点，$F$在$AD$上，且$AF = 2FD$，则$\overrightarrow{EF}=\overrightarrow{EB}+\overrightarrow{BA}+\overrightarrow{AF}=\overrightarrow{BA}+\overrightarrow{AF}-\overrightarrow{BE}=\overrightarrow{BA}+\frac{2}{3}\overrightarrow{AD}-\frac{1}{2}\overrightarrow{BC}=\overrightarrow{BA}+\frac{2}{3}(\overrightarrow{BD}-\overrightarrow{BA})-\frac{1}{2}\overrightarrow{BC}=\frac{2}{3}\overrightarrow{BD}-\frac{1}{2}\overrightarrow{BC}+\frac{1}{3}\overrightarrow{BA}=\frac{2}{3}\boldsymbol{a}-\frac{1}{2}\boldsymbol{b}+\frac{1}{3}\boldsymbol{c}$，所以$\overrightarrow{EF}=\frac{2}{3}\boldsymbol{a}-\frac{1}{2}\boldsymbol{b}+\frac{1}{3}\boldsymbol{c}$.
(2)因$BD=BC=AB=3$，$\angle CBD=90^{\circ}$，$\angle ABD=\angle ABC=60^{\circ}$，即$|\boldsymbol{a}|=|\boldsymbol{b}|=|\boldsymbol{c}|=3$，则$\boldsymbol{a}· \boldsymbol{b}=0$，$\boldsymbol{a}· \boldsymbol{c}=\frac{9}{2}$，$\boldsymbol{b}· \boldsymbol{c}=\frac{9}{2}$，由
(1)知：$|\overrightarrow{EF}|=\sqrt{(\frac{2}{3}\boldsymbol{a}-\frac{1}{2}\boldsymbol{b}+\frac{1}{3}\boldsymbol{c})^{2}}=\sqrt{\frac{4}{9}\boldsymbol{a}^{2}+\frac{1}{4}\boldsymbol{b}^{2}+\frac{1}{9}\boldsymbol{c}^{2}-\frac{2}{3}\boldsymbol{a}· \boldsymbol{b}-\frac{1}{3}\boldsymbol{b}· \boldsymbol{c}+\frac{4}{9}\boldsymbol{c}· \boldsymbol{a}}=\frac{\sqrt{31}}{2}$，所以$EF$的长是$\frac{\sqrt{31}}{2}$.

19.已知空间向量$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$两两的夹角均为$60°$，且$|\boldsymbol{a}|=|\boldsymbol{b}|=2,|\boldsymbol{c}|=6$.若向量$\boldsymbol{x},\boldsymbol{y}$分别满足$\boldsymbol{x}·(\boldsymbol{x}+\boldsymbol{a}-\boldsymbol{b})=0$与$\boldsymbol{y}·\boldsymbol{c}-8=0$，则$|\boldsymbol{x}-\boldsymbol{y}|$的最小值是$\frac{1}{3}$.

答案： 19.$\frac{1}{3}$ 解析 由题意$\boldsymbol{a}· \boldsymbol{b}=2× 2× \cos60^{\circ}=2$，$\boldsymbol{a}· \boldsymbol{c}=\boldsymbol{b}· \boldsymbol{c}=2× 6× \cos60^{\circ}=6$.
因为$\boldsymbol{x}· (\boldsymbol{x}+\boldsymbol{a}-\boldsymbol{b})=0$，所以$x^{2}-x· (\boldsymbol{b}-\boldsymbol{a})=(\boldsymbol{x}-\frac{\boldsymbol{b}-\boldsymbol{a}}{2})^{2}-\frac{(\boldsymbol{b}-\boldsymbol{a})^{2}}{4}=0$，$(\boldsymbol{x}-\frac{\boldsymbol{b}-\boldsymbol{a}}{2})^{2}=\frac{\boldsymbol{b}^{2}-2\boldsymbol{a}· \boldsymbol{b}+\boldsymbol{a}^{2}}{4}=1$，所以$|\boldsymbol{x}-\frac{\boldsymbol{b}-\boldsymbol{a}}{2}|=1$，令$\boldsymbol{p}=\frac{\boldsymbol{b}-\boldsymbol{a}}{2}$，则$|\boldsymbol{x}-\boldsymbol{p}|=1$，且$\boldsymbol{p}· \boldsymbol{c}=\frac{\boldsymbol{b}-\boldsymbol{a}}{2}· \boldsymbol{c}=\frac{\boldsymbol{b}· \boldsymbol{c}-\boldsymbol{a}· \boldsymbol{c}}{2}=0$，$|\boldsymbol{x}-\boldsymbol{y}|=|\boldsymbol{x}-\boldsymbol{p}+\boldsymbol{p}-\boldsymbol{y}|\geqslant|\boldsymbol{y}-\boldsymbol{p}|-|\boldsymbol{x}-\boldsymbol{p}|$，由$\boldsymbol{y}· \boldsymbol{c}-8=0$得$8=\boldsymbol{y}· \boldsymbol{c}-\boldsymbol{p}· \boldsymbol{c}=(\boldsymbol{y}-\boldsymbol{p})· \boldsymbol{c}\leqslant |\boldsymbol{y}-\boldsymbol{p}|· |\boldsymbol{c}|$，所以$|\boldsymbol{y}-\boldsymbol{p}|\geqslant \frac{8}{6}=\frac{4}{3}$，所以$|\boldsymbol{x}-\boldsymbol{y}|\geqslant|\boldsymbol{y}-\boldsymbol{p}|-|\boldsymbol{x}-\boldsymbol{p}|\geqslant \frac{4}{3}-1=\frac{1}{3}$，当且仅当$\boldsymbol{p}$,$\boldsymbol{x}$,$\boldsymbol{y}$共线且$\boldsymbol{y}-\boldsymbol{p}$,$\boldsymbol{c}$共线时等号成立.