2025年更高更妙的高中数学思想与方法高中数学选择性必修第一册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年更高更妙的高中数学思想与方法高中数学选择性必修第一册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
变式3 在长方体ABCD−AlBlClD1
中,AB=AA1=2,AD=1,E为CC1的中点,
则异面直线BC1与AE之间的距离是
()
A.$\frac{1}{3}$
B.$\frac{√21}{21}$
C.$\frac{2}{3}$
D.$\frac{2√21}{21}$
中,AB=AA1=2,AD=1,E为CC1的中点,
则异面直线BC1与AE之间的距离是
()
A.$\frac{1}{3}$
B.$\frac{√21}{21}$
C.$\frac{2}{3}$
D.$\frac{2√21}{21}$
答案:
答案 D
解析 由题意建立以A为原点,AB,
AD,AA1为x,y,z轴的空间直角坐标系,如
下图所示:
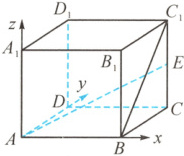
则A(0,0,0),B(2,0,0),
E(2,1,1),C1(2,1,2),
则AE=(2,1,1),BC=(0,1,2).
设n=(x,y,z)使得与BC1、AE均垂直,
n.AE=0,
则{n.BC=0,,得n=($\frac{1}{2}$,−2,1)
则AB在n上的投影为
一
$\frac{n.AB}{n|}$=$\frac{2√21}{21}$,
即异面直线BC1与AE之间的距离
是$\frac{2√21}{21}$.
答案 D
解析 由题意建立以A为原点,AB,
AD,AA1为x,y,z轴的空间直角坐标系,如
下图所示:

则A(0,0,0),B(2,0,0),
E(2,1,1),C1(2,1,2),
则AE=(2,1,1),BC=(0,1,2).
设n=(x,y,z)使得与BC1、AE均垂直,
n.AE=0,
则{n.BC=0,,得n=($\frac{1}{2}$,−2,1)
则AB在n上的投影为
一
$\frac{n.AB}{n|}$=$\frac{2√21}{21}$,
即异面直线BC1与AE之间的距离
是$\frac{2√21}{21}$.
[例4]如下图所示,在四棱锥P一ABCD
中,底面ABCD为直角梯形,AD//BC,AD
⊥CD,BC=$\frac{1}{2}$AD=1且CD=√3,E为AD
的中点,PE⊥底面ABCD,F是棱PA的中
点,PA=2.
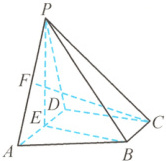
(1)证明:BF//平面PCD;
(2)求平面BDP与平面BDF夹角的余
弦值;
(3)在线段PC(不含端点)上是否存在
点M,使得直线BM和平面BDF所成角的
正弦值为$\frac{√39}{13}$?若存在,求出此时PM的
长;若不存在,说明理由.
中,底面ABCD为直角梯形,AD//BC,AD
⊥CD,BC=$\frac{1}{2}$AD=1且CD=√3,E为AD
的中点,PE⊥底面ABCD,F是棱PA的中
点,PA=2.

(1)证明:BF//平面PCD;
(2)求平面BDP与平面BDF夹角的余
弦值;
(3)在线段PC(不含端点)上是否存在
点M,使得直线BM和平面BDF所成角的
正弦值为$\frac{√39}{13}$?若存在,求出此时PM的
长;若不存在,说明理由.
答案:
答案
(1)略
(2)$\frac{7√65}{65}$
(3)$\frac{√}{3}$
解析
(1)由题意得
BC//DE,BC=DE,∠ADC=90°.
所以四边形BCDE为矩形,又PE⊥平
面ABCD,如下图所示建立空间直角坐标系
E−xyz:

则E(0,0,0),A(1,0,0),B(0,√3,0),
D(−1,0,0),P(0,0,√3),
C(−1,√3,,0),F($\frac{1}{2}$,0,$\frac{√3}{2}$),
DC=(0,√3,0),DP=(1,0,√3).
设平面PCD的法向量为m=(x,y,z),
则{D一DCP..mm==00,,则{√3y=0,
x+√3z=0,
则y=0,不妨设x=一√3,则N=1,
可得m=(−√3,0,1),
又BF=($\frac{1}{2}$,−√3,$\frac{√3}{2}$),可得BF.m=0,
因为直线BFC平面BCD,
所以BF//平面BCD.
(2)设平面PBD的法向量为
n1=(x1,y1,1),
DB=(1,√3,0),BP=(0,−√3,√3),
则{DBPB..nn1==00,,即x−1√+3√y31y+l√=30z,1=0,
{
不妨设x=√3,可得n=(√3,−1,−1),
设平面BDF的法向量为
n2=(x2,y2,22),DF=($\frac{3}{2}$,0,$\frac{√3}{2}$),
DB.n2=0, x2+√3y2=0,
则{DF.n2=0,,即$\frac{3}{2}$x2+$\frac{√3}{2}$x2=0,
{
不妨设x2=√3,可得n2=(−√3,1,3),
平面BDP与平面BDF夹角为α,因此有
cosa=|cos<n,n>|=|$\frac{n.n}{n|.|n|}$|=$\frac{7√65}{65}$,
所以平面BDP与平面BDF夹角的余
弦值为$\frac{7√65}{65}$.
(3)设PM=λPC=λ(−1,√3,−√3)
=(−λ,√3λ,−√3λ),λ∈(0,1)
BM=BP+PM
=(−λ,−√3+√3λ,√3−√3λ),
由
(2)可知平面BDF的法向量为
n2=(−√3,1,3),
一
|cos<BM,n2>|=$\frac{|BM.n}{|BM|.|n|}$
=$\frac{|√3+√3−√3+3√3−3√3|}{√13×√x²+2(√3−√3)²}$=$\frac{√39}{13}$,
则3λ²−4λ+1=0,解得λ=1(舍)或λ=
$\frac{1}{3}$,可得PM=(−$\frac{1}{3}$,$\frac{√3}{3}$,−$\frac{√3}{3}$),
所以|PM|=$\frac{√}{3}$.
点睛 对于存在性问题,我们可以先假
设存在,利用空间向量关系得到一个方程,若
方程有解,则存在,若方程无解,则不存在.
答案
(1)略
(2)$\frac{7√65}{65}$
(3)$\frac{√}{3}$
解析
(1)由题意得
BC//DE,BC=DE,∠ADC=90°.
所以四边形BCDE为矩形,又PE⊥平
面ABCD,如下图所示建立空间直角坐标系
E−xyz:

则E(0,0,0),A(1,0,0),B(0,√3,0),
D(−1,0,0),P(0,0,√3),
C(−1,√3,,0),F($\frac{1}{2}$,0,$\frac{√3}{2}$),
DC=(0,√3,0),DP=(1,0,√3).
设平面PCD的法向量为m=(x,y,z),
则{D一DCP..mm==00,,则{√3y=0,
x+√3z=0,
则y=0,不妨设x=一√3,则N=1,
可得m=(−√3,0,1),
又BF=($\frac{1}{2}$,−√3,$\frac{√3}{2}$),可得BF.m=0,
因为直线BFC平面BCD,
所以BF//平面BCD.
(2)设平面PBD的法向量为
n1=(x1,y1,1),
DB=(1,√3,0),BP=(0,−√3,√3),
则{DBPB..nn1==00,,即x−1√+3√y31y+l√=30z,1=0,
{
不妨设x=√3,可得n=(√3,−1,−1),
设平面BDF的法向量为
n2=(x2,y2,22),DF=($\frac{3}{2}$,0,$\frac{√3}{2}$),
DB.n2=0, x2+√3y2=0,
则{DF.n2=0,,即$\frac{3}{2}$x2+$\frac{√3}{2}$x2=0,
{
不妨设x2=√3,可得n2=(−√3,1,3),
平面BDP与平面BDF夹角为α,因此有
cosa=|cos<n,n>|=|$\frac{n.n}{n|.|n|}$|=$\frac{7√65}{65}$,
所以平面BDP与平面BDF夹角的余
弦值为$\frac{7√65}{65}$.
(3)设PM=λPC=λ(−1,√3,−√3)
=(−λ,√3λ,−√3λ),λ∈(0,1)
BM=BP+PM
=(−λ,−√3+√3λ,√3−√3λ),
由
(2)可知平面BDF的法向量为
n2=(−√3,1,3),
一
|cos<BM,n2>|=$\frac{|BM.n}{|BM|.|n|}$
=$\frac{|√3+√3−√3+3√3−3√3|}{√13×√x²+2(√3−√3)²}$=$\frac{√39}{13}$,
则3λ²−4λ+1=0,解得λ=1(舍)或λ=
$\frac{1}{3}$,可得PM=(−$\frac{1}{3}$,$\frac{√3}{3}$,−$\frac{√3}{3}$),
所以|PM|=$\frac{√}{3}$.
点睛 对于存在性问题,我们可以先假
设存在,利用空间向量关系得到一个方程,若
方程有解,则存在,若方程无解,则不存在.
查看更多完整答案,请扫码查看


