《2025年练习生高中数学选择性必修第二册人教B版》

8. [2022·重庆第八中学高三月考]用黑、白 2 种颜色随机地染如图的 5 个格子，每个格子染 1 种颜色，并且从左到右数，不管数到哪个格子，总有黑色格子不少于白色格子的染色方法种数为 (B)


A.6
B.10
C.16
D.20

答案： 8. B 【解析】依题意，第1个格子必须为黑色，则出现从左到右数，不管数到哪个格子，总有黑色格子不少于白色格子可以分为三类。第一类，全染黑色，有1种方法；第二类，第1个格子染黑色，另外4个格子中有1个格子染白色，剩余的都染黑色，有$\mathrm{C}_{4}^{1}=4$（种）方法；第三类，第1个格子染黑色，另外4个格子中有2个格子染白色（2个染白色的格子不能是第2，3个格子），剩余的都染黑色，有$\mathrm{C}_{4}^{2}-1=5$（种）方法。所以出现从左到右数，不管数到哪个格子，总有黑色格子不少于白色格子的染色方法有$1 + 4 + 5 = 10$（种）。故选B。

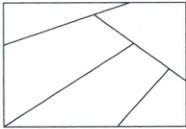
9. (高考快递·原创)在如图的 5 个区域内种植花卉，每个区域种植 1 种花卉，且相邻区域种植的花卉不同. 若有 6 种不同的花卉可供选择，则不同的种植方法种数是 (C)


A.1 440
B.720
C.1 920
D.960

答案：
9. C 【解析】如图，设5个区域分别是A，B，C，D，E。第一步，选择1种花卉种植在B区域，有$\mathrm{C}_{6}^{1}$种花卉可以选择。第二步，从剩下的5种不同的花卉中选择1种种植在A区域，有$\mathrm{C}_{5}^{1}$种花卉可以选择。第三步，从剩下的4种花卉中选择1种种植在C区域，有$\mathrm{C}_{4}^{1}$种花卉可以选择。第四步，选择与B，C不同的花卉种植在D区域，有$\mathrm{C}_{4}^{1}$种花卉可以选择。第五步，选择与B，D不同的花卉种植在E区域，有$\mathrm{C}_{4}^{1}$种花卉可以选择。所以不同的种植方法种数是$6×5×4×4×4 = 1920$。故选C。

10. [2022·河南信阳高二期末]二进制数是用 0 和 1 表示的数，它的基数为 2，进位规则是“逢二进一”，借位规则是“借一当二”. 二进制数 $ (a_{0}a_{1}a_{2}·s a_{k})_{2}(k\in N_{+}) $ 对应的十进制数记为 $ m_{k} $，即 $ m_{k}=a_{0}× 2^{k}+a_{1}× 2^{k - 1}+·s +a_{k - 1}× 2+a_{k}× 2^{0} $，其中 $ a_{0}=1 $，$ a_{i}\in \{ 0,1\} (i = 1,2,3,·s,k) $，则在 $ a_{0} $，$ a_{1} $，$ a_{2} $，$ ·s $，$ a_{8} $ 中恰好有 2 个 0 的所有二进制数 $ (a_{0}a_{1}·s a_{8})_{2} $ 对应的十进制数的和为 (D)

A.1 910
B.1 990
C.12 252
D.12 253

答案： 10. D 【解析】根据题意，得$m_{8}=1×2^{8}+a_{1}×2^{7}+a_{2}×2^{6}+·s+a_{8}×2^{0}$。因为在$a_{0},a_{1},a_{2},·s,a_{8}$中恰好有2个0的有$\mathrm{C}_{8}^{2}=28$（种）可能，即所有符合条件的二进制数$(a_{0}a_{1}a_{2}·s a_{8})_{2}$的个数为28。所以所有二进制数$(a_{0}a_{1}a_{2}·s a_{8})_{2}$对应的十进制数的和中，$2^{8}$出现$\mathrm{C}_{8}^{2}=28$（次），$2^{7},2^{6},·s,2^{1},2^{0}$均出现$\mathrm{C}_{7}^{2}=21$（次），所以满足$a_{0},a_{1},a_{2},·s,a_{8}$中恰好有2个0的所有二进制数$(a_{0}a_{1}a_{2}·s a_{8})_{2}$对应的十进制数的和为$\mathrm{C}_{7}^{2}(2^{7}+2^{6}+·s+2^{1}+2^{0})+\mathrm{C}_{8}^{2}2^{8}=21×255 + 28×256 = 12523$。故选D。

11. 格点是指平面直角坐标系中横、纵坐标均为整数的点. 一格点沿坐标线到原点的最短路程为该点到原点的“格点距离”〔如：若 $ P(-2,1) $，则点 $ P $ 到原点的格点距离为 $ 2 + 1 = 3 $〕. 格点距离为定值的点的轨迹称为“格点圆”，该定值称为格点圆的半径，而每一条最短路径称为一条半径. 当格点半径为 6 时，格点圆的半径有252 条. (用数字作答)

答案：
11. 252 【解析】设格点为$(x,y)$。由格点半径为6，得$|x| + |y| = 6$，所以对应“格点圆”的图像如图，每条边上有（不含端点）5个格点。以第一象限为例，格点有$(1,5)$，$(2,4)$，$(3,3)$，$(4,2)$，$(5,1)$，其中$(1,5)$的半径有6条，$(2,4)$的半径有15条，$(3,3)$的半径有20条，$(4,2)$的半径有15条，$(5,1)$的半径有6条，所以在第一象限的格点圆的半径共有62条。即对于任意格点，其半径有$\mathrm{C}_{|x| + |y|}^{|x|}$条。所以四个象限共有$4×(\mathrm{C}_{6}^{1}+\mathrm{C}_{6}^{2}+\mathrm{C}_{6}^{3}+\mathrm{C}_{6}^{4}+\mathrm{C}_{6}^{5})=248$（条）半径。另外数轴上有$(6,0)$，$(0,6)$，$(-6,0)$，$(0,-6)$共4个点，半径共有$4\mathrm{C}_{6}^{0}=4$（条）。综上可知，格点半径为6时，格点圆的半径有$248 + 4 = 252$（条）。

12. 已知集合 $ M = \{ 0,1,2\} $，函数 $ y = f(x) $ 的定义域为 $ D = \{ 1,2,3,4\} $，值域为 $ A $.
(1)若 $ A = M $，求不同的函数 $ y = f(x) $ 的个数.
(2)若 $ A\subseteq M $，
①求不同的函数 $ y = f(x) $ 的个数；
②若满足 $ f(1)+f(2)+f(3)+f(4)=4 $，求不同的函数 $ y = f(x) $ 的个数.

答案： 12. 【解】
(1)因为函数$f(x)$的定义域是$\{1,2,3,4\}$，值域是$\{0,1,2\}$，所以定义域里有2个数对应着值域里面1个数，另外2个数是1对1，所以不同的函数的个数是$\mathrm{C}_{4}^{2}\mathrm{A}_{3}^{3}=6×6 = 36$。
(2)①对于定义域中的每一个数，都有3种选择，所以共有$3^{4}=81$（个）函数。
②满足$f(1) + f(2) + f(3) + f(4) = 4$的函数可以分三类。
第一类，$f(1)$，$f(2)$，$f(3)$，$f(4)$这4个函数值中有2个对应的是0，有2个对应的是2，则函数的个数是$\frac{\mathrm{C}_{4}^{2}}{\mathrm{A}_{2}^{2}}·\mathrm{A}_{2}^{2}=6$；
第二类，$f(1)$，$f(2)$，$f(3)$，$f(4)$这4个函数值中有1个对应的是0，有2个对应的是1，有1个对应的是2，则函数的个数是$\mathrm{C}_{4}^{2}\mathrm{A}_{2}^{2}=12$；
第三类，$f(1)$，$f(2)$，$f(3)$，$f(4)$这4个函数值对应的都是1，则函数的个数是1。
所以共有$6 + 12 + 1 = 19$（个）函数。