《2025年练习生高中数学选择性必修第二册人教B版》

22. (多选)[2023·江西上饶高二期末]2022 年冬奥会在北京举办，为了弘扬奥林匹克精神，上饶市多所中小学开展了冬奥会项目科普活动. 为了调查学生对冬奥会项目的了解情况，随机抽取了 $ 10 $ 所学校中的部分同学，$ 10 $ 所学校中了解冬奥会项目的人数如图.

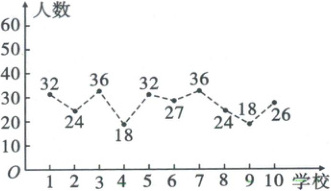
若从这 $ 10 $ 所学校中随机选取 $ 3 $ 所学校进行冬奥会项目的宣讲活动，记 $ X $ 为被选中的学校中了解冬奥会项目的人数在 $ 30 $ 以上的学校数，则下列说法正确的是 (ACD)

A.$ X $ 的可能取值为 $ 0, 1, 2, 3 $
B.$ P(X = 0) = \dfrac{1}{3} $
C.$ E(X) = \dfrac{6}{5} $
D.$ D(X) = \dfrac{14}{25} $

答案： 22. ACD 【解析】由题意可得$X$的可能取值为$0,1,2,3$，故A正确；分析可得$X\sim H(10,3,4)$，则$P(X = 0)=\frac{\mathrm{C}_{4}^{0}\mathrm{C}_{6}^{3}}{\mathrm{C}_{10}^{3}}=\frac{1}{6}$，故B错误；$E(X)=\frac{3×4}{10}=\frac{6}{5}$，故C正确；$D(X)=\frac{6}{5}×\frac{(10 - 4)(10 - 3)}{10×9}=\frac{14}{25}$，故D正确。选ACD。
方法总结 若$X$服从参数为$N,n,M$的超几何分布，即$X\sim H(N,n,M)$，则$E(X)=\frac{nM}{N}$，$D(X)=\frac{nM(N - M)(N - n)}{N^{2}(N - 1)}=E(X)·\frac{(N - M)(N - n)}{N(N - 1)}$。

23. (多选)[2023·河北石家庄高三开学考试]某计算机程序每运行一次都会随机出现一个 $ n $ 位二进制数 $ A = a_1a_2a_3a_4·s a_n $，其中 $ a_i (i = 1, 2, 3, ·s, n) \in \{0, 1\} $. 若在 $ A $ 的各数位上出现 $ 0 $ 和 $ 1 $ 的概率均为 $ \dfrac{1}{2} $，记 $ X = a_1 + a_2 + a_3 + ·s + a_n $，则当程序运行一次时 (ABC)

A.$ P(X = 0) = \dfrac{1}{2^n} $
B.$ P(X = k) = P(X = n - k) (0 \leq k \leq n, k \in \mathbf{N}^*) $
C.$ X $ 的数学期望 $ E(X) = \dfrac{n}{2} $
D.$ X $ 的方差 $ D(X) = \dfrac{n^2}{4} $

答案： 23. ABC 【解析】由二进制数$A$的特点知每一个数位上的数字只能填$0,1$，每位数出现$0,1$是独立的，所以$X\sim B\left(n,\frac{1}{2}\right)$，所以$P(X = 0)=\mathrm{C}_{n}^{0}\left(\frac{1}{2}\right)^{0}\left(1 - \frac{1}{2}\right)^{n}=\frac{1}{2^{n}}$，故A正确；$P(X = k)=\mathrm{C}_{n}^{k}\left(\frac{1}{2}\right)^{k}\left(1 - \frac{1}{2}\right)^{n - k}=\mathrm{C}_{n}^{n - k}\left(\frac{1}{2}\right)^{n - k}\left(1 - \frac{1}{2}\right)^{k}=P(X = n - k)$，$0\leq k\leq n,k\in\mathbf{N}^{*}$，故B正确；因为$X\sim B\left(n,\frac{1}{2}\right)$，所以$E(X)=n×\frac{1}{2}=\frac{n}{2}$，$D(X)=n×\frac{1}{2}×\left(1 - \frac{1}{2}\right)=\frac{n}{4}$，故C正确，D错误。选ABC。

24. [2023·北京高二期末]某地区高中学校期末进行了统一考试，为做好本次考试的评价工作，现随机抽取了 $ 50 $ 名学生的成绩，将其划分为 A，B，C 三个等级. 经统计，这批学生的成绩全部介于 $ 40 $ 分至 $ 100 $ 分之间，将数据按照 $[40, 50)$，$[50, 60)$，$[60, 70)$，$[70, 80)$，$[80, 90)$，$[90, 100]$ 分成 $ 6 $ 组，制成了如图的频率分布直方图.

(1)求频率分布直方图中 $ m $ 的值；
(2)在这 $ 50 $ 名学生中用分层抽样的方法从成绩在 $[70, 80)$，$[80, 90)$，$[90, 100]$ 的三组中抽取 $ 11 $ 人，再从这 $ 11 $ 人中随机抽取 $ 3 $ 人，记 $ \xi $ 为 $ 3 $ 人中成绩在 $[80, 90)$ 的人数，求 $ \xi $ 的分布列和数学期望；
(3)规定成绩在 $[90, 100]$ 的为 A 等级，成绩在 $[70, 90)$ 的为 B 等级，其他为 C 等级. 以样本估计总体，用频率代替概率. 从所有参加考试的同学中随机抽取 $ 3 $ 人，求获得 B 等级的人数不小于 $ 2 $ 的概率.

答案：
24. 【解】
(1)由题意，得$2×0.004×10 + 0.022×10 + 0.03×10 + 0.028×10 + 10m = 1$，
解得$m = 0.012$。
(2)由频率分布直方图，得成绩在$[70,80)$，$[80,90)$，$[90,100]$的三组人数之比为$7:3:1$，
易得分层抽样抽取的成绩在$[70,80)$，$[80,90)$，$[90,100]$的三组人数分别为$7,3,1$（分层抽样的抽样比相同），
得$\xi$的可能取值为$0,1,2,3$[$\xi$服从参数为11，3，3的超几何分布，即$\xi\sim H(11,3,3)$]，
$P(\xi = 0)=\frac{\mathrm{C}_{8}^{3}}{\mathrm{C}_{11}^{3}}=\frac{56}{165}$，$P(\xi = 1)=\frac{\mathrm{C}_{8}^{2}\mathrm{C}_{3}^{1}}{\mathrm{C}_{11}^{3}}=\frac{28}{55}$，$P(\xi = 2)=\frac{\mathrm{C}_{8}^{1}\mathrm{C}_{3}^{2}}{\mathrm{C}_{11}^{3}}=\frac{8}{55}$，$P(\xi = 3)=\frac{\mathrm{C}_{3}^{3}}{\mathrm{C}_{11}^{3}}=\frac{1}{165}$。
所以$\xi$的分布列为

$\therefore E(\xi)=0×\frac{56}{165}+1×\frac{28}{55}+2×\frac{8}{55}+3×\frac{1}{165}=\frac{9}{11}$（也可利用超几何分布的期望公式$E(\xi)=3×\frac{3}{11}=\frac{9}{11}$）。
(3)由题意，成绩为A，B，C等级的频率分别为$0.04,0.4,0.56$。
设从所有参加考试的同学中随机抽取3人，获得B等级的人数为$\eta$，则$\eta\sim B(3,0.4)$，
所以获得B等级的人数不少于2的概率$p=\mathrm{C}_{3}^{2}×0.4^{2}×0.6+\mathrm{C}_{3}^{3}×0.4^{3}=0.352$。