2025年练习生高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
27. [2023·山东烟台招远第一中学高二期中]某人在10次射击中击中目标的次数为$ X $,若 $ X\sim B(10,0.8) $,若 $ P(X = k) $最大,则$ k = $
8
.
答案:
27.8【解析】在10次射击中击中目标的次数$X \sim B(10, 0.8)$,易知$P(X = k) = \mathrm{C}_{10}^{k} · 0.8^{k} · 0.2^{10 - k}$。因为$P(X = k)$最大,所以$\begin{cases} P(X = k) \geq P(X = k + 1) \\ P(X = k) \geq P(X = k - 1) \end{cases}$,即$\begin{cases} \mathrm{C}_{10}^{k} · 0.8^{k} · 0.2^{10 - k} \geq \mathrm{C}_{10}^{k + 1} · 0.8^{k + 1} · 0.2^{9 - k} \\ \mathrm{C}_{10}^{k} · 0.8^{k} · 0.2^{10 - k} \geq \mathrm{C}_{10}^{k - 1} · 0.8^{k - 1} · 0.2^{11 - k} \end{cases}$,即$\begin{cases} k + 1 \geq 4(10 - k) \\ 4(11 - k) \geq k \end{cases}$,解得$\frac{39}{5} \leq k \leq \frac{44}{5}$。因为$k \in \mathrm{N}$且$0 \leq k \leq 10$,所以$k = 8$,即$k = 8$时$P(X = k)$最大。
方法总结:若$P(X = k) = \mathrm{C}_{n}^{k} · p^{k} · (1 - p)^{n - k}$最大,则可得到不等式组$\begin{cases} P(X = k) \geq P(X = k + 1) \\ P(X = k) \geq P(X = k - 1) \end{cases}$,从而求出参数$k$的取值范围,再结合$k$的取值特征,即可得解。
方法总结:若$P(X = k) = \mathrm{C}_{n}^{k} · p^{k} · (1 - p)^{n - k}$最大,则可得到不等式组$\begin{cases} P(X = k) \geq P(X = k + 1) \\ P(X = k) \geq P(X = k - 1) \end{cases}$,从而求出参数$k$的取值范围,再结合$k$的取值特征,即可得解。
28. 已知某排球特色学校的校排球队来自高一、高二、高三年级的学生人数分别为7人、6人、2人.
(1)若从该校队随机抽取3人拍宣传海报,求抽取的3人中恰有1人来自高三年级的概率.
(2)现该校的排球教练对“发球、垫球、扣球”这3个动作技术进行训练,且在训练阶段进行了多轮测试,规定:在一轮测试中,这3个动作至少有2个动作达到“优秀”,则该轮测试记为“优秀”.已知在某一轮测试的3个动作中,甲同学每个动作达到“优秀”的概率均为$ \dfrac{1}{2} $,乙同学每个动作达到“优秀”的概率均为$ \dfrac{2}{3} $,且每名同学的每个动作互不影响,甲、乙两人的测试结果互不影响.记$ X $为甲、乙二人在该轮测试结果为“优秀”的人数,求$ X $的分布列.
(1)若从该校队随机抽取3人拍宣传海报,求抽取的3人中恰有1人来自高三年级的概率.
(2)现该校的排球教练对“发球、垫球、扣球”这3个动作技术进行训练,且在训练阶段进行了多轮测试,规定:在一轮测试中,这3个动作至少有2个动作达到“优秀”,则该轮测试记为“优秀”.已知在某一轮测试的3个动作中,甲同学每个动作达到“优秀”的概率均为$ \dfrac{1}{2} $,乙同学每个动作达到“优秀”的概率均为$ \dfrac{2}{3} $,且每名同学的每个动作互不影响,甲、乙两人的测试结果互不影响.记$ X $为甲、乙二人在该轮测试结果为“优秀”的人数,求$ X $的分布列.
答案:
28.【解】
(1)设事件$A$为“抽取的3人中恰有1人来自高三年级”,则$P(A) = \frac{\mathrm{C}_{13}^{2}\mathrm{C}_{2}^{1}}{\mathrm{C}_{15}^{3}} = \frac{12}{35}$。
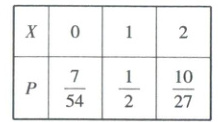
(2)设甲同学在一轮测试中“优秀”动作的个数为$Y$,则有$Y \sim B\left(3, \frac{1}{2}\right)$;设乙同学在一轮测试中“优秀”动作的个数为$Z$,则有$Z \sim B\left(3, \frac{2}{3}\right)$。所以甲同学在一轮测试结果为“优秀”的概率$P(Y \geq 2) = P(Y = 2) + P(Y = 3) = \mathrm{C}_{3}^{2} × \left(\frac{1}{2}\right)^{2} × \left(\frac{1}{2}\right)^{1} + \mathrm{C}_{3}^{3} × \left(\frac{1}{2}\right)^{3} × \left(\frac{1}{2}\right)^{0} = \frac{1}{2}$,乙同学在一轮测试结果为“优秀”的概率$P(Z \geq 2) = P(Z = 2) + P(Z = 3) = \mathrm{C}_{3}^{2} × \left(\frac{2}{3}\right)^{2} × \left(\frac{1}{3}\right)^{1} + \mathrm{C}_{3}^{3} × \left(\frac{2}{3}\right)^{3} × \left(\frac{1}{3}\right)^{0} = \frac{20}{27}$。由题意,得$X$的可能取值为$0, 1, 2$,则$P(X = 0) = \left(1 - \frac{1}{2}\right) × \left(1 - \frac{20}{27}\right) = \frac{7}{54}$,$P(X = 1) = \frac{1}{2} × \left(1 - \frac{20}{27}\right) + \left(1 - \frac{1}{2}\right) × \frac{20}{27} = \frac{1}{2}$,$P(X = 2) = \frac{1}{2} × \frac{20}{27} = \frac{10}{27}$。所以$X$的分布列为
28.【解】
(1)设事件$A$为“抽取的3人中恰有1人来自高三年级”,则$P(A) = \frac{\mathrm{C}_{13}^{2}\mathrm{C}_{2}^{1}}{\mathrm{C}_{15}^{3}} = \frac{12}{35}$。
(2)设甲同学在一轮测试中“优秀”动作的个数为$Y$,则有$Y \sim B\left(3, \frac{1}{2}\right)$;设乙同学在一轮测试中“优秀”动作的个数为$Z$,则有$Z \sim B\left(3, \frac{2}{3}\right)$。所以甲同学在一轮测试结果为“优秀”的概率$P(Y \geq 2) = P(Y = 2) + P(Y = 3) = \mathrm{C}_{3}^{2} × \left(\frac{1}{2}\right)^{2} × \left(\frac{1}{2}\right)^{1} + \mathrm{C}_{3}^{3} × \left(\frac{1}{2}\right)^{3} × \left(\frac{1}{2}\right)^{0} = \frac{1}{2}$,乙同学在一轮测试结果为“优秀”的概率$P(Z \geq 2) = P(Z = 2) + P(Z = 3) = \mathrm{C}_{3}^{2} × \left(\frac{2}{3}\right)^{2} × \left(\frac{1}{3}\right)^{1} + \mathrm{C}_{3}^{3} × \left(\frac{2}{3}\right)^{3} × \left(\frac{1}{3}\right)^{0} = \frac{20}{27}$。由题意,得$X$的可能取值为$0, 1, 2$,则$P(X = 0) = \left(1 - \frac{1}{2}\right) × \left(1 - \frac{20}{27}\right) = \frac{7}{54}$,$P(X = 1) = \frac{1}{2} × \left(1 - \frac{20}{27}\right) + \left(1 - \frac{1}{2}\right) × \frac{20}{27} = \frac{1}{2}$,$P(X = 2) = \frac{1}{2} × \frac{20}{27} = \frac{10}{27}$。所以$X$的分布列为

29. 随着人民生活水平的不断提高,人们对饮食的要求也越来越高.某地区为了解当地餐饮情况,随机抽取了100人对该地区的餐饮情况进行了问卷调查.请根据下面尚未完成的频率分布表和频率分布直方图(如图)解决下列问题.
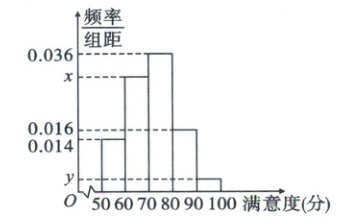
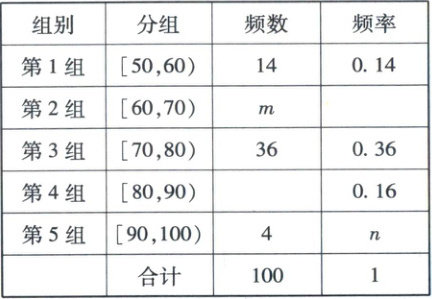
(1)求$ m $,$ n $,$ x $,$ y $的值;
(2)若将满意度不低于80分的人群称为“美食客”,将频率视为概率,用样本估计总体,从该地区中随机抽取3人,记其中“美食客”的人数为$ \xi $,求$ \xi $的分布列.


(1)求$ m $,$ n $,$ x $,$ y $的值;
(2)若将满意度不低于80分的人群称为“美食客”,将频率视为概率,用样本估计总体,从该地区中随机抽取3人,记其中“美食客”的人数为$ \xi $,求$ \xi $的分布列.
答案:
29.【解】
(1)由题意可得第4组的人数为$100 × 0.16 = 16$,所以$m = 100 - 14 - 36 - 16 - 4 = 30$,$n = \frac{4}{100} = 0.04$。又$[60, 70)$内的频率为$\frac{30}{100} = 0.3$,所以$x = \frac{0.3}{10} = 0.03$,$[90, 100)$内的频率为$0.04$,所以$y = \frac{0.04}{10} = 0.004$。
(2)由频率分布表可得在该地区抽到“美食客”的概率为$0.16 + 0.04 = 0.2$。由题意$\xi$可取$0, 1, 2, 3$,且$\xi \sim B\left(3, \frac{1}{5}\right)$,所以$P(\xi = 0) = \mathrm{C}_{3}^{0} × \left(\frac{1}{5}\right)^{0} × \left(\frac{4}{5}\right)^{3} = \frac{64}{125}$,$P(\xi = 1) = \mathrm{C}_{3}^{1} × \left(\frac{1}{5}\right)^{1} × \left(\frac{4}{5}\right)^{2} = \frac{48}{125}$,$P(\xi = 2) = \mathrm{C}_{3}^{2} × \left(\frac{1}{5}\right)^{2} × \left(\frac{4}{5}\right)^{1} = \frac{12}{125}$,$P(\xi = 3) = \mathrm{C}_{3}^{3} × \left(\frac{1}{5}\right)^{3} × \left(\frac{4}{5}\right)^{0} = \frac{1}{125}$,所以$\xi$的分布列为
| $\xi$ | $0$ | $1$ | $2$ | $3$ |
| --- | --- | --- | --- | --- |
| $P$ | $\frac{64}{125}$ | $\frac{48}{125}$ | $\frac{12}{125}$ | $\frac{1}{125}$ |
(1)由题意可得第4组的人数为$100 × 0.16 = 16$,所以$m = 100 - 14 - 36 - 16 - 4 = 30$,$n = \frac{4}{100} = 0.04$。又$[60, 70)$内的频率为$\frac{30}{100} = 0.3$,所以$x = \frac{0.3}{10} = 0.03$,$[90, 100)$内的频率为$0.04$,所以$y = \frac{0.04}{10} = 0.004$。
(2)由频率分布表可得在该地区抽到“美食客”的概率为$0.16 + 0.04 = 0.2$。由题意$\xi$可取$0, 1, 2, 3$,且$\xi \sim B\left(3, \frac{1}{5}\right)$,所以$P(\xi = 0) = \mathrm{C}_{3}^{0} × \left(\frac{1}{5}\right)^{0} × \left(\frac{4}{5}\right)^{3} = \frac{64}{125}$,$P(\xi = 1) = \mathrm{C}_{3}^{1} × \left(\frac{1}{5}\right)^{1} × \left(\frac{4}{5}\right)^{2} = \frac{48}{125}$,$P(\xi = 2) = \mathrm{C}_{3}^{2} × \left(\frac{1}{5}\right)^{2} × \left(\frac{4}{5}\right)^{1} = \frac{12}{125}$,$P(\xi = 3) = \mathrm{C}_{3}^{3} × \left(\frac{1}{5}\right)^{3} × \left(\frac{4}{5}\right)^{0} = \frac{1}{125}$,所以$\xi$的分布列为
| $\xi$ | $0$ | $1$ | $2$ | $3$ |
| --- | --- | --- | --- | --- |
| $P$ | $\frac{64}{125}$ | $\frac{48}{125}$ | $\frac{12}{125}$ | $\frac{1}{125}$ |
查看更多完整答案,请扫码查看


