《2025年练习生高中数学选择性必修第二册人教B版》

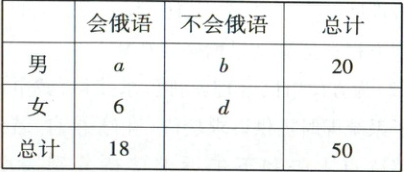
1. 博鳌亚洲论坛 2018 年年会于 4 月 8 日至 11 日在海南博鳌举行. 为了搞好对外宣传工作，会务组选聘了 50 名记者担任对外翻译工作，在“性别与是否会俄语”的 $2×2$ 列联表中，$a - b + d=$28.

答案： 1. 28 【解析】由$2×2$列联表，得$a + 6 = 18$，所以$a = 12$。因为$a + b = 20$，所以$b = 8$。因为$6 + d = 30$，所以$d = 24$，所以$a - b + d = 12 - 8 + 24 = 28$。

2. [2023·陕西咸阳高二期中]某校 160 名男生中有 90 名近视，150 名女生中有 75 名近视，在检验这些学生眼睛近视是否与性别有关时，用什么方法最有说服力(D)

A.平均数
B.方差
C.回归分析
D.独立性检验

答案： 2. D 【解析】是否近视与性别是两类变量，在检验两个随机事件是否相关时，最有说服力的方法是独立性检验（独立性检验用于检验两个随机事件是否相关）。故选 D。

3. 下列关于回归分析与独立性检验的说法正确的是(C)

A.回归分析和独立性检验没有什么区别
B.回归分析是对两个变量准确关系的分析，而独立性检验是分析两个变量之间的不确定性关系
C.回归分析研究两个变量之间的相关关系，独立性检验是对两个变量是否具有某种关系的一种检验
D.独立性检验可以 $100\%$ 确定两个变量之间是否具有某种关系

答案： 3. C 【解析】回归分析是对两个变量之间的相关关系的一种分析，而相关关系是一种不确定关系，通过回归分析预测和估计两个变量之间具有的相关关系；独立性检验是对两个变量之间是否具有某种关系的分析，并且可以分析这两个变量在多大程度上具有这种关系，但不能$100\%$肯定这种关系。故 ABD 错误，C 正确。选 C。

4. (多选)[2023·河南南阳高二期中]某机构为了调查某地中学生是否喜欢数学课与性别之间的关系，通过抽样调查的方式收集数据，经过计算得到 $\chi^{2}=5.805$，由 $P(\chi^{2}\geq3.841)=0.05$，可知下列结论正确的是(BD)

A.有 $95\%$ 的把握认为该地中学生是否喜欢数学课与性别无关
B.有 $95\%$ 的把握认为该地中学生是否喜欢数学课与性别有关
C.在犯错误的概率不超过 $5\%$ 的前提下，可以认为该地中学生是否喜欢数学课与性别无关
D.在犯错误的概率不超过 $5\%$ 的前提下，可以认为该地中学生是否喜欢数学课与性别有关

答案： 4. BD 【解析】因为$\chi^{2}=5.805 ＞ 3.841$（需判断$\chi^{2}=5.805$与$3.841$的关系，当大于$3.841$时，才能有$95\%$的把握认为二者有关），所以有$95\%$的把握认为该地中学生是否喜欢数学课与性别有关，即在犯错误的概率不超过$5\%$的前提下，可以认为该地中学生是否喜欢数学课与性别有关。故选 BD。
方法总结 独立性检验的具体做法
(1) 根据实际问题的需要确定允许推断“变量$X$与$Y$有关系”犯错误的概率的上界$\alpha$，然后查表确定临界值$k$。
(2) 利用公式$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$计算统计量$\chi^{2}$。
(3) 如果$\chi^{2}\geq k$，“$X$与$Y$有关系”这种推断犯错误的概率不超过$\alpha$；否则，就认为在犯错误的概率不超过$\alpha$的前提下不能推断“$X$与$Y$有关系”，或者在样本数据中没有发现足够的证据支持结论“$X$与$Y$有关系”。

5. (多选)[2023·湖北武汉高三期中]为比较甲、乙两所学校学生的数学水平，采用简单随机抽样的方法抽取 88 名学生，为判断学生数学成绩是否优秀与学校之间的关系，统计得到了如下 $2×2$ 列联表.

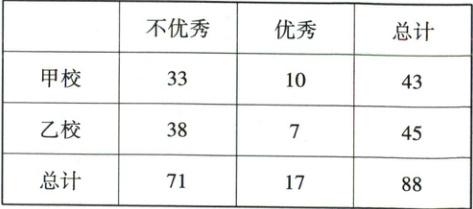
则下列说法正确的是(ACD)

A.根据小概率 $\alpha = 0.1$ 的独立性检验，学生数学成绩是否优秀与在哪所学校无关
B.根据小概率 $\alpha = 0.1$ 的独立性检验，学生数学成绩是否优秀与在哪所学校有关，该推断犯错误的概率不超过 $0.1$
C.若将表中所有数据都扩大为原来的 $10$ 倍，根据小概率 $\alpha = 0.1$ 的独立性检验，学生数学成绩是否优秀与在哪所学校有关，该推断犯错误的概率不超过 $0.1$
D.若将表中所有数据都扩大为原来的 $10$ 倍，根据小概率 $\alpha = 0.001$ 的独立性检验，学生数学成绩是否优秀与在哪所学校无关

答案： 5. ACD 【解析】由题意可知$\chi^{2}=\frac{88×(33×7 - 10×38)^{2}}{43×45×71×17}\approx0.837 ＜ 2.706$（当题干没有给出数据保留小数点位数时，一般至少保留题干所给数据的小数点位数），所以根据小概率$\alpha = 0.1$的独立性检验，学生数学成绩是否优秀与在哪所学校无关，选项 A 正确，选项 B 错误。若将表中所有数据都扩大为原来的$10$倍，则$\chi^{2}=\frac{880×(330×70 - 100×380)^{2}}{430×450×710×170}\approx8.365 ＞ 7.879$（当数据都扩大为原来的$10$倍时，$\chi^{2}$也相应扩大$10$倍），所以根据小概率$\alpha = 0.1$的独立性检验，学生数学成绩是否优秀与在哪所学校有关，该推断犯错误的概率不超过$0.1$，选项 C 正确。若将表中所有数据都扩大为原来的$10$倍，则$\chi^{2}=\frac{880×(330×70 - 100×380)^{2}}{430×450×710×170}\approx8.365 ＜ 10.828$，所以根据小概率$\alpha = 0.001$的独立性检验，学生数学成绩是否优秀与在哪所学校无关，选项 D 正确，故选 ACD。