2025年练习生高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6. (多选)[2023·云南红河高三一模]某校高三一名数学教师从该校高三学生中随机抽取男、女生各 50 名进行了身高统计,得到男、女身高分别近似服从参数为 $173$,$11$ 的正态分布和参数为 $164$,$9$ 的正态分布,并对其是否喜欢体育锻炼进行数据统计,得到如下 $2×2$ 列联表.
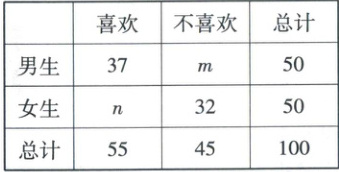
则下列说法正确的是(
A.$m = 13$,$n = 18$
B.男生身高的平均数约为 $173$,女生身高的平均数约为 $164$
C.男生身高的标准差约为 $11$,女生身高的标准差约为 $9$
D.依据 $\alpha = 0.01$ 的独立性检验,认为喜欢体育锻炼与性别有关联

则下列说法正确的是(
ABCD
)A.$m = 13$,$n = 18$
B.男生身高的平均数约为 $173$,女生身高的平均数约为 $164$
C.男生身高的标准差约为 $11$,女生身高的标准差约为 $9$
D.依据 $\alpha = 0.01$ 的独立性检验,认为喜欢体育锻炼与性别有关联
答案:
6. ABCD 【解析】对于 A,因为$37 + m = 50$,$n + 32 = 50$,所以$m = 13$,$n = 18$,A 正确。对于 B,在正态分布$N(\mu,\sigma^{2})$中,$\mu$为平均数,所以男生身高的平均数约为$173$,女生身高的平均数约为$164$,B 正确。对于 C,在服从参数为$\mu$与$\sigma$的正态分布中,$\sigma^{2}$为方差,$\sigma$为标准差,男生身高的标准差约为$11$,女生身高的标准差约为$9$,C 正确。对于 D,$\chi^{2}=\frac{100×(37×32 - 13×18)^{2}}{50×50×55×45}=14.586 > 6.635$,依据$\alpha = 0.01$的独立性检验,认为喜欢体育锻炼与性别有关联,D 正确。故选 ABCD。
7. [2023·上海崇明中学高三模拟]在对吸烟与患肺病这两个分类变量的独立性检验中,下列说法正确的是(
①若 $\chi^{2}$ 的观测值满足 $\chi^{2}\geq6.635$,则我们有 $99\%$ 的把握认为吸烟与患肺病有关系;
②若 $\chi^{2}$ 的观测值满足 $\chi^{2}\geq6.635$,则在 $100$ 个吸烟的人中约有 $99$ 人患有肺病;
③从独立性检验可知,如果有 $99\%$ 的把握认为吸烟与患肺病有关系,那么我们就认为每个吸烟的人有 $99\%$ 的可能性会患肺病;
④从统计量中得知有 $99\%$ 的把握认为吸烟与患肺病有关系,是指有 $1\%$ 的可能性使推断出现错误.
A.①
B.①④
C.②③
D.①②③④
B
)①若 $\chi^{2}$ 的观测值满足 $\chi^{2}\geq6.635$,则我们有 $99\%$ 的把握认为吸烟与患肺病有关系;
②若 $\chi^{2}$ 的观测值满足 $\chi^{2}\geq6.635$,则在 $100$ 个吸烟的人中约有 $99$ 人患有肺病;
③从独立性检验可知,如果有 $99\%$ 的把握认为吸烟与患肺病有关系,那么我们就认为每个吸烟的人有 $99\%$ 的可能性会患肺病;
④从统计量中得知有 $99\%$ 的把握认为吸烟与患肺病有关系,是指有 $1\%$ 的可能性使推断出现错误.
A.①
B.①④
C.②③
D.①②③④
答案:
7. B 【解析】若$\chi^{2}$的观测值满足$\chi^{2}\geq6.635$,则我们有$99\%$的把握认为吸烟与患肺病有关系,而得知有$99\%$的把握认为吸烟与患肺病有关系时,仍有$1\%$的可能性使推断出现错误,但不能说明在$100$个吸烟的人中约有$99$人患有肺病,及每个吸烟的人有$99\%$的可能性会患肺病。故①④正确,②③错误。选 B。
易错规避 当$\chi^{2}\geq k_{0}$时,有$P(\chi^{2}\geq k_{0})$的把握说变量$X$,$Y$有关系,或者说在犯错误的概率不超过$1 - P(\chi^{2}\geq k_{0})$的前提下认为变量$X$,$Y$有关系。若$\chi^{2}\geq6.635$,只能说明,有$99\%$的把握认为吸烟与患肺病有关,但不能说明$100$个吸烟中约$99$人患肺病,也不能说明吸烟的人有$99\%$的可能患肺病。
易错规避 当$\chi^{2}\geq k_{0}$时,有$P(\chi^{2}\geq k_{0})$的把握说变量$X$,$Y$有关系,或者说在犯错误的概率不超过$1 - P(\chi^{2}\geq k_{0})$的前提下认为变量$X$,$Y$有关系。若$\chi^{2}\geq6.635$,只能说明,有$99\%$的把握认为吸烟与患肺病有关,但不能说明$100$个吸烟中约$99$人患肺病,也不能说明吸烟的人有$99\%$的可能患肺病。
8. [2023·河南南阳高二期中]已知两个分类变量 $X$,$Y$ 的可能取值分别为 $\{x_{1},x_{2}\}$ 和 $\{y_{1},y_{2}\}$,通过随机调查得到样本数据,再整理成如下的 $2×2$ 列联表,其中 $a < b$,当判断 $X$ 与 $Y$ 有关系的把握最小时,$a$ 的值为(

A.$5$
B.$10$
C.$15$
D.$17$
C
)
A.$5$
B.$10$
C.$15$
D.$17$
答案:
8. C 【解析】在两个分类变量的列联表中,当$\vert ad - bc\vert$的值越小时,两个分类变量有关的可能性越小。令$\vert ad - bc\vert = 0$,得$ab = 10×30 = 300$。$\because$样本容量为$75$,$\therefore a + b + 40 = 75$,则$b = 35 - a$,$\therefore ab = a(35 - a)=300$,化简得$a^{2}-35a + 300 = 0$,解得$a_{1}=15$,$a_{2}=20$。又$\because a < b$,$\therefore a = 15$。故选 C。
9. [2023·上海杨浦高级中学高三开学考试]北京冬奥会的举办掀起了一阵冰雪运动的热潮. 某高校在本校学生中对“喜欢滑冰是否与性别有关”做了一次调查,参与调查的学生中,男生人数是女生人数的 $3$ 倍,有 $\frac{2}{3}$ 的男生喜欢滑冰,有 $\frac{1}{3}$ 的女生喜欢滑冰. 若根据独立性检验的方法,有 $95\%$ 的把握认为是否喜欢滑冰和性别有关,则参与调查的男生人数可能为(
A.$12$
B.$18$
C.$36$
D.$48$
C
)A.$12$
B.$18$
C.$36$
D.$48$
答案:
9. C 思维路径 设男生人数为$3x$→女生人数为$x$→写出列联表→根据卡方计算公式确定$x$的取值范围→确定男生可能人数。
【解析】设男生人数为$3x$,则女生人数为$x$(当只知道比例关系,不知具体数据时,设参数,最后都会消掉),且$x\in\mathbf{N}_{+}$,可得$2×2$列联表如下:
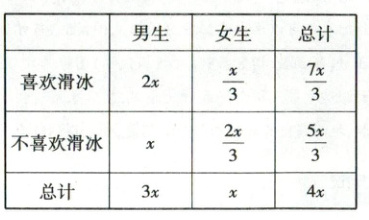
所以$\chi^{2}=\frac{4x\left(2x·\frac{2x}{3}-\frac{x}{3}· x\right)^{2}}{\frac{7x}{3}·\frac{5x}{3}·3x· x}=\frac{12x}{35}$。因为有$95\%$的把握认为是否喜欢滑冰和性别有关,所以$\frac{12x}{35}\in[3.841,5.024)$,解得$11.20\leq x < 14.65$,所以$33.60\leq3x < 43.95$,结合选项只有$36\in[33.60,43.95)$。故选 C。
9. C 思维路径 设男生人数为$3x$→女生人数为$x$→写出列联表→根据卡方计算公式确定$x$的取值范围→确定男生可能人数。
【解析】设男生人数为$3x$,则女生人数为$x$(当只知道比例关系,不知具体数据时,设参数,最后都会消掉),且$x\in\mathbf{N}_{+}$,可得$2×2$列联表如下:

所以$\chi^{2}=\frac{4x\left(2x·\frac{2x}{3}-\frac{x}{3}· x\right)^{2}}{\frac{7x}{3}·\frac{5x}{3}·3x· x}=\frac{12x}{35}$。因为有$95\%$的把握认为是否喜欢滑冰和性别有关,所以$\frac{12x}{35}\in[3.841,5.024)$,解得$11.20\leq x < 14.65$,所以$33.60\leq3x < 43.95$,结合选项只有$36\in[33.60,43.95)$。故选 C。
10. [2023·江西景德镇一中高二期中]为了判断某高中学生选科与性别的关系,现随机抽取 $50$ 名学生,得到如下的 $2×2$ 列联表. 已知 $P(\chi^{2}\geq3.841)\approx0.05$,$P(\chi^{2}\geq6.635)\approx0.01$,则认为选科与性别有关系出错的概率约为
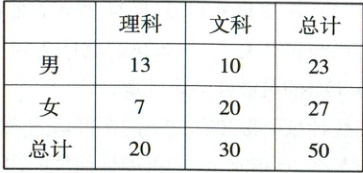
0.05
.
答案:
10. 0.05 【解析】因为$\chi^{2}=\frac{50×(13×20 - 10×7)^{2}}{20×30×23×27}\approx4.844$,且$P(\chi^{2}\geq3.841)\approx0.05$,所以认为选科与性别有关系出错的概率约为$0.05$。
查看更多完整答案,请扫码查看


