《2025年练习生高中数学选择性必修第二册人教B版》

8. [2023·陕西西安高二阶段练习]已知某个样本中的变量$x,y$线性相关，相关系数$r＜0$，则在以$(\overline{x},\overline{y})$为坐标原点的坐标系下的散点图中，大多数的点都落在第二、四象限。

答案： 8. 二、四 【解析】由$r ＜ 0 $，得变量$x, y $呈负相关关系。所以变量$x, y $间的线性回归方程$\hat{y} = \hat{b}x + \hat{a} $中的$\hat{b} ＜ 0 $。又$(\bar{x}, \bar{y}) $为坐标原点，故大多数的点都落在第二、四象限。

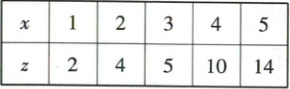
9. [2023·江西九江高三二模]已知变量的关系可以用模型$y=ke^{mx}$拟合，设$z=\ln y$，其变换后得到一组数据(如表)。由表可得线性回归方程$z = 3x + a$，则$k=$(B)


A.$e^{-3}$
B.$e^{-2}$
C.$e^{2}$
D.$e^{3}$

答案： 9. B 思路路径 根据点$(\bar{x}, \bar{z}) $满足线性回归方程$ \to \hat{a} = -2 \to $利用对数运算法则即可得$\ln k + mx = 3x - 2 \to k = e^{-2} $。
【解析】由表格数据知$\bar{x} = 3 $，$\bar{z} = 7 $。将其代入$z = 3x + a $，得$a = 7 - 3 × 3 = -2 $，即$z = 3x - 2 $，所以$z = \ln y = \ln k + mx = 3x - 2 $，即$\ln k = -2 $，可得$k = e^{-2} $。故选B。

10. [2023·重庆高三二模]用模型$y=ae^{kx}$拟合一组数据$(x_{i},y_{i})(i = 1,2,·s,7)$，其中$x_{1}+x_{2}+·s+x_{7}=7$，设$z=\ln y$，得变换后的线性回归方程为$\hat{z}=x + 4$，则$y_{1}y_{2}·s y_{7}=$(C)

A.$e^{70}$
B.$70$
C.$e^{35}$
D.$35$

答案： 10. C 【解析】因为$x_1 + x_2 + ·s + x_7 = 7 $，所以$\bar{x} = 1 $，$\bar{z} = \bar{x} + 4 = 5 $，即$\frac{\ln y_1 + \ln y_2 + ·s + \ln y_7}{7} = \frac{\ln (y_1 y_2 ·s y_7)}{7} = 5 $，所以$y_1 y_2 ·s y_7 = e^{35} $。故选C。

11. [2023·上海建平中学高三开学考试]已知具有相关关系的两个随机变量的一组观测数据的散点图分布在函数$y = 3e^{2x + 1}$的图像附近，则可通过转换得到的线性回归方程为u = 2x + ln3 + 1。

答案： 11. $u = 2x + \ln 3 + 1 $ 【解析】由$y = 3e^{2x + 1} $，得$\ln y = \ln (3e^{2x + 1}) $，即$\ln y = 2x + \ln 3 + 1 $。令$u = \ln y $，则线性回归方程为$u = 2x + \ln 3 + 1 $。

12. [2023·北京第一六六中学高二阶段练习]在研究急刹车的停车距离问题时，通常假定停车距离等于反应距离$d_{1}$(单位：$m$)与制动距离$d_{2}$(单位：$m$)之和。如图为某实验所测得的数据，其中“$KPH$”表示刹车时汽车的初速度$v$(单位：$km/h$)。根据实验数据可以推测，下面四组函数最适合描述$d_{1},d_{2}$与$v$的关系的是(B)


A.$d_{1}=\alpha v,d_{2}=\beta\sqrt{v}$
B.$d_{1}=\alpha v,d_{2}=\beta v^{2}$
C.$d_{1}=\alpha\sqrt{v},d_{2}=\beta v$
D.$d_{1}=\alpha\sqrt{v},d_{2}=\beta v^{2}$

答案：
12. B 【解析】设$d_1(v) = f(v) $，$d_2(v) = g(v) $。由题图知，$d_1(v) = f(v) $过点$(40, 8.5) $，$(50, 10.3) $，$(60, 12.5) $，$(70, 14.6) $，$(80, 16.7) $，$(90, 18.7) $，$(100, 20.8) $，$(110, 22.9) $，$(120, 25) $，$(130, 27.1) $，$(140, 29.2) $，$(150, 31.3) $，$(160, 33.3) $，$(170, 35.4) $，$(180, 37.5) $。作出散点图，如图
(1)。

由图
(1)可得，$d_1 $与$v $呈现线性关系，可选择用$d_1 = \alpha v $。$d_2(v) = g(v) $过点$(40, 8.5) $，$(50, 16.2) $，$(60, 23.2) $，$(70, 31.4) $，$(80, 35.6) $，$(90, 52) $，$(100, 64.6) $，$(110, 78.1) $，$(120, 93) $，$(130, 108.5) $，$(140, 123) $，$(150, 144.1) $，$(160, 164.3) $，$(170, 183.6) $，$(180, 208) $。
作出散点图，如图
(2)。

由图
(2)可得，$d_2 $与$v $呈现非线性关系，结合函数图像的性质，可选择用函数$d_2 = \beta v^2 $。故选B。
易错规避 根据散点图判断回归模型，当其大致成一条直线时，为线性关系；当其增长速度很快时，一般为指数关系；当其增长速度较慢时，一般为对数关系。

13. [2023·浙江杭州高三模拟]某兴趣小组研究光照时长$x$(单位：$h$)和向日葵种子发芽数量$y$(单位：颗)之间的关系，采集$5$组数据，作出如图的散点图。若去掉$D(10,2)$后，下列说法正确的是(D)


A.相关系数$r$变小
B.相关系数$r＜0$
C.残差平方和变大
D.$x$与$y$的相关性变强

答案： 13. D 【解析】从图中可以看出$D(10, 2) $较其他点，偏离直线较远，故去掉$D(10, 2) $后，拟合效果更好。对于A，相关系数$|r| $越接近于1，相关性越强，若去掉$D(10, 2) $后，相关系数$r $变大，故A错误；对于B，由图可知，$y $与$x $成正线性相关关系，故$r ＞ 0 $，B错误；对于C，残差平方和越小，模型的拟合效果越好，若去掉$D(10, 2) $后，则残差平方和变小，故C错误；对于D，若去掉$D(10, 2) $后，$x $与$y $的相关性变强，且是正相关，故D正确。选D。

14. [2023·云南昆明一中高三阶段练习]小王新开了一家小型餐馆，该店第一周的营业净收入数据(单位：元)统计如下：

其中第$4$天和第$6$天的数据由于某种原因造成模糊，但知道$7$天的营业净收入平均值是$23$。已知营业净收入$y$与天数$x$可以用回归直线方程$\hat{y}=\hat{b}x+\hat{a}$拟合，且第$7$天的残差是$-0.6$，则$\hat{a}+\hat{b}$的值是(A)

A.$10.4$
B.$6.2$
C.$4.2$
D.$2$

答案： 14. A 【解析】由残差$e_i = y_i - \hat{y}_i $得$ -0.6 = 35 - \hat{y}_7 $，即$\hat{y}_7 = 35.6 $，所以$35.6 = 7\hat{b} + \hat{a} $①。因为回归直线$\hat{y} = \hat{b}x + \hat{a} $经过点$(\bar{x}, \bar{y}) $（利用回归直线方程过样本的中心点，求参数），且$\bar{x} = 4 $，$\bar{y} = 23 $，所以$23 = 4\hat{b} + \hat{a} $②，联立①②解得$\hat{a} = 6.2 $，$\hat{b} = 4.2 $，所以$\hat{a} + \hat{b} = 10.4 $。故选A。