2025年练习生高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. [2023·山西朔州怀仁第一中学高二期中]若随机变量 η 的分布列如下表,则 $ P(η≤1) = $(

A.0.5
B.0.2
C.0.4
D.0.3
C
)
A.0.5
B.0.2
C.0.4
D.0.3
答案:
1. C 【解析】由分布列可得$P(\eta \leq 1)=P(\eta = -1)+P(\eta = 0)+P(\eta = 1)=0.1 + 0.1 + 0.2 = 0.4$。故选 C。
2. [2022·辽宁辽阳高二期末]甲、乙两名篮球运动员每次投篮的命中率分别为 0.8,0.7,他们各自投篮 1 次,设两人命中总次数为 $ X $,则 $ X $ 的分布列为(
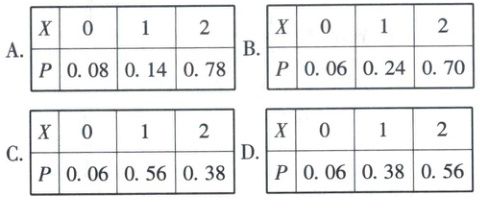
D
)
答案:
2. D 【解析】易知$X$的可能取值为$0,1,2$,$P(X = 0)=0.2 × 0.3 = 0.06$,$P(X = 1)=0.8 × 0.3 + 0.2 × 0.7 = 0.38$,$P(X = 2)=0.8 × 0.7 = 0.56$,故$X$的分布列为
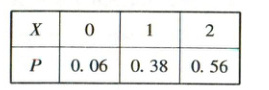
故选 D。
2. D 【解析】易知$X$的可能取值为$0,1,2$,$P(X = 0)=0.2 × 0.3 = 0.06$,$P(X = 1)=0.8 × 0.3 + 0.2 × 0.7 = 0.38$,$P(X = 2)=0.8 × 0.7 = 0.56$,故$X$的分布列为

故选 D。
3. [2023·陕西宝鸡高二期末]已知随机变量 $ X $ 的分布列如下表,若 $ Y = 2X + 1 $,则 $ P(Y = 3) $ 的值为(
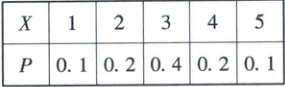
A.0.1
B.0.2
C.0.3
D.0.4
A
)
A.0.1
B.0.2
C.0.3
D.0.4
答案:
3. A 【解析】因为$Y = 2X + 1$,所以当$Y = 3$时,$X = 1$,所以$P(Y = 3)=P(X = 1)=0.1$。故选 A。
4. [2023·浙江杭州四中高二期中]若随机变量 $ X $ 的分布列为 $ P(X = k) = \frac{c}{k(1 + k)} $, $ k = 1,2,3 $,其中 $ c $ 为常数,则 $ P(X≥2) $ 等于(
A.$ \frac{1}{3} $
B.$ \frac{2}{3} $
C.$ \frac{2}{9} $
D.$ \frac{8}{9} $
A
)A.$ \frac{1}{3} $
B.$ \frac{2}{3} $
C.$ \frac{2}{9} $
D.$ \frac{8}{9} $
答案:
4. A 【解析】$P(X = 1)+P(X = 2)+P(X = 3)=\frac{c}{2}+\frac{c}{6}+\frac{c}{12}=1$,解得$c = \frac{4}{3}$,所以$P(X \geq 2)=P(X = 2)+P(X = 3)=\frac{c}{6}+\frac{c}{12}=\frac{1}{4}c = \frac{1}{3}$。故选 A。
5. [2023·辽宁辽河油田第二高级中学高二期末]若离散型随机变量 $ X $ 的分布列如下表,则常数 $ a $ 的值为(

A.$ \frac{1}{3} $
B.$ \frac{2}{3} $
C.$ \frac{2}{3} $ 或 $ \frac{1}{3} $
D.1 或 $ \frac{1}{3} $
A
)
A.$ \frac{1}{3} $
B.$ \frac{2}{3} $
C.$ \frac{2}{3} $ 或 $ \frac{1}{3} $
D.1 或 $ \frac{1}{3} $
答案:
5. A 【解析】由随机变量的分布列的性质知,$\begin{cases}0 \leq 6a^2 - a \leq 1, \\ 0 \leq 3 - 7a \leq 1, \\ 6a^2 - a + 3 - 7a = 1\end{cases}$(注意保证概率非负),$\therefore a = \frac{1}{3}$。故选 A。
方法总结 离散型随机变量的分布列的概率之和为$1$,且各个概率的范围为$[0,1]$。在解题时,一定要注意各个概率加起来是否为$1$,以验证分布列是否求解正确;求参数时,要注意概率非负。
方法总结 离散型随机变量的分布列的概率之和为$1$,且各个概率的范围为$[0,1]$。在解题时,一定要注意各个概率加起来是否为$1$,以验证分布列是否求解正确;求参数时,要注意概率非负。
$6. [2023·$安徽马鞍山二中高二期中$]$设随机变量$ ξ $的分布列为$ P(ξ = i) = a·(\frac{1}{2})^i ( i = 1,2,3 ),$则$ a $的值为
$\frac{8}{7}$
$.$
答案:
6. $\boldsymbol{\frac{8}{7}}$ 【解析】依题意,得$\frac{a}{2}+\frac{a}{4}+\frac{a}{8}=\frac{7a}{8}=1$(利用随机变量的概率和为$1$,求出参数),解得$a = \frac{8}{7}$。所以$a$的值为$\frac{8}{7}$。
7. (多选)[2023·山东潍坊高二期中]以下选项,服从两点分布的随机变量 $ X $ 是(
A.抛掷一枚均匀的骰子,所得点数 $ X $
B.某运动员罚球命中的概率为 0.8,命中得 1 分,不中得 0 分,罚球一次的得分 $ X $
C.从装有大小完全相同的 5 个红球、3 个白球的袋中任取 1 个球,$ X = \begin{cases}1,取出白球, \\ 0,取出红球 \end{cases} $
D.从含有 3 件次品的 100 件产品中随机抽取一件,$ X $ 为抽到的次品件数
BCD
)A.抛掷一枚均匀的骰子,所得点数 $ X $
B.某运动员罚球命中的概率为 0.8,命中得 1 分,不中得 0 分,罚球一次的得分 $ X $
C.从装有大小完全相同的 5 个红球、3 个白球的袋中任取 1 个球,$ X = \begin{cases}1,取出白球, \\ 0,取出红球 \end{cases} $
D.从含有 3 件次品的 100 件产品中随机抽取一件,$ X $ 为抽到的次品件数
答案:
7. BCD 【解析】对于 A,$X = 1,2,3,4,5,6$,所以不是两点分布;对于 B,$X = 0,1$,是两点分布;对于 C,$X = 0,1$,是两点分布;对于 D,抽取一次,则或为正品或为次品,故$X = 0,1$,是两点分布。故选 BCD。
8. [2023·河南郑州高二期中]设某项试验的成功率是失败率的 3 倍,用随机变量 $ X $ 去描述 1 次试验的成功次数,则 $ P(X = 1) = $(
A.0
B.$ \frac{1}{4} $
C.$ \frac{2}{3} $
D.$ \frac{3}{4} $
D
)A.0
B.$ \frac{1}{4} $
C.$ \frac{2}{3} $
D.$ \frac{3}{4} $
答案:
8. D 【解析】由已知得$X$的所有可能取值为$0,1$,且$P(X = 1)=3P(X = 0)$,代入$P(X = 1)+P(X = 0)=1$(两点分布只有两个结果,且概率和为$1$),得$P(X = 1)+\frac{1}{3}P(X = 1)=1$,所以$P(X = 1)=\frac{3}{4}$。故选 D。
$9. [2023·$河北保定高二期中$]$已知离散型随机变量$ X $服从两点分布$,$且$ P(X = 0) = 3 - 4P(X = 1) = a ,$则$ a = $
$\frac{1}{3}$
$.$
答案:
9. $\boldsymbol{\frac{1}{3}}$ 【解析】因为$X$服从两点分布,所以$P(X = 0)+P(X = 1)=1$。因为$P(X = 0)=3 - 4P(X = 1)=a$,所以$P(X = 0)=3 - 4[1 - P(X = 0)]=a$,所以$P(X = 0)=a = \frac{1}{3}$。
10. [2022·甘肃天水第一中学高二月考]设 $ X $ 是一个离散型随机变量,其分布列如表,则 $ q $ 等于(
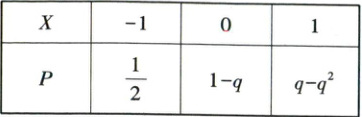
A.1
B.$ \frac{\sqrt{2}}{2} $ 或 $ -\frac{\sqrt{2}}{2} $
C.$ 1 + \frac{\sqrt{2}}{2} $
D.$ \frac{\sqrt{2}}{2} $
D
)
A.1
B.$ \frac{\sqrt{2}}{2} $ 或 $ -\frac{\sqrt{2}}{2} $
C.$ 1 + \frac{\sqrt{2}}{2} $
D.$ \frac{\sqrt{2}}{2} $
答案:
10. D 【解析】由离散型随机变量分布列的性质得$\begin{cases}\frac{1}{2}+1 - q + q - q^2 = 1, \\ 0 \leq 1 - q \leq 1, \\ 0 \leq q - q^2 \leq 1,\end{cases}$解得$q = \frac{\sqrt{2}}{2}$。故选 D。
易错规避 随机变量的分布列的概率要满足两个条件,一是每个概率都在区间$[0,1]$内,二是所有概率和为$1$。
易错规避 随机变量的分布列的概率要满足两个条件,一是每个概率都在区间$[0,1]$内,二是所有概率和为$1$。
查看更多完整答案,请扫码查看


