2025年练习生高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. [2023·上海徐汇南洋中学高二期末]抛三枚质地均匀的硬币,其中恰好有两枚正面朝上的概率为(
A.$ \dfrac{1}{4} $
B.$ \dfrac{3}{8} $
C.$ \dfrac{1}{2} $
D.$ \dfrac{5}{8} $
B
)A.$ \dfrac{1}{4} $
B.$ \dfrac{3}{8} $
C.$ \dfrac{1}{2} $
D.$ \dfrac{5}{8} $
答案:
1.B【解析】每枚硬币正面朝上的概率都是$\frac{1}{2}$,故抛三枚硬币,其中恰好有两枚正面朝上的概率$p = \mathrm{C}_{3}^{2} × \left(\frac{1}{2}\right)^{2} × \frac{1}{2} = \frac{3}{8}$。故选B。
2. 甲、乙两人下棋,根据以往总共20次的对弈记录,甲取胜10次,乙取胜10次.两人进行一场五局三胜的比赛,最终胜者赢得200元奖金.第一局、第二局比赛都是甲胜,现在比赛因意外终止.鉴于公平,应该分给甲奖金(
A.100元
B.150元
C.175元
D.200元
C
)A.100元
B.150元
C.175元
D.200元
答案:
2.C【解析】由题意知,甲、乙获胜的概率都是$\frac{1}{2}$,假设比赛继续,甲只需三场中赢得一场即获得全额奖金,甲获胜的概率$p = 1 - \left(1 - \frac{1}{2}\right)^{3} = \frac{7}{8}$,所以甲应获奖金$200 × \frac{7}{8} = 175$(元)。故选C。
3. [2023·辽宁沈阳高二期末]已知 $ X\sim B\left(4,\dfrac{1}{3}\right) $,则 $ P(X = 1) = $(
A.$ \dfrac{8}{81} $
B.$ \dfrac{32}{81} $
C.$ \dfrac{4}{27} $
D.$ \dfrac{8}{27} $
B
)A.$ \dfrac{8}{81} $
B.$ \dfrac{32}{81} $
C.$ \dfrac{4}{27} $
D.$ \dfrac{8}{27} $
答案:
3.B【解析】因为$X \sim B\left(4, \frac{1}{3}\right)$,所以$P(X = 1) = \mathrm{C}_{4}^{1} × \frac{1}{3} × \left(\frac{2}{3}\right)^{3} = \frac{32}{81}$。故选B。
4. [2023·上海杨浦高级中学高三开学考试]设随机变量 $ \xi\sim B(2,p) $,$ \eta\sim B(3,p) $,若 $ P(\xi\geqslant 1)=\dfrac{5}{9} $,则 $ P(\eta\geqslant 2)= $
$\frac{7}{27}$
.
答案:
4.$\frac{7}{27}$【解析】$\because$随机变量$\xi \sim B(2, p)$,且$P(\xi \geq 1) = \frac{5}{9}$,$\therefore P(\xi \geq 1) = 1 - P(\xi = 0) = 1 - \mathrm{C}_{2}^{0} · (1 - p)^{2} = \frac{5}{9}$,解得$p = \frac{1}{3}$,$\therefore \eta \sim B\left(3, \frac{1}{3}\right)$,$\therefore P(\eta \geq 2) = 1 - P(\eta = 0) - P(\eta = 1) = 1 - \mathrm{C}_{3}^{0} \left(\frac{1}{3}\right)^{0} \left(\frac{2}{3}\right)^{3} - \mathrm{C}_{3}^{1} \left(\frac{1}{3}\right)^{1} \left(\frac{2}{3}\right)^{2} = 1 - \frac{8}{27} - \frac{4}{9} = \frac{7}{27}$(正难则反,简化计算)。
5. [2023·上海浦东高二期末]小明和小王在课余进行象棋比赛,采用“五局三胜制”或“三局两胜制”定胜负.相对而言,小明棋艺稍弱,每一局赢的概率都为0.4.小明为了让自己在比赛中赢的概率更大些,应该提议采用
三局两胜制
.(填“三局两胜制”或“五局三胜制”)
答案:
5.三局两胜制【解析】因为小明每一局赢的概率都为$0.4$,所以采用“三局两胜制”时小明获胜的概率为$\mathrm{C}_{2}^{2} × (0.4)^{2} + \mathrm{C}_{2}^{1} × 0.4 × 0.6 × 0.4 = 0.352$,采用“五局三胜制”时小明获胜的概率为$\mathrm{C}_{3}^{3} × 0.4^{3} + \mathrm{C}_{3}^{2} × 0.4^{2} × 0.6 × 0.4 + \mathrm{C}_{3}^{2} × 0.4^{2} × 0.6^{2} × 0.4 = 0.31744$,所以小明选择“三局两胜制”获胜概率更大。
6. [2023·浙江杭州高三开学考试]第二十二届世界杯足球赛于2022年11月21日在卡塔尔举行,是历史上首次在中东国家境内举行,也是第二次在亚洲举行的世界杯足球赛.在火热的氛围中,某商场设计了一款足球游戏:场地上共有大、小2个球门,依次对大门和小门射门,射进大门后才能射小门,两次均进球可得到一个世界杯吉祥物“拉伊卜”.已知甲、乙、丙射进大门的概率均为$ \dfrac{3}{4} $,射进小门的概率依次为$ \dfrac{2}{3} $,$ \dfrac{1}{3} $,$ \dfrac{1}{3} $,假设各次进球与否互不影响.
(1)求这3人中至少有2人射进大门的概率;
(2)记这3人中得到“拉伊卜”的人数为$ X $,求$ X $的分布列.
(1)求这3人中至少有2人射进大门的概率;
(2)记这3人中得到“拉伊卜”的人数为$ X $,求$ X $的分布列.
答案:
6.【解】
(1)设3人中射进大门的人数为$Y$,则$Y \sim B\left(3, \frac{3}{4}\right)$,$\therefore P(Y \geq 2) = P(Y = 2) + P(Y = 3) = \mathrm{C}_{3}^{2} × \left(\frac{3}{4}\right)^{2} × \frac{1}{4} + \left(\frac{3}{4}\right)^{3} = \frac{27}{32}$。
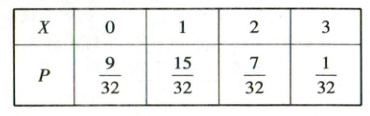
(2)甲获得“拉伊卜”的概率$p_{1} = \frac{3}{4} × \frac{2}{3} = \frac{1}{2}$,乙、丙获得“拉伊卜”的概率$p_{2} = \frac{3}{4} × \frac{1}{3} = \frac{1}{4}$。由题意,$X$的可能取值为$0, 1, 2, 3$,则$P(X = 0) = \left(1 - \frac{1}{2}\right) × \left(1 - \frac{1}{4}\right)^{2} = \frac{9}{32}$,$P(X = 1) = \frac{1}{2} × \left(1 - \frac{1}{4}\right)^{2} + \left(1 - \frac{1}{2}\right) × \mathrm{C}_{2}^{1} × \frac{1}{4} × \left(1 - \frac{1}{4}\right) = \frac{15}{32}$,$P(X = 2) = \mathrm{C}_{2}^{1} × \frac{1}{2} × \frac{1}{4} × \left(1 - \frac{1}{4}\right) + \left(1 - \frac{1}{2}\right) × \left(\frac{1}{4}\right)^{2} = \frac{7}{32}$,$P(X = 3) = \frac{1}{2} × \left(\frac{1}{4}\right)^{2} = \frac{1}{32}$,$\therefore X$的分布列如下表:
| $X$ | $0$ | $1$ | $2$ | $3$ |
| --- | --- | --- | --- | --- |
| $P$ | $\frac{9}{32}$ | $\frac{15}{32}$ | $\frac{7}{32}$ | $\frac{1}{32}$ |
(1)设3人中射进大门的人数为$Y$,则$Y \sim B\left(3, \frac{3}{4}\right)$,$\therefore P(Y \geq 2) = P(Y = 2) + P(Y = 3) = \mathrm{C}_{3}^{2} × \left(\frac{3}{4}\right)^{2} × \frac{1}{4} + \left(\frac{3}{4}\right)^{3} = \frac{27}{32}$。
(2)甲获得“拉伊卜”的概率$p_{1} = \frac{3}{4} × \frac{2}{3} = \frac{1}{2}$,乙、丙获得“拉伊卜”的概率$p_{2} = \frac{3}{4} × \frac{1}{3} = \frac{1}{4}$。由题意,$X$的可能取值为$0, 1, 2, 3$,则$P(X = 0) = \left(1 - \frac{1}{2}\right) × \left(1 - \frac{1}{4}\right)^{2} = \frac{9}{32}$,$P(X = 1) = \frac{1}{2} × \left(1 - \frac{1}{4}\right)^{2} + \left(1 - \frac{1}{2}\right) × \mathrm{C}_{2}^{1} × \frac{1}{4} × \left(1 - \frac{1}{4}\right) = \frac{15}{32}$,$P(X = 2) = \mathrm{C}_{2}^{1} × \frac{1}{2} × \frac{1}{4} × \left(1 - \frac{1}{4}\right) + \left(1 - \frac{1}{2}\right) × \left(\frac{1}{4}\right)^{2} = \frac{7}{32}$,$P(X = 3) = \frac{1}{2} × \left(\frac{1}{4}\right)^{2} = \frac{1}{32}$,$\therefore X$的分布列如下表:
| $X$ | $0$ | $1$ | $2$ | $3$ |
| --- | --- | --- | --- | --- |
| $P$ | $\frac{9}{32}$ | $\frac{15}{32}$ | $\frac{7}{32}$ | $\frac{1}{32}$ |
7. 某学校举行跳跃运动比赛,规则如下:假设比赛过程中每位选手需要进行2次三周及三周以上的跳跃动作,其中甲的三周跳跃动作成功率为0.7,成功完成动作后得8分,失败得4分;甲的四周跳跃动作成功率为0.3,成功完成动作后得15分,失败得6分(每次跳跃动作是否成功相互独立).
(1)若甲选择先进行一次三周跳跃动作,再进行一次四周跳跃动作,求甲的得分高于14分的概率;
(2)若甲选择连续进行两次三周跳跃动作,$ Y $表示甲的最终得分,求随机变量$ Y $的分布列.
(1)若甲选择先进行一次三周跳跃动作,再进行一次四周跳跃动作,求甲的得分高于14分的概率;
(2)若甲选择连续进行两次三周跳跃动作,$ Y $表示甲的最终得分,求随机变量$ Y $的分布列.
答案:
7.【解】
(1)设甲第$k$次动作成功完成为事件$A_{k}(k = 1, 2)$,甲选择先进行一次三周跳跃动作,再进行一次四周跳跃动作,得分高于14分的情况有:三周跳跃动作与四周跳跃动作都成功;三周跳跃动作失败与四周跳跃动作成功。所以甲的得分高于14分的概率$p = P(A_{1}A_{2}) + P(\overline{A_{1}}A_{2}) = 0.7 × 0.3 + 0.3 × 0.3 = 0.3$。
(2)甲两次动作成功与否相互独立,且成功率均为$0.7$。设$X$为成功完成动作的次数,故$X \sim B(2, 0.7)$,甲选择连续进行两次三周跳跃动作都失败得8分;甲选择连续进行两次三周跳跃动作成功一次得12分;甲选择连续进行两次三周跳跃动作都成功得16分。故$P(Y = 8) = P(X = 0) = \mathrm{C}_{2}^{0} 0.7^{0} × 0.3^{2} = 0.09$,$P(Y = 12) = P(X = 1) = \mathrm{C}_{2}^{1} 0.7^{1} × 0.3^{1} = 0.42$,$P(Y = 16) = P(X = 2) = \mathrm{C}_{2}^{2} 0.7^{2} × 0.3^{0} = 0.49$,所以随机变量$Y$的分布列如下:
7.【解】
(1)设甲第$k$次动作成功完成为事件$A_{k}(k = 1, 2)$,甲选择先进行一次三周跳跃动作,再进行一次四周跳跃动作,得分高于14分的情况有:三周跳跃动作与四周跳跃动作都成功;三周跳跃动作失败与四周跳跃动作成功。所以甲的得分高于14分的概率$p = P(A_{1}A_{2}) + P(\overline{A_{1}}A_{2}) = 0.7 × 0.3 + 0.3 × 0.3 = 0.3$。
(2)甲两次动作成功与否相互独立,且成功率均为$0.7$。设$X$为成功完成动作的次数,故$X \sim B(2, 0.7)$,甲选择连续进行两次三周跳跃动作都失败得8分;甲选择连续进行两次三周跳跃动作成功一次得12分;甲选择连续进行两次三周跳跃动作都成功得16分。故$P(Y = 8) = P(X = 0) = \mathrm{C}_{2}^{0} 0.7^{0} × 0.3^{2} = 0.09$,$P(Y = 12) = P(X = 1) = \mathrm{C}_{2}^{1} 0.7^{1} × 0.3^{1} = 0.42$,$P(Y = 16) = P(X = 2) = \mathrm{C}_{2}^{2} 0.7^{2} × 0.3^{0} = 0.49$,所以随机变量$Y$的分布列如下:

查看更多完整答案,请扫码查看


