《2025年练习生高中数学选择性必修第二册人教B版》

12. 如图，在某城市中，M，N 两地之间有整齐的方格形道路网，其中$A_{1}$，$A_{2}$，$A_{3}$，$A_{4}$是道路网中位于一条对角线上的 4 个交汇点。今在道路网 M，N 处的甲、乙两人分别要到 N，M 处，他们分别随机地选择一条沿街的最短路径，以相同的速度同时出发，直到到达 N，M 处为止，则下列说法正确的有(BD)

A.甲从 M 到达 N 处的走法种数为 120
B.甲从 M 经过$A_{3}$到达 N 处的走法种数为 9
C.甲、乙两人能在$A_{3}$处相遇的走法种数为 36
D.甲、乙两人能相遇的走法种数为 164

答案： 12. BD 【解析】对于A，甲从M到N，需要走6格，其中向上3格，向右3格，所以从M到达N处的走法种数为$\mathrm{C}_{6}^{3} = 20$，故A错误。对于B，甲从M到达$A_{3}$，需要走3格，其中向上1格，向右2格，有$\mathrm{C}_{3}^{1} = 3$（种）走法，从$A_{3}$到达N，需要走3格，其中向上2格，向右1格，有$\mathrm{C}_{3}^{2} = 3$（种）走法，所以甲从M经过$A_{3}$到达N处的走法种数为$3 × 3 = 9$，故B正确。对于C，甲经过$A_{3}$的走法种数为$\mathrm{C}_{3}^{1} × \mathrm{C}_{3}^{2} = 9$，乙经过$A_{3}$的走法种数为$\mathrm{C}_{3}^{1} × \mathrm{C}_{3}^{2} = 9$，所以甲、乙两人能在$A_{3}$处相遇的走法种数为$9 × 9 = 81$，故C错误。对于D，甲、乙两人沿着最短路径行走，只能在$A_{1}, A_{2}, A_{3}, A_{4}$处相遇。若甲、乙两人在$A_{1}$处相遇，甲经过$A_{1}$处，必须向上走3格，乙经过$A_{1}$处，必须向左走3格，两人在$A_{1}$处相遇的走法有1种；若甲、乙两人在$A_{2}$或$A_{3}$处相遇，各有81种走法；若甲、乙两人在$A_{4}$处相遇，甲经过$A_{4}$处，必须向右走3格，乙经过$A_{4}$处，必须向下走3格，则两人在$A_{4}$处相遇的走法有1种。所以甲、乙两人能相遇的走法种数为$1 + 81 + 81 + 1 = 164$，故D正确。选BD。

13. [2022·上海南洋模范中学高三月考]将编号为 1，2，3，4 的四个小球放到三个不同的盒子里，每个盒子至少放一个小球且编号为 1，2 的两个小球不能放到同一个盒子里，则不同放法的种数有30。(用数字作答)

答案： 13. 30 【解析】由题意，得四个小球有两个放在同一个盒子里的方法数是$\mathrm{C}_{4}^{2}$。把这两个球看作一个整体同另外两个球全排列，有$\mathrm{A}_{3}^{3}$种结果。而编号为1，2号小球放在同一个盒子里有$\mathrm{A}_{3}^{3} = 6$（种）放法，所以编号为1，2的两个小球不放到同一个盒子里的放法种数是$\mathrm{C}_{4}^{2}\mathrm{A}_{3}^{3} - 6 = 30$。

14. $(1 + \sqrt[3]{x})^{6}(1 + \frac{1}{\sqrt[4]{x}})^{10}$展开式中的常数项为4246。

答案： 14. 4246 【解析】$(1 + \sqrt[3]{x})^{6}$的通项公式为$T_{r + 1} = \mathrm{C}_{6}^{r}· (x^{\frac{1}{3}})^{r} = \mathrm{C}_{6}^{r}x^{\frac{r}{3}}$，$r = 0, 1, 2, 3, 4, 5, 6$。$\left(1 + \frac{1}{\sqrt[4]{x}}\right)^{10}$的通项公式为$T_{k + 1} = \mathrm{C}_{10}^{k}(x^{-\frac{1}{4}})^{k} = \mathrm{C}_{10}^{k}x^{-\frac{k}{4}}$，$k = 0, 1, 2, 3, 4, ·s, 10$。两通项公式相乘，得$\mathrm{C}_{6}^{r}x^{\frac{r}{3}}\mathrm{C}_{10}^{k}x^{-\frac{k}{4}} = \mathrm{C}_{6}^{r}\mathrm{C}_{10}^{k}x^{\frac{r}{3} - \frac{k}{4}}$。令$\frac{r}{3} - \frac{k}{4} = 0$，得$4r = 3k$。所以满足条件的$(r, k)$有三组，为$(0, 0)$，$(3, 4)$，$(6, 8)$。所以常数项为$1 + \mathrm{C}_{6}^{3}\mathrm{C}_{10}^{4} + \mathrm{C}_{6}^{6}\mathrm{C}_{10}^{8} = 4246$。

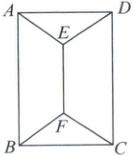
15. 如图，给图中的 A，B，C，D，E，F 共 6 个点涂色，要求每个点涂 1 种颜色，且图中每条线段的 2 个端点涂不同颜色。若有 4 种颜色可供选择，则不同的涂色方法共有264种。

答案： 15. 264 【解析】计算不同涂色方法数分为两类。第一类，当涂4种颜色时，先涂A，E，D，有$\mathrm{A}_{4}^{3}$种涂法，再从B，F，C中选1个点涂第4种颜色，如B，再涂F。若F与D同色，则C有2种涂法；若F与D异色，则C有1种涂法，所以有$\mathrm{A}_{4}^{3}\mathrm{C}_{3}^{1}· (2 + 1)$种涂法。第二类，当涂3种颜色时，先涂A，E，D，有$\mathrm{C}_{4}^{3}· \mathrm{A}_{3}^{3}$种涂法，再涂B，有2种涂法，则F，C各有1种涂法，所以有$2\mathrm{C}_{4}^{3}\mathrm{A}_{3}^{3}$种涂法。利用分类加法计数原理，得不同涂色方法共有$\mathrm{A}_{4}^{3}\mathrm{C}_{3}^{1}(2 + 1) + 2\mathrm{C}_{4}^{3}\mathrm{A}_{3}^{3} = 216 + 48 = 264$（种）。

16. [2022·江苏宿迁沭阳高级中学高二月考]已知$f(x) = (1 + x)^{m} + (1 + x)^{n}(m \in \mathbf{N}_{+},n \in \mathbf{N}_{+})$，$f(x)$的展开式中含$x$项的系数为 11，则当$m =$6或5时，含$x^{2}$项的系数有最小值，为25。

答案： 16. 6或5 25 【解析】$(1 + x)^{m}$的通项公式为$T_{r + 1} = \mathrm{C}_{m}^{r}x^{r}$，含$x$项的系数为$\mathrm{C}_{m}^{1} = m$。$(1 + x)^{n}$的通项公式为$T_{k + 1} = \mathrm{C}_{n}^{k}x^{k}$，含$x$项的系数为$\mathrm{C}_{n}^{1} = n$。由题意可得$m + n = 11$。当$m$，$n$中有一个为1时，不妨设$n = 1$，则$m = 10$，则$f(x)$的展开式中含$x^{2}$项的系数为$\mathrm{C}_{m}^{2} = \mathrm{C}_{10}^{2} = 45$。当$m$，$n$都大于或等于2时，$f(x)$的展开式中含$x^{2}$项的系数为$\mathrm{C}_{m}^{2} + \mathrm{C}_{n}^{2}$。因为$\mathrm{C}_{m}^{2} + \mathrm{C}_{n}^{2} = \frac{m(m - 1)}{2} + \frac{n(n - 1)}{2} = \frac{m^{2} + n^{2} - (m + n)}{2} = \frac{(m + n)^{2} - 2mn - (m + n)}{2} = \frac{121 - 11 - 2mn}{2} = m^{2} - 11m + 55 = \left(m - \frac{11}{2}\right)^{2} + \frac{99}{4}$，且$m \in \mathrm{Z}$，所以当$m = 6$或$m = 5$时，含$x^{2}$项的系数取得最小值，为25。

17. （本小题满分 10 分）在某次国际高峰论坛上，组委会要从 6 个国内媒体团和 3 个国外媒体团中选出 3 个媒体团进行提问。要求这 3 个媒体团中既有国内媒体团又有国外媒体团，且国内媒体团不能连续提问，则不同的提问方式的种数是多少？

答案： 17. 解：结合题意，根据选取方式可分为两类。
第一类，有2个国内媒体团和1个国外媒体团，选取方式有$\mathrm{C}_{6}^{2}\mathrm{C}_{3}^{1}$种，提问方式有$\mathrm{A}_{2}^{2}$种，共有$\mathrm{C}_{6}^{2}\mathrm{C}_{3}^{1}\mathrm{A}_{2}^{2} = 90$（种）不同的提问方式。
第二类，有1个国内媒体团和2个国外媒体团，选取方式有$\mathrm{C}_{6}^{1}\mathrm{C}_{3}^{2}$种，提问方式有$\mathrm{A}_{3}^{3}$种，共有$\mathrm{C}_{6}^{1}\mathrm{C}_{3}^{2}\mathrm{A}_{3}^{3} = 108$（种）不同的提问方式。
综上可知，共有$90 + 108 = 198$（种）不同的提问方式。

18. （本小题满分 12 分）[2022·山东烟台第二中学高二月考]在$(\sqrt{x} + \frac{2}{x^{2}})^{5}$的展开式中，求：
（1）展示式中的第 3 项；
（2）展开式中二项式系数最大的项。

答案： 18. 解：
(1)$\left(\sqrt{x} + \frac{2}{x^{2}}\right)^{5}$的展开式的第3项为$\mathrm{C}_{5}^{2}· \left(x^{\frac{1}{2}}\right)^{5 - 2}· (2x^{-2})^{2} = 2^{2}· \mathrm{C}_{5}^{2}· x^{-\frac{5}{2}} = 40x^{-\frac{5}{2}}$。
(2)对于二项式$\left(\sqrt{x} + \frac{2}{x^{2}}\right)^{5}$，因为$n = 5$，所以第3项和第4项的二项式系数最大，其中第3项为$40x^{-\frac{5}{2}}$，第4项为$\mathrm{C}_{5}^{3}· \left(x^{\frac{1}{2}}\right)^{5 - 3}· (2x^{-2})^{3} = 2^{3}· \mathrm{C}_{5}^{3}· x^{-5} = 80x^{-5}$。