《2025年练习生高中数学选择性必修第二册人教B版》

11. [2023·内蒙古阿拉善盟第一中学高三期末]端午节为每年农历五月初五，是中国人民纪念屈原的传统节日. 小华的妈妈为小华煮了 8 个粽子，其中 5 个甜茶粽和 3 个艾香粽，小华随机取出 2 个，事件 $A$ 表示“取到的两个为同一种粽子”，事件 $B$ 表示“取到的两个都是艾香粽”，则 $P(B|A)=$(B)

A.$\frac{3}{5}$
B.$\frac{3}{13}$
C.$\frac{5}{8}$
D.$\frac{13}{28}$

答案： 11. B 【解析】由题意，得$ P(A) = \frac{\mathrm{C}_5^2 + \mathrm{C}_3^2}{\mathrm{C}_8^2} = \frac{13}{28} $，$ P(AB) = \frac{\mathrm{C}_3^2}{\mathrm{C}_8^2} = \frac{3}{28} $，所以$ P(B|A) = \frac{P(AB)}{P(A)} = \frac{\frac{3}{28}}{\frac{13}{28}} = \frac{3}{13} $。故选 B。

12. [2023·广东广州高二期中]某单位组织晚会活动，甲、乙、丙、丁 4 名员工采用抽签法决定表演顺序，在“员工甲不是第一个表演，员工乙不是最后一个表演”的条件下，员工丙第一个表演的概率为(B)

A.$\frac{3}{13}$
B.$\frac{2}{7}$
C.$\frac{1}{4}$
D.$\frac{1}{5}$

答案： 12. B 思维路径 根据条件概率公式求出事件“员工甲不是第一个表演，员工乙不是最后一个表演”的概率→可分为两类，员工甲最后一个表演或员工甲不是最后一个表演→再求出“员工丙第一个表演，员工乙不是最后一个表演”的概率。\n 【解析】设事件$ A $为“员工甲不是第一个表演，员工乙不是最后一个表演”，事件$ B $为“员工丙第一个表演”。事件$ A $分两类：员工甲最后一个表演，则剩下的 3 名员工可以随便排序，方法数为$ \mathrm{A}_3^3 $；员工甲不是最后一个表演，则中间两个位置选一个位置为甲，然后剩下的位置除了最后一个位置，选一个位置给乙，其余的员工随便排，方法数为$ \mathrm{C}_2^1\mathrm{C}_2^1\mathrm{A}_2^2 $，故$ P(A) = \frac{\mathrm{A}_3^3 + \mathrm{C}_2^1\mathrm{C}_2^1\mathrm{A}_2^2}{\mathrm{A}_4^4} = \frac{14}{24} = \frac{7}{12} $。员工甲不是第一个表演，员工乙不是最后一个表演，员工丙是第一个表演，则先排员工丙在第一个位置，然后除了第一个位置和最后一个位置选一个位置给乙，剩下的两个员工随便排，方法数为$ \mathrm{C}_2^1\mathrm{A}_2^2 $，故$ P(AB) = \frac{\mathrm{C}_2^1\mathrm{A}_2^2}{\mathrm{A}_4^4} = \frac{4}{24} = \frac{1}{6} $。综上，$ P(B|A) = \frac{P(AB)}{P(A)} = \frac{\frac{1}{6}}{\frac{7}{12}} = \frac{2}{7} $。故选 B。

13. [2023·云南曲靖高三第一次教学质量监测]若 $a$，$b\in\{1,2,3\}$，则在“函数 $f(x)=\ln(x^{2}+ax + b)$ 的定义域为 $\mathbf{R}$”的条件下，“函数 $g(x)=a^{x}-b^{-x}$ 为奇函数”的概率为(C)

A.$\frac{1}{6}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{2}{3}$

答案： 13. C 思维路径 函数$ f(x) = \ln(x^2 + ax + b) $的定义域为$ \mathrm{R} \to \forall x \in \mathrm{R} $，$ x^2 + ax + b ＞ 0 $恒成立$ \to a^2 ＜ 4b \to $根据$ g(x) = a^x - b^{-x} $为奇函数得出$ a = b $或$ ab = 1 \to $再根据条件概率的计算公式即可计算出结果。\n 【解析】用所有的有序数对$ (a, b) $表示满足$ a, b \in \{1, 2, 3\} $的情况，则所有的情况为$ (1,1) $，$ (1,2) $，$ (1,3) $，$ (2,1) $，$ (2,2) $，$ (2,3) $，$ (3,1) $，$ (3,2) $，$ (3,3) $，共 9 种。记“函数$ f(x) = \ln(x^2 + ax + b) $的定义域为$ \mathrm{R} $”为事件$ A $。因为函数$ f(x) = \ln(x^2 + ax + b) $的定义域为$ \mathrm{R} $，所以$ \forall x \in \mathrm{R} $，$ x^2 + ax + b ＞ 0 $恒成立，即$ \Delta = a^2 - 4b ＜ 0 $，即$ a^2 ＜ 4b $，其中满足$ a^2 ＜ 4b $的基本事件有$ (1,1) $，$ (1,2) $，$ (1,3) $，$ (2,2) $，$ (2,3) $，$ (3,3) $，共 6 种，故$ P(A) = \frac{6}{9} = \frac{2}{3} $。记“函数$ g(x) = a^x - b^{-x} $为奇函数”为事件$ B $。已知$ g(x) $是奇函数，且定义域为$ \mathrm{R} $，则$ g(1) = -g(-1) $，即$ a - \frac{1}{b} = -\frac{1}{a} + b $，即$ a - b = \frac{a - b}{ab} $，解得$ a = b $或$ ab = 1 $。满足$ a = b $或$ ab = 1 $的情况有$ (1,1) $，$ (2,2) $，$ (3,3) $，共 3 种，所以同时满足事件$ A $和事件$ B $的情况有$ (1,1) $，$ (2,2) $，$ (3,3) $，共 3 种，所以$ P(AB) = \frac{3}{9} = \frac{1}{3} $，所以$ P(B|A) = \frac{P(AB)}{P(A)} = \frac{\frac{1}{3}}{\frac{2}{3}} = \frac{1}{2} $。故选 C。

14. (多选)某校开展“一带一路”知识竞赛，甲组有 8 名选手，其中 5 名男生，3 名女生；乙组有 8 名选手，其中 4 名男生，4 名女生. 现从甲组随机抽取 1 人加入乙组，再从乙组随机抽取 1 人，$A_{1}$ 表示“从甲组抽取的是男生”，$A_{2}$ 表示“从甲组抽取的是女生”，$B$ 表示“从乙组抽取的是女生”，则(BC)

A.$A_{1}$，$A_{2}$ 不是对立事件
B.$P(B)=\frac{35}{72}$
C.$P(\overline{B}|A_{1})=\frac{5}{9}$
D.$P(B|A_{2})=\frac{4}{9}$

答案： 14. BC 【解析】对于 A 选项，根据对立事件的概念可知，$ A_1 $，$ A_2 $是对立事件，A 错误；对于 B 选项，由题意可知，$ P(B) = \frac{5}{8} × \frac{4}{9} + \frac{3}{8} × \frac{5}{9} = \frac{35}{72} $（求概率时，可利用分步乘法计数原理求解），B 正确；对于 C 选项，当$ A_1 $发生时，从乙组抽取 1 人有 9 种可能情况，其中抽取的不是女生的情况有 5 种，则$ P(\overline{B}|A_1) = \frac{5}{9} $，C 正确；对于 D 选项，当$ A_2 $发生时，从乙组抽取 1 人有 9 种可能情况，其中抽取的是女生的情况有 5 种，则$ P(B|A_2) = \frac{5}{9} $，D 错误。故选 BC。

15. 一个不透明的袋子中装有大小、质地完全相同的 4 个小球，小球上分别标有数字 1，2，3，4，若从袋子中一次性取出 2 个小球，在已知取出的小球上数字之和小于 6 的情况下，取出的小球上的数字为一奇一偶的概率为$\frac{3}{4}$.

答案： 15. $\frac{3}{4}$ 【解析】从袋子中一次性取出 2 个小球的样本空间$ \Omega = \{(1,2), (1,3), (1,4), (2,3), (2,4), (3,4)\} $。设事件$ A $为“取出的 2 个小球上的数字之和小于 6”，则$ A = \{(1,2), (1,3), (1,4), (2,3)\} $（当事件比较少时，可利用列举法求解），即$ n(A) = 4 $。设事件$ B $为“取出的 2 个小球上的数字为一奇一偶”，则$ B = \{(1,2), (1,4), (2,3), (3,4)\} $，则$ AB = \{(1,2), (1,4), (2,3)\} $，即$ n(AB) = 3 $，所以$ P(B|A) = \frac{n(AB)}{n(A)} = \frac{3}{4} $。

16. [2023·浙江十校联盟高三联考]已知随机事件 $A$，$B$，$P(A)=\frac{1}{3}$，$P(B)=\frac{1}{4}$，$P(A|B)=\frac{3}{4}$，则 $P(\overline{B}|A)=$$\frac{7}{16}$.

答案： 16. $\frac{7}{16}$ 【解析】由题意得$ P(A|B) = \frac{P(AB)}{P(B)} = \frac{3}{4} $，所以$ P(AB) = \frac{3}{4}P(B) = \frac{3}{4} × \frac{1}{4} = \frac{3}{16} $，故$ P(B|A) = \frac{P(AB)}{P(A)} = \frac{\frac{3}{16}}{\frac{1}{3}} = \frac{9}{16} $，所以$ P(\overline{B}|A) = 1 - P(B|A) = \frac{7}{16} $。

17. [2023·湖北高三联考]第二十四届冬季奥林匹克运动会在北京顺利举行，为推广滑雪运动 深入了解湖北某地中小学学生在“自由式滑雪”和“单板滑雪”两项活动的参与情况，随机选取了 10 所学校进行研究，得到如下图数据：

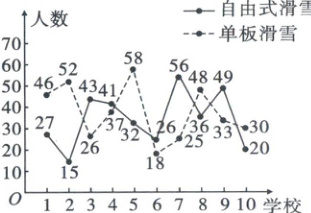
(1)在这 10 所学校中随机选取 3 所来调查研究，求在抽到学校至少有一个参与“自由式滑雪”超过 40 人的条件下，“单板滑雪”不超过 30 人的概率.
(2)现在有一个“单板滑雪”集训营，对“滑行、转弯、停止”这 3 个动作技巧进行集训，且在集训中进行了多轮测试. 规定：在一轮测试中，这 3 个动作中至少有 2 个动作达到“优秀”. 则该轮测试记为“优秀”，在集训测试中，小明同学滑行、转弯、停止三个动作达到“优秀”的概率分别为 $\frac{2}{3}$，$\frac{1}{2}$，$\frac{1}{3}$，且各个动作互不影响、每轮测试互不影响. 求小明同学在一轮测试中为“优秀”的概率.

答案： 17. 【解】
(1)由题可知 10 个学校参与“自由式滑雪”的人数依次为 27，15，43，41，32，26，56，36，49，20，参与“单板滑雪”的人数依次为 46，52，26，37，58，18，25，48，33，30，\n 其中参与“自由式滑雪”的人数超过 40 人的学校有 4 个，参与“自由式滑雪”的人数超过 40 人，且“单板滑雪”的人数超过 30 人的学校有 2 个。\n 设事件$ A $为“从这 10 所学校中抽到的学校至少有一个参与‘自由式滑雪’的人数超过 40 人”，\n 事件$ B $为“从这 10 所学校中选出的 3 所学校中参与‘单板滑雪’的人数不超过 30 人”，\n 则$ P(A) = \frac{\mathrm{C}_4^1\mathrm{C}_6^2 + \mathrm{C}_4^2\mathrm{C}_6^1 + \mathrm{C}_4^3}{\mathrm{C}_{10}^3} = \frac{5}{6} $，$ P(AB) = \frac{\mathrm{C}_2^1\mathrm{C}_2^2 + \mathrm{C}_2^2\mathrm{C}_2^1}{\mathrm{C}_{10}^3} = \frac{1}{30} $，\n 所以$ P(B|A) = \frac{P(AB)}{P(A)} = \frac{\frac{1}{30}}{\frac{5}{6}} = \frac{1}{25} $。\n
(2)由题意可得小明同学在一轮测试中为“优秀”的概率\n $ p = \frac{2}{3} × \frac{1}{2} × \left(1 - \frac{1}{3}\right) + \frac{2}{3} × \left(1 - \frac{1}{2}\right) × \frac{1}{3} + \left(1 - \frac{2}{3}\right) × \frac{1}{2} × \frac{1}{3} + \frac{2}{3} × \frac{1}{2} × \frac{1}{3} = \frac{1}{2} $。