2025年练习生高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列说法正确的是(
A.圆的面积与半径之间的关系是相关关系
B.粮食产量与施肥量之间的关系是函数关系
C.一定范围内,学生的成绩与学习时间呈正相关关系
D.人的体重与视力呈负相关关系
C
)A.圆的面积与半径之间的关系是相关关系
B.粮食产量与施肥量之间的关系是函数关系
C.一定范围内,学生的成绩与学习时间呈正相关关系
D.人的体重与视力呈负相关关系
答案:
1. C 【解析】(破题关键:函数关系是变量之间的确定关系,相关关系是变量之间确实存在关系但不具有确定性)对于A,圆的面积与半径之间的关系是确定的关系,是函数关系,所以A错误;对于B,粮食产量与施肥量之间的关系不是函数关系,是相关关系,所以B错误;对于C,一定范围内,学生的成绩与学习时间呈正相关关系,所以C正确;对于D,人的体重与视力是没有相关关系的,所以D错误。故选C。
方法总结 两个变量是否相关的两种判断方法
(1)根据实际经验:借助积累的经验进行分析判断。
(2)利用散点图:通过散点图,观察它们的分布是否存在一定的规律,直观地进行判断。如果发现点的分布从整体上看大致在一条直线附近,那么这两个变量就是线性相关的,注意不要受个别点的位置的影响。
方法总结 两个变量是否相关的两种判断方法
(1)根据实际经验:借助积累的经验进行分析判断。
(2)利用散点图:通过散点图,观察它们的分布是否存在一定的规律,直观地进行判断。如果发现点的分布从整体上看大致在一条直线附近,那么这两个变量就是线性相关的,注意不要受个别点的位置的影响。
2. [2023·陕西西安铁一中高三期末]如表中给出五组数据$(x,y)$,从中选出四组使其线性相关性最强,且保留第一组$(-5,-3)$,那么应去掉第
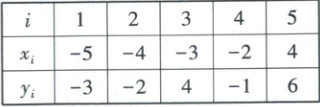
3
组。
答案:
2. 3 【解析】(破题关键:作出散点图,观察图像,所有的点大致在一条直线附近,去掉离直线偏离程度最高的点)根据表格数据,作出散点图如图。

显然点(−3,4)的偏离程度最高,故去掉第3组。
2. 3 【解析】(破题关键:作出散点图,观察图像,所有的点大致在一条直线附近,去掉离直线偏离程度最高的点)根据表格数据,作出散点图如图。

显然点(−3,4)的偏离程度最高,故去掉第3组。
3. [2023·四川雅安高二期末]根据如下样本数据,得到回归直线方程为$y=\hat{b}x+\hat{a}$,则(
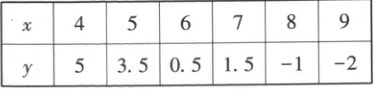
A.$\hat{a}>0,\hat{b}>0$
B.$\hat{a}>0,\hat{b}<0$
C.$\hat{a}<0,\hat{b}>0$
D.$\hat{a}<0,\hat{b}<0$
B
)
A.$\hat{a}>0,\hat{b}>0$
B.$\hat{a}>0,\hat{b}<0$
C.$\hat{a}<0,\hat{b}>0$
D.$\hat{a}<0,\hat{b}<0$
答案:
3. B 【解析】根据表中数据可作出散点图,如图。由散点图可知,随着x的增加y逐渐减小,则y与x是负相关,故回归趋势,当x = 0时与y轴截距为正,则â> 0。故选B。
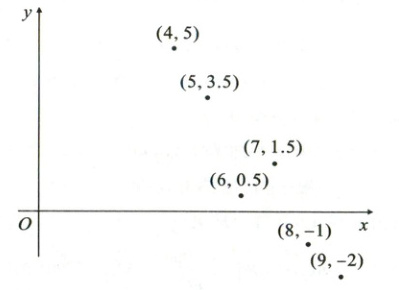
3. B 【解析】根据表中数据可作出散点图,如图。由散点图可知,随着x的增加y逐渐减小,则y与x是负相关,故回归趋势,当x = 0时与y轴截距为正,则â> 0。故选B。
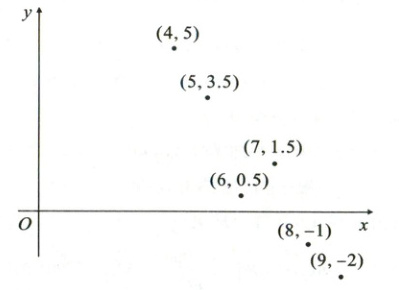
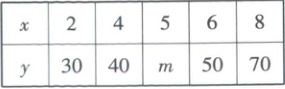
4. [2023·陕西西安高三模拟]根据变量$x$与$y$的对应关系(如表),求得$y$关于$x$的回归直线方程为$\hat{y}=6.5x+17.5$,则表中$m$的值为(
A.$60$
B.$55$
C.$50$
D.$45$
A
)
A.$60$
B.$55$
C.$50$
D.$45$
答案:
4. A 【解析】由表中数据,计算$\bar{x} = \frac{1}{5} × (2 + 4 + 5 + 6 + 8) = 5 $,$\bar{y} = \frac{1}{5} × (30 + 40 + m + 50 + 70) = 38 + \frac{m}{5} $。因为回归直线方程$\hat{y} = 6.5x + 17.5 $过点$(\bar{x}, \bar{y}) $〔求参数时,注意回归直线必过点$(\bar{x}, \bar{y}) $〕,所以$38 + \frac{m}{5} = 6.5 × 5 + 17.5 $,解得$m = 60 $。故选A。
5. [2023·江西赣州高二期中]直播带货已经成为农民创业增收的好帮手,数据显示 2022 年全国农村直播电商已达到 573.2 万家。已知 2022 年某农村电商每月直播销售收入$y$(单位:万元)与月份$x$($x = 1,2,·s,12$)具有线性相关关系,利用该电商全年 12 个月的直播销售月收入数据,求得回归直线方程为$\hat{y}=10+1.2x$,则下列结论一定正确的是(
A.把$x = n(n = 1,2,·s,12)$代入求得的$\hat{y}$是第$n$个月的销售收入
B.相关系数$r = 1.2$
C.2022 年该电商直播销售收入逐月增加
D.该电商 2022 年直播销售总收入为 213.6 万元
D
)A.把$x = n(n = 1,2,·s,12)$代入求得的$\hat{y}$是第$n$个月的销售收入
B.相关系数$r = 1.2$
C.2022 年该电商直播销售收入逐月增加
D.该电商 2022 年直播销售总收入为 213.6 万元
答案:
5. D 【解析】利用$\hat{y} = 10 + 1.2x $求得的是每月直播销售收入的预测数据,与每月直播销售收入的真实数据可能不相同,A,C错误;$1.2 $不是相关系数(相关系数的绝对值不大于1),B错误;$\bar{x} = \frac{1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12}{12} = 6.5 $,由点$(\bar{x}, \bar{y}) $在回归直线上,得$\bar{y} = 10 + 1.2 × 6.5 = 17.8 $,所以该电商2022年直播销售总收入为$17.8 × 12 = 213.6 $(万元)。故选D。
6. [2023·辽宁阜新高二期末]如图是 2013—2022 年全国城镇人口、乡村人口的折线图。根据折线图,下列说法错误的是(

A.城镇人口与年份呈现正相关
B.乡村人口与年份的相关系数$r$接近$1$
C.城镇人口逐年增长率大致相同
D.可预测乡村人口仍呈现下降趋势
B
)
A.城镇人口与年份呈现正相关
B.乡村人口与年份的相关系数$r$接近$1$
C.城镇人口逐年增长率大致相同
D.可预测乡村人口仍呈现下降趋势
答案:
6. B 【解析】对于A选项,由折线图可知,城镇人口与年份呈现正相关,A正确;对于B选项,因为乡村人口与年份呈负线性相关关系,且线性相关性很强,所以$r $接近$ -1 $,B错误;对于C选项,城镇人口与年份呈现正相关,且线性相关性很强,相关系数$r $接近1,故城镇人口逐年增长率大致相同,C正确;对于D选项,由折线图可知,乡村人口与年份呈负线性相关关系,可预测乡村人口仍呈现下降趋势,D正确。故选B。
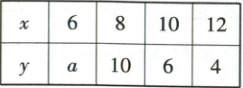
7. (多选)[2023·辽宁辽阳高二期末]已知关于变量$x,y$的$4$组数据如下表。根据表中数据计算得到$x,y$之间的回归直线方程为$\hat{y}=-1.4x+20.6$,$x,y$之间的相关系数为$r$,则(
A.$a = 12$
B.变量$x,y$正相关
C.$r=-\frac{7\sqrt{2}}{10}$
D.$r=-\frac{2\sqrt{2}}{3}$
AC
)
A.$a = 12$
B.变量$x,y$正相关
C.$r=-\frac{7\sqrt{2}}{10}$
D.$r=-\frac{2\sqrt{2}}{3}$
答案:
7. AC 【解析】回归直线必过点$(\bar{x}, \bar{y}) $,$\bar{x} = 9 $,$\bar{y} = -1.4\bar{x} + 20.6 = 8 = \frac{a + 10 + 6 + 4}{4} $,解得$a = 12 $,所以选项A正确。由回归直线方程和表格可知,变量$x, y $负相关,所以选项B错误。$r = \frac{\sum_{i = 1}^{4} (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i = 1}^{4} (x_i - \bar{x})^2 \sum_{i = 1}^{4} (y_i - \bar{y})^2}} = \frac{(-3) × 4 + (-1) × 2 + 1 × (-2) + 3 × (-4)}{\sqrt{9 + 1 + 1 + 9} × \sqrt{16 + 4 + 4 + 16}} = -\frac{7\sqrt{2}}{10} $,所以选项C正确,选项D错误。故选AC。
方法总结 线性回归直线不一定过样本点,但必过样本的中心点$(\bar{x}, \bar{y}) $,常利用这一结论求参数。
方法总结 线性回归直线不一定过样本点,但必过样本的中心点$(\bar{x}, \bar{y}) $,常利用这一结论求参数。
查看更多完整答案,请扫码查看


