《2025年练习生高中数学选择性必修第二册人教B版》

7. [2023·江苏南京第一中学高三期末]已知随机变量 $ X \sim N(\mu, \sigma^{2}) $，且 $ P(|X - \mu| ＜ 1) + P(|X - 2\mu| \geq 1) + P(\mu + 1 \leq X ＜ 2\mu + 1) = 1 $，则 $ \mu = $(B)

A.-1
B.0
C.1
D.2

答案： 7. B 【解析】（破题关键：根据正态曲线的对称性列方程求解）$ P(|X - \mu|\lt 1)=P(\mu - 1\lt X\lt \mu + 1) $，$ P(|X - 2\mu|\geq 1)=P(X\geq 2\mu + 1)+P(X\leq 2\mu - 1) $。因为$ P(|X - \mu|\lt 1)+P(|X - 2\mu|\geq 1)+P(\mu + 1\leq X\leq 2\mu + 1)=P(X\gt \mu - 1)+P(X\leq 2\mu - 1)=1 $，所以$ \mu - 1 = 2\mu - 1 $，解得$ \mu = 0 $。故选 B。

8. [2023·上海格致中学高三开学考试]已知 $ X \sim N(\mu_{1}, \sigma_{1}^{2}) $，$ Y \sim N(\mu_{2}, \sigma_{2}^{2}) $，正态曲线如图。下列结论正确的是(C)


A.$ P(Y \geq \mu_{2}) \geq P(Y \geq \mu_{1}) $
B.$ P(X \leq \sigma_{2}) \leq P(X \leq \sigma_{1}) $
C.对任意正数 $ t $，$ P(X \leq t) \geq P(Y \leq t) $
D.对任意正数 $ t $，$ P(X \geq t) \geq P(Y \geq t) $

答案： 8. C 【解析】由正态曲线的性质可知，$ X\sim N(\mu_{1},\sigma_{1}^{2}) $，$ Y\sim N(\mu_{2},\sigma_{2}^{2}) $，所以$ X $和$ Y $的正态曲线分别关于直线$ x = \mu_{1} $，$ x = \mu_{2} $对称，因此结合所给图像可得$ \mu_{1}\lt \mu_{2} $，$ \therefore P(Y\geq \mu_{2})\lt P(Y\geq \mu_{1}) $。又$ X\sim N(\mu_{1},\sigma_{1}^{2}) $的正态曲线较$ Y\sim N(\mu_{2},\sigma_{2}^{2}) $的正态曲线更“瘦高”，$ \therefore 0\lt \sigma_{1}\lt \sigma_{2} $，$ \therefore P(X\leq \sigma_{2})\gt P(X\leq \sigma_{1}) $。故 A，B 错误。由正态曲线与横轴所围成的图形的面积的意义，知对任意正数$ t $，$ P(X\leq t)\geq P(Y\leq t) $。故 C 正确，D 错误。选 C。
方法总结 对于正态曲线，当期望越大时，则其对称轴越靠右；当方差较大时，图像矮胖，方差较小时，图像高瘦。

9. 已知随机变量 $ \xi \sim N(2, \sigma^{2}) $，且 $ P(\xi \leq 1) = P(\xi \geq a - 1) $，则 $ \frac{1}{x} + \frac{9}{a - x}(0 ＜ x ＜ a) $ 的最小值为(C)

A.9
B.6
C.4
D.2

答案： 9. C 思维路径 由$ P(\xi\leq 1)=P(\xi\geq a - 1) $，得$ a = 4 $→结合基本不等式→利用“1”的代换→得解。
【解析】由随机变量$ \xi\sim N(2,\sigma^{2}) $，得正态曲线的对称轴为直线$ x = 2 $。因为$ P(\xi\leq 1)=P(\xi\geq a - 1) $，所以$ 1 + (a - 1)=4 $，得$ a = 4 $。当$ 0\lt x\lt 4 $时，$ \frac{1}{x}\gt 0 $，$ \frac{9}{4 - x}\gt 0 $，所以有$ \frac{1}{x}+\frac{9}{4 - x}=\left( \frac{1}{x}+\frac{9}{4 - x} \right)×\frac{x + (4 - x)}{4}=\left( 10 + \frac{4 - x}{x}+\frac{9x}{4 - x} \right)×\frac{1}{4}\geq\frac{10 + 2\sqrt{9}}{4}=4 $，当且仅当$ \frac{4 - x}{x}=\frac{9x}{4 - x} $，即$ x = 1 $时等号成立，最小值为 4。故选 C。

10. [2023·福建漳州高二期中]某工厂一台设备生产一种特定零件，工厂为了解该设备的生产情况，随机抽检了该设备在一个生产周期中的 100 件产品的关键指标（单位：cm），经统计得到如下的频率分布直方图。

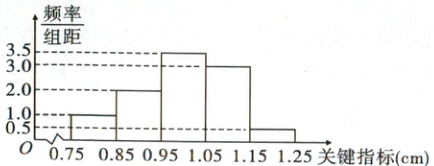
(1)由频率分布直方图估计抽检样本关键指标的平均数 $ \overline{x} $ 和方差 $ s^{2} $。（用每组的中点代表该组的均值）
(2)已知这台设备正常状态下生产零件的关键指标服从正态分布 $ N(\mu, \sigma^{2}) $，用直方图的平均数估计值 $ \overline{x} $ 作为 $ \mu $ 的估计值 $ \hat{\mu} $，用直方图的标准差估计值 $ s $ 作为 $ \sigma $ 估计值 $ \hat{\sigma} $。
①为了监控该设备的生产过程，每个生产周期中都要随机抽测 10 个零件的关键指标，如果出现了关键指标在 $ (\mu - 3\sigma, \mu + 3\sigma) $ 之外的零件，就认为生产过程可能出现了异常，需停止生产并检查设备。下面是某个生产周期中抽测的 10 个零件的关键指标：

利用 $ \hat{\mu} $ 和 $ \hat{\sigma} $ 判断该生产周期是否需停止生产并检查设备。
②若设备状态正常，记 $ X $ 表示一个生产周期内抽取的 10 个零件关键指标在 $ (\mu - 3\sigma, \mu + 3\sigma) $ 之外的零件个数，求 $ P(X \geq 1) $ 及 $ X $ 的数学期望。
附：若随机变量 $ X $ 服从正态分布 $ N(\mu, \sigma^{2}) $，则 $ P(\mu - 3\sigma \leq X \leq \mu + 3\sigma) \approx 0.997 $，$ \sqrt{0.011} \approx 1.05 $，$ \sqrt{0.012} \approx 0.110 $，$ 0.997^{9} \approx 0.9733 $，$ 0.997^{10} \approx 0.9704 $。

答案： 10.【解】
(1)由频率分布直方图，得$ \overline{x}=0.8× 0.1 + 0.9× 0.2 + 1× 0.35 + 1.1× 0.3 + 1.2× 0.05 = 1 $。$ s^{2}=(0.8 - 1)^{2}× 0.1 + (0.9 - 1)^{2}× 0.2 + (1 - 1)^{2}× 0.35 + (1.1 - 1)^{2}× 0.3 + (1.2 - 1)^{2}× 0.05 = 0.011 $。
(2)①由
(1)可知$ \hat{\mu}=1 $，$ \hat{\sigma}=\sqrt{0.011}\approx 0.105 $，所以$ \hat{\mu}-3\hat{\sigma}=1 - 0.315 = 0.685 $，$ \hat{\mu}+3\hat{\sigma}=1 + 0.315 = 1.315 $。显然抽查中的零件指标$ 1.33\gt 1.315 $，故需停止生产并检查设备（当小概率事件发生时，则说明生产有问题，即$ 3\sigma $原则）。
②抽测一个零件关键指标在$ (\mu - 3\sigma,\mu + 3\sigma) $之内的概率为 0.997，所以抽测一个零件关键指标在$ (\mu - 3\sigma,\mu + 3\sigma) $之外的概率为$ 1 - 0.997 = 0.003 $，故$ X\sim B(10,0.003) $，所以$ P(X\geq 1)=1 - P(X = 0)=1 - 0.997^{10}\approx 1 - 0.9704 = 0.0296 $，$ X $的数学期望$ E(X)=10× 0.003 = 0.03 $。