2025年练习生高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. [2022·福建厦门海沧实验中学高二期中]元旦来临之际,某寝室 4 人各写一张贺卡,先集中起来,然后每人从中拿一张别人送出的贺卡,则 4 张贺卡不同的分配方式有(
A.6 种
B.9 种
C.11 种
D.23 种
B
)A.6 种
B.9 种
C.11 种
D.23 种
答案:
10. B 【解析】设四人 A,B,C,D 写的贺卡分别是$a, b, c, d$。当 A 拿贺卡$b$时,B 可以拿$a, c, d$中的任何一张,即 B 拿$a$,C 拿$d$,D 拿$c$,或 B 拿$c$,D 拿$a$,C 拿$d$,或 B 拿$d$,C 拿$a$,D 拿$c$,所以 A 拿$b$时有 3 种不同的分配方式。同理,A 拿$c, d$时也各有 3 种不同的分配方式。由分类加法计数原理,可知 4 张贺卡不同的分配方式有$3 + 3 + 3 = 9$(种)。故选 B。
11. 将 1,2,3,…,9 这 9 个数字填在如图的 9 个空格中,要求每一行从左到右、每一列从上到下增大。当 3,4 固定在图中的位置时,填写空格的方法有(

A.6 种
B.12 种
C.18 种
D.24 种
A
)
A.6 种
B.12 种
C.18 种
D.24 种
答案:
11. A 【解析】由题意,填写空格可分三个步骤:第一步,数字$1, 2, 9$必须放在如图的位置,只有 1 种方法。第二步,数字 5 可以放在左下角或右上角 2 个位置,故数字 5 有 2 种方法。
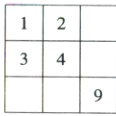
第三步,数字 6 如果和数字 5 相邻,则放数字$7, 8$有 1 种方法;数字 6 如果不和数字 5 相邻,则放数字$7, 8$有 2 种方法,故放数字$6, 7, 8$共有 3 种方法。根据分步乘法计数原理,有$1×2×3 = 6$(种)填写空格的方法。故选 A。
11. A 【解析】由题意,填写空格可分三个步骤:第一步,数字$1, 2, 9$必须放在如图的位置,只有 1 种方法。第二步,数字 5 可以放在左下角或右上角 2 个位置,故数字 5 有 2 种方法。

第三步,数字 6 如果和数字 5 相邻,则放数字$7, 8$有 1 种方法;数字 6 如果不和数字 5 相邻,则放数字$7, 8$有 2 种方法,故放数字$6, 7, 8$共有 3 种方法。根据分步乘法计数原理,有$1×2×3 = 6$(种)填写空格的方法。故选 A。
12. 某日,甲、乙、丙三个单位被系统随机预约到 A,B,C 三家医院接种疫苗且每个单位只能被随机预约到一家医院,每家医院每日至多接待两个单位。已知 A 医院接种的是只需要打一针的腺病毒载体疫苗,B 医院接种的是需要打两针的灭活疫苗,C 医院接种的是需要打三针的重组蛋白疫苗,则甲单位不接种需要打三针的重组蛋白疫苗的预约方案种数为(
A.27
B.24
C.18
D.16
D
)A.27
B.24
C.18
D.16
答案:
12. D 【解析】由题意,甲单位不接种需要打三针的重组蛋白疫苗,即甲不可预约 C 医院,则甲可预约 A,B 两家医院。若甲预约 A 医院,乙预约 A 医院,则丙可预约 B,C 医院,共 2 种方案;若甲预约 A 医院,乙预约 B 或 C 医院,则丙可预约 A,B,C 医院,共$2×3 = 6$(种)方案;若甲预约 B 医院,乙预约 A 或 C 医院,则丙可预约 A,B,C 医院,共$2×3 = 6$(种)方案;若甲预约 B 医院,乙预约 B 医院,则丙可预约 A,C 医院,共 2 种方案。所以甲单位不接种需要打三针的重组蛋白疫苗的预约方案种数为$2 + 6 + 6 + 2 = 16$。故选 D。
方法总结:应用分类加法计数原理与分步乘法计数原理解决实际问题时,要善于将这两个计数原理有机地融合在一起,实际问题的解决往往是“类中有步”“步中有类”,要同时运用两个计数原理才能完成整个事件。
方法总结:应用分类加法计数原理与分步乘法计数原理解决实际问题时,要善于将这两个计数原理有机地融合在一起,实际问题的解决往往是“类中有步”“步中有类”,要同时运用两个计数原理才能完成整个事件。
13. [2022·江苏盐城高二期末]给四面体 $ ABCD $ 的六条棱涂色,每条棱可涂红、黄、蓝、绿四种颜色中的任意一种,且任意共顶点的两条棱颜色都不相同,则不同的涂色方法种数为(
A.24
B.72
C.96
D.144
C
)A.24
B.72
C.96
D.144
答案:
13. C 思维路径:可用分步乘法计数原理求解本题。第一步涂$DA$→第二步涂$DB$→第三步涂$DC$→第四步涂$AB$时分两类,$AB$与$CD$同色或不同色→得出涂法总数。
【解析】由题意,第一步涂$DA$有 4 种涂法,第二步涂$DB$有 3 种涂法,第三步涂$DC$有 2 种涂法。
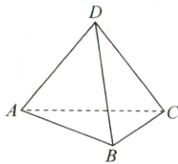
第四步涂$AB$,且$AB$与$DC$同色,则有 1 种涂法。第五步可分为两种情况,若$BC$与$AD$同色,则最后一步涂$AC$有 2 种涂法;若$BC$与$AD$不同色,则最后一步涂$AC$有 1 种涂法。若第四步涂$AB$,且$AB$与$CD$不同色,则$AB$涂第 4 种颜色,此时$BC$,$AC$各有 1 种涂法。综上可知,总的涂法种数是$4×3×2×[1×(2 + 1) + 1×1×1] = 96$。故选 C。
13. C 思维路径:可用分步乘法计数原理求解本题。第一步涂$DA$→第二步涂$DB$→第三步涂$DC$→第四步涂$AB$时分两类,$AB$与$CD$同色或不同色→得出涂法总数。
【解析】由题意,第一步涂$DA$有 4 种涂法,第二步涂$DB$有 3 种涂法,第三步涂$DC$有 2 种涂法。

第四步涂$AB$,且$AB$与$DC$同色,则有 1 种涂法。第五步可分为两种情况,若$BC$与$AD$同色,则最后一步涂$AC$有 2 种涂法;若$BC$与$AD$不同色,则最后一步涂$AC$有 1 种涂法。若第四步涂$AB$,且$AB$与$CD$不同色,则$AB$涂第 4 种颜色,此时$BC$,$AC$各有 1 种涂法。综上可知,总的涂法种数是$4×3×2×[1×(2 + 1) + 1×1×1] = 96$。故选 C。
14. [2022·内蒙古赤峰高二期末]2018 年开始实施新高考考试方案,现模拟选科,其中语文、数学、英语为必选科目,物理、历史两科中选择一科,再从化学、生物学、地理、政治四科中任选两科,组合成“3 + 1 + 2”模式。若小王同学在政治和化学这两科中至多选一科,则他选择的组合方式有
10
种。(用数字作答)
答案:
14. 10 思维路径:考虑物理、历史两科中选择一科→分情况考虑政治和化学这两科都不选、政治和化学这两科选一科→按照计数原理求解。
【解析】第一步,先考虑物理、历史两科中选择一科,有 2 种选法。第二步,若政治和化学这两科都不选,则选生物学、地理,有 1 种选法;若政治和化学这两科选一科,则生物学、地理也选一科,有$2×2 = 4$(种)选法。所以他选择的组合方式共有$2×(1 + 4) = 10$(种)。
【解析】第一步,先考虑物理、历史两科中选择一科,有 2 种选法。第二步,若政治和化学这两科都不选,则选生物学、地理,有 1 种选法;若政治和化学这两科选一科,则生物学、地理也选一科,有$2×2 = 4$(种)选法。所以他选择的组合方式共有$2×(1 + 4) = 10$(种)。
15. [2022·吉林长春实验中学高二月考]从 1,2,3,4,5,6,7,8,9 这九个数字中任取两个,其中一个作为底数,另一个作为真数,则可以得到不同对数值的个数为
53
。
答案:
15. 53 【解析】由于 1 只能作真数,从其余数字中任取一个数作底数,对数值均为 0,此时有 1 个对数值。从除 1 以外的其余各数任取两数分别作为对数的底数和真数,共能组成$8×7 = 56$(个)对数式,其中$\log_{2}4 = \log_{3}9$,$\log_{4}2 = \log_{9}3$,$\log_{3}2 = \log_{9}4$,$\log_{2}3 = \log_{4}9$,所以不同的对数值的个数为$1 + 56 - 4 = 53$。
16. 现有 5 幅不同的国画,2 幅不同的油画,7 幅不同的水彩画。
(1)从中任选 1 幅画布置房间,有几种不同的选法?
(2)从这些国画、油画、水彩画中各选 1 幅布置房间,有几种不同的选法?
(3)从这些画中选出 2 幅不同种类的画布置房间,有几种不同的选法?
(4)要从甲、乙、丙 3 幅不同的画中选出 2 幅,分别挂在左、右两边墙上的指定位置,共有多少种不同的挂法?
(1)从中任选 1 幅画布置房间,有几种不同的选法?
(2)从这些国画、油画、水彩画中各选 1 幅布置房间,有几种不同的选法?
(3)从这些画中选出 2 幅不同种类的画布置房间,有几种不同的选法?
(4)要从甲、乙、丙 3 幅不同的画中选出 2 幅,分别挂在左、右两边墙上的指定位置,共有多少种不同的挂法?
答案:
16. 【解】
(1)分为三类:
第一类,从国画中选,有 5 种不同的选法;
第二类,从油画中选,有 2 种不同的选法;
第三类,从水彩画中选,有 7 种不同的选法。
根据分类加法计数原理,共有$5 + 2 + 7 = 14$(种)不同的选法。
(2)分为三步:
第一步,从国画中选,有 5 种不同的选法;
第二步,从油画中选,有 2 种不同的选法;
第三步,从水彩画中选,有 7 种不同的选法。
根据分步乘法计数原理,共有$5×2×7 = 70$(种)不同的选法。
(3)分为三类:
第一类是 1 幅选自国画,有 5 种不同的选法;1 幅选自油画,有 2 种不同的选法。
由分步乘法计数原理知,有$5×2 = 10$(种)不同的选法。
第二类是 1 幅选自国画,有 5 种不同的选法;1 幅选自水彩画,有 7 种不同的选法。
由分步乘法计数原理知,有$5×7 = 35$(种)不同的选法。
第三类是 1 幅选自油画,有 2 种不同的选法;1 幅选自水彩画,有 7 种不同的选法。
由分步乘法计数原理知,有$2×7 = 14$(种)不同的选法。
所以根据分类加法计数原理,共有$10 + 35 + 14 = 59$(种)不同的选法。
(4)从 3 幅画中选出 2 幅分别挂在左、右两边墙上,可以分两个步骤完成:
第一步,从 3 幅画中选 1 幅挂在左边墙上,有 3 种选法;
第二步,从剩下的 2 幅画中选 1 幅挂在右边墙上,有 2 种选法。
根据分步乘法计数原理,共有$3×2 = 6$(种)不同的挂法。
(1)分为三类:
第一类,从国画中选,有 5 种不同的选法;
第二类,从油画中选,有 2 种不同的选法;
第三类,从水彩画中选,有 7 种不同的选法。
根据分类加法计数原理,共有$5 + 2 + 7 = 14$(种)不同的选法。
(2)分为三步:
第一步,从国画中选,有 5 种不同的选法;
第二步,从油画中选,有 2 种不同的选法;
第三步,从水彩画中选,有 7 种不同的选法。
根据分步乘法计数原理,共有$5×2×7 = 70$(种)不同的选法。
(3)分为三类:
第一类是 1 幅选自国画,有 5 种不同的选法;1 幅选自油画,有 2 种不同的选法。
由分步乘法计数原理知,有$5×2 = 10$(种)不同的选法。
第二类是 1 幅选自国画,有 5 种不同的选法;1 幅选自水彩画,有 7 种不同的选法。
由分步乘法计数原理知,有$5×7 = 35$(种)不同的选法。
第三类是 1 幅选自油画,有 2 种不同的选法;1 幅选自水彩画,有 7 种不同的选法。
由分步乘法计数原理知,有$2×7 = 14$(种)不同的选法。
所以根据分类加法计数原理,共有$10 + 35 + 14 = 59$(种)不同的选法。
(4)从 3 幅画中选出 2 幅分别挂在左、右两边墙上,可以分两个步骤完成:
第一步,从 3 幅画中选 1 幅挂在左边墙上,有 3 种选法;
第二步,从剩下的 2 幅画中选 1 幅挂在右边墙上,有 2 种选法。
根据分步乘法计数原理,共有$3×2 = 6$(种)不同的挂法。
17. 设 $ A=\{ x|x\geqslant 10,x\in N\} $,$ B\subseteq A $,且 $ B $ 中元素满足:①任意一个元素的各数位的数字互不相同;②任意一个元素的任意两个数位的数字之和不等于 9。
(1)求 $ B $ 中的两位数和三位数的个数。
(2)$ B $ 中是否存在五位数、六位数?
(3)若从小到大排列 $ B $ 中元素,求第 1 081 个元素。
(1)求 $ B $ 中的两位数和三位数的个数。
(2)$ B $ 中是否存在五位数、六位数?
(3)若从小到大排列 $ B $ 中元素,求第 1 081 个元素。
答案:
17. 【解】
(1)两位数中,十位上的数字可取$1, 2, 3, ·s, 9$,个位上的数字由于不能和十位上的数字重复,且与十位上的数字之和不能为 9,故对于十位上的每一个数字,相应的个位数字有 8 种取法,从而满足题意的两位数共有$9×8 = 72$(个)。
对于三位数,我们先考虑百位上的数字,可取$1, 2, 3, ·s, 9$。
再考虑十位上的数字,由于不能与百位上的数字重复,且与百位上的数字之和不能为 9,故有 8 种取法。
最后考虑个位上的数字,由于不能和百位、十位上的数字重复,且和百位、十位上的数字相加都不能等于 9,故有 6 种取法。
从而符合题意的三位数有$9×8×6 = 432$(个)。
(2)五位数存在,如$12\ 340$就是其中一个。
不存在这样的六位数。理由如下:
仿照
(1)的解法,十万位上的数字有 9 种取法,万位上的数字有 8 种取法,千位上的数字有 6 种取法,百位上的数字有 4 种取法,十位上的数字有 2 种取法,个位上的数字有 0 种取法,所以不存在这样的六位数。
(3)由
(1)可得,符合题意的两位数有 72 个,三位数有 432 个。
符合题意的四位数有$9×8×6×4 = 1\ 728$(个)。
四位数中千位上是 1 的有$8×6×4 = 192$(个);
千位上是$2, 3$的也各有 192 个。
因为$1\ 081 - (72 + 432 + 192 + 192 + 192) = 1$(个)。
所以符合题意的数是千位上是 4 的最小的数,即$B$中第$1\ 081$个元素是$4\ 012$。
(1)两位数中,十位上的数字可取$1, 2, 3, ·s, 9$,个位上的数字由于不能和十位上的数字重复,且与十位上的数字之和不能为 9,故对于十位上的每一个数字,相应的个位数字有 8 种取法,从而满足题意的两位数共有$9×8 = 72$(个)。
对于三位数,我们先考虑百位上的数字,可取$1, 2, 3, ·s, 9$。
再考虑十位上的数字,由于不能与百位上的数字重复,且与百位上的数字之和不能为 9,故有 8 种取法。
最后考虑个位上的数字,由于不能和百位、十位上的数字重复,且和百位、十位上的数字相加都不能等于 9,故有 6 种取法。
从而符合题意的三位数有$9×8×6 = 432$(个)。
(2)五位数存在,如$12\ 340$就是其中一个。
不存在这样的六位数。理由如下:
仿照
(1)的解法,十万位上的数字有 9 种取法,万位上的数字有 8 种取法,千位上的数字有 6 种取法,百位上的数字有 4 种取法,十位上的数字有 2 种取法,个位上的数字有 0 种取法,所以不存在这样的六位数。
(3)由
(1)可得,符合题意的两位数有 72 个,三位数有 432 个。
符合题意的四位数有$9×8×6×4 = 1\ 728$(个)。
四位数中千位上是 1 的有$8×6×4 = 192$(个);
千位上是$2, 3$的也各有 192 个。
因为$1\ 081 - (72 + 432 + 192 + 192 + 192) = 1$(个)。
所以符合题意的数是千位上是 4 的最小的数,即$B$中第$1\ 081$个元素是$4\ 012$。
18. 设直线的方程是 $ Ax + By = 0 $,从 1,2,3,4,5 这 5 个数中每次取 2 个不同的数作为 $ A $,$ B $ 的值,则所得不同直线的条数是(
A.20
B.19
C.18
D.16
C
)A.20
B.19
C.18
D.16
答案:
18. C 【解析】从$1, 2, 3, 4, 5$这 5 个数中每次取 2 个不同的数作为$A, B$的值共有$5×4 = 20$(种)结果。在这些直线中有重合的直线,当$A = 1, B = 2$和当$A = 2, B = 4$时,结果相同。把$A, B$交换位置又有一组相同的结果。所以所得不同直线的条数是$20 - 2 = 18$。故选 C。
易错规避:解本题时容易出现重复计算的情况,一定要把相同的直线的条数去掉,避免多算。
易错规避:解本题时容易出现重复计算的情况,一定要把相同的直线的条数去掉,避免多算。
查看更多完整答案,请扫码查看


