《2025年练习生高中数学选择性必修第二册人教B版》

1. [2023·辽宁沈阳第三十一中学高二期末]设随机变量 $ X \sim N(1,2) $，若 $ P(x ＜ a) = P(x ＞ b) $，则 $ a + b = $(D)

A.3
B.4
C.1
D.2

答案： 1. D 【解析】因为随机变量$ X\sim N(1,2) $，且$ P(x\lt a)=P(x\gt b) $，所以由正态曲线的对称性可知，$ \frac{a + b}{2}=1 $，得$ a + b = 2 $。故选 D。

2. (多选)[2023·广东深圳高三期末]已知随机变量 $ X \sim N(\mu, \sigma^{2}) $，函数 $ f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x - \mu)^{2}}{2\sigma^{2}}}(x \in R) $，则(ABC)

A.当 $ x = \mu $ 时，$ f(x) $ 取得最大值 $ \frac{1}{\sigma\sqrt{2\pi}} $
B.曲线 $ y = f(x) $ 关于直线 $ x = \mu $ 对称
C.$ x $ 轴是曲线 $ y = f(x) $ 的渐近线
D.曲线 $ y = f(x) $ 与 $ x $ 轴之间的面积小于 1

答案： 2. ABC 【解析】因为随机变量$ X\sim N(\mu,\sigma^{2}) $，函数$ f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x - \mu)^{2}}{2\sigma^{2}}}(x\in R) $，所以$ f(x) $的对称轴为直线$ x = \mu $，且当$ x = \mu $时，$ f(x) $取最大值为$ \frac{1}{\sigma\sqrt{2\pi}}e^{0}=\frac{1}{\sigma\sqrt{2\pi}} $，故 A，B 正确；根据正态曲线可得，$ x $轴是渐近线，且曲线$ y = f(x) $与$ x $轴所围图形的面积等于 1，故 C 正确，D 错误。选 ABC。
方法总结 正态曲线的最高点坐标为$ \left( \mu,\frac{1}{\sigma\sqrt{2\pi}} \right) $。

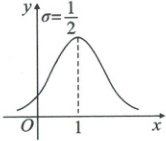
3. [2023·浙江宁波高三二模]设随机变量 $ \xi $ 服从正态分布，相对应的曲线如图，若 $ P(\xi ＜ 0) = p $，则 $ P(0 ＜ \xi ＜ 1) $ 与 $ D(\xi) $ 分别为(C)


A.$ \frac{1}{2} - p, \frac{1}{2} $
B.$ p, \frac{1}{2} $
C.$ \frac{1}{2} - p, \frac{1}{4} $
D.$ p, \frac{1}{4} $

答案： 3. C 【解析】由题意知$ P(\xi\lt 0)=p $，则$ P(0\lt \xi\lt 1)=\frac{1}{2}-p $。由正态曲线得$ \xi\sim N\left( 1,\left( \frac{1}{2} \right)^{2} \right) $（通过图像得出正态分布的具体参数），所以$ D(\xi)=\left( \frac{1}{2} \right)^{2}=\frac{1}{4} $。故选 C。

4. (多选)[2023·江苏南京第五高级中学高二期中]已知在数学测验中，某校学生的成绩服从正态分布 $ N(110, 81) $，其中 90 分为及格线，则下列结论正确的有(ABD)
附：若 $ \xi \sim N(\mu, \sigma^{2}) $，则 $ P(\mu - 2\sigma ＜ \xi ＜ \mu + 2\sigma) = 0.954 $。

A.该校学生成绩的期望为 110
B.该校学生成绩的标准差为 9
C.该校学生成绩的标准差为 81
D.该校学生成绩及格率超过 95%

答案： 4. ABD 【解析】$ \because $该校学生的成绩是服从参数为 110，9 的正态分布，$ \therefore $均值$ \mu = 110 $，方差$ \sigma^{2}=81 $，标准差$ \sigma = 9 $。$ \because \mu - 2\sigma = 110 - 2× 9 = 92 $，$ P(\xi\geq 90)\gt P(\xi\geq 92)=P(\xi\geq \mu - 2\sigma)=\frac{1}{2}+\frac{1}{2}P(\mu - 2\sigma\lt \xi\lt \mu + 2\sigma)=\frac{1}{2}+\frac{1}{2}× 0.954 = 0.977\gt 0.95 $。$ \therefore $该校学生成绩的期望为 110，该校学生成绩的标准差为 9，该校学生成绩及格率超过 95%。故选 ABD。

5. [2023·河南郑州高二期末]已知某高校共有 10 000 名学生，其图书馆阅览室共有 994 个座位，假设学生是否去自习是相互独立的，且每个学生在每天的晚自习时间去阅览室自习的概率均为 0.1。
(1)将每天的晚自习时间去阅览室自习的学生人数记为 $ X $，求 $ X $ 的期望和方差；
(2)数学家棣莫弗发现，当 $ n $ 比较大时，二项分布可视为正态分布。此外，如果随机变量 $ Y \sim N(\mu, \sigma^{2}) $，令 $ Z = \frac{Y - \mu}{\sigma} $，则 $ Z \sim N(0, 1) $。当 $ Z \sim N(0, 1) $ 时，对于任意实数 $ a $，记 $ \varPhi(a) = P(Z ＜ a) $。
①求晚自习时阅览室座位不够用的概率；
②若要使晚自习时阅览室座位够用的概率高于 0.7，则至少需要添加多少个座位？
附：$ \varPhi(0.1) = 0.5398 $，$ \varPhi(0.2) = 0.5793 $，$ \varPhi(0.5) = 0.6915 $，$ \varPhi(0.53) = 0.7019 $。

答案： 5.【解】
(1)由题意可得，随机变量$ X $服从参数为 10 000，0.1 的二项分布，则$ E(X)=np = 10 000× 0.1 = 1 000 $，$ D(X)=np(1 - p)=10 000× 0.1× 0.9 = 900 $。
(2)①由于
(1)中二项分布的$ n $值较大，故可以认为随机变量$ X $服从正态分布。由
(1)可得，$ \mu = 1 000 $，$ \sigma = 30 $，即$ X\sim N(1 000,900) $。将一般正态分布转化为标准正态分布，令$ Z = \frac{X - 1 000}{30} $，则$ Z\sim N(0,1) $，则$ P(X\lt 994)=P(Z\lt - 0.2)=\varPhi(- 0.2) $。由标准正态分布性质可得，$ \varPhi(- 0.2)=1 - \varPhi(0.2) $，则$ P(X\lt 994)=1 - \varPhi(0.2) $，所以$ P(X\gt 994)=1 - P(X\lt 994)=\varPhi(0.2)=0.5793 $，故晚自习时阅览室座位不够用的概率为 0.5793。
②因为$ \varPhi(0.53)=0.7019 $，所以$ P(Z\lt 0.53)=P\left( \frac{X - 1 000}{30}\lt 0.53 \right)=0.7019 $，即$ P(X\lt 1 015.9)=0.7019 $。又$ P(X\lt 1 015)=P\left( \frac{X - 1 000}{30}\lt 0.5 \right)=\varPhi(0.5)=0.6915\lt 0.7 $，所以座位至少要 1 016 个。$ 1 016 - 994 = 22 $（个），故阅览室座位至少需要添加 22 个。
方法总结 若随机变量$ X $服从标准正态分布（$ X\sim N(0,1) $），则有
(1)$ P(X\gt a)=1 - \varPhi(a) $；
(2)$ P(a\lt X\lt b)=\varPhi(b) - \varPhi(a) $；
(3)$ P(|X|\lt a)=2\varPhi(a) - 1 $；
(4)$ P(|X|\gt a)=2\varPhi(- a) $。

6. [2022·福建福州高二期末]已知随机变量 $ Y \sim N(2, 4) $，函数 $ f(x) = P(x \leq Y \leq x + 2) $，则(B)
参考数据：$ P(\mu - \sigma ＜ Y \leq \mu + \sigma) \approx 0.683 $；$ P(\mu - 2\sigma ＜ Y \leq \mu + 2\sigma) \approx 0.954 $。

A.$ f(x) $ 是偶函数
B.$ f(x) $ 的图像关于直线 $ x = 1 $ 对称
C.$ f(x) $ 的图像关于直线 $ x = 2 $ 对称
D.方程 $ f(x) = 0.8 $ 有解

答案： 6. B 【解析】因为$ Y\sim N(2,4) $，所以$ f(x)=P(x\leq Y\leq x + 2)=P(4 - x - 2\leq Y\leq 4 - x)=P(2 - x\leq Y\leq 4 - x)=f(2 - x) $，所以函数$ f(x) $的图像关于直线$ x = 1 $对称，故 A，C 错误，B 正确。由于正态曲线呈现中间高两边低的形状，且关于直线$ x = 1 $对称，故$ f(x)_{\max}=f(1)=P(1\leq Y\leq 3)\lt P(\mu - \sigma\lt Y\leq \mu + \sigma)\approx 0.683 $，因此$ f(x)=0.8 $无解，故 D 错误。选 B。
易错规避 正态曲线关于直线$ x = \mu $对称，在求解概率问题以及与函数的性质相结合的综合问题时，一定要注意这个性质以及数形结合思想的应用。