2025年练习生高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
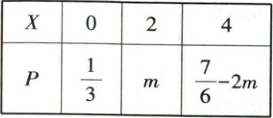
1. [2023·河南新乡高三二模]已知随机变量 $ X $ 的分布列如下表,则 $ E(X) = $ (
A.$ \dfrac{1}{2} $
B.$ 1 $
C.$ \dfrac{4}{3} $
D.$ \dfrac{5}{3} $
D
)
A.$ \dfrac{1}{2} $
B.$ 1 $
C.$ \dfrac{4}{3} $
D.$ \dfrac{5}{3} $
答案:
1. D 【解析】由题可知,$\frac{1}{3}+m+\frac{7}{6}-2m = 1$(分布列的概率和为1),解得$m=\frac{1}{2}$,则$E(X)=0×\frac{1}{3}+2×\frac{1}{2}+4×\frac{1}{6}=\frac{5}{3}$。故选D。
方法总结 求期望时,先判断随机变量是否服从特殊的分布(如超几何分布、二项分布等),若服从,则利用公式求解;若不服从,则求出随机变量的分布列,利用期望的定义$E(X)=\sum_{i = 1}^{n}x_{i}p_{i}(i = 1,2,·s,n)$求解。
方法总结 求期望时,先判断随机变量是否服从特殊的分布(如超几何分布、二项分布等),若服从,则利用公式求解;若不服从,则求出随机变量的分布列,利用期望的定义$E(X)=\sum_{i = 1}^{n}x_{i}p_{i}(i = 1,2,·s,n)$求解。
2. [2023·山西太原高二期中]已知随机变量 $ X $ 的分布列如下表,则随机变量 $ Y = X^2 $ 的数学期望 $ E(Y) = $

2
.
答案:
2. 2 思维路径 由随机变量$X,Y$间的关系$Y = X^{2}$得出$Y$的分布列→结合数学期望公式计算→求得结果。
【解析】由题意知,$X^{2}$的取值为$0,1,4$(先求出$X^{2}$的分布列,再求期望),则$P(Y = 0)=P(X^{2}=0)=0.2$,$P(Y = 1)=P(X^{2}=1)=P(X = 1)+P(X = -1)=0.3 + 0.1 = 0.4$(注意当$Y = 1$时有$X = 1$和$X = -1$两种情况),$P(Y = 4)=P(X^{2}=4)=P(X = 2)=0.4$,所以$Y$的分布列为

故$E(Y)=0×0.2 + 1×0.4 + 4×0.4 = 2$。
2. 2 思维路径 由随机变量$X,Y$间的关系$Y = X^{2}$得出$Y$的分布列→结合数学期望公式计算→求得结果。
【解析】由题意知,$X^{2}$的取值为$0,1,4$(先求出$X^{2}$的分布列,再求期望),则$P(Y = 0)=P(X^{2}=0)=0.2$,$P(Y = 1)=P(X^{2}=1)=P(X = 1)+P(X = -1)=0.3 + 0.1 = 0.4$(注意当$Y = 1$时有$X = 1$和$X = -1$两种情况),$P(Y = 4)=P(X^{2}=4)=P(X = 2)=0.4$,所以$Y$的分布列为

故$E(Y)=0×0.2 + 1×0.4 + 4×0.4 = 2$。
3. [2023·广西河池高二期末]若随机变量 $ \xi $ 的分布列为 $ P(\xi = k) = ck, k = 1, 2, 3, 4 $,其中 $ c $ 是常数,则 $ D(\xi) $ 的值为 (
A.$ \dfrac{4}{5} $
B.$ \dfrac{6}{5} $
C.$ 1 $
D.$ \dfrac{8}{5} $
C
)A.$ \dfrac{4}{5} $
B.$ \dfrac{6}{5} $
C.$ 1 $
D.$ \dfrac{8}{5} $
答案:
3. C 思维路径 通过$\sum_{k = 1}^{4}P(\xi = k)=1$求得参数$k$的值→得到$E(\xi)$→求出$D(\xi)$。
【解析】$\because P(\xi = k)=ck,k = 1,2,3,4$,$\therefore 10c = 1$,解得$c=\frac{1}{10}$。$\therefore E(\xi)=1×\frac{1}{10}+2×\frac{2}{10}+3×\frac{3}{10}+4×\frac{4}{10}=3$,$\therefore D(\xi)=(1 - 3)^{2}×\frac{1}{10}+(2 - 3)^{2}×\frac{2}{10}+(3 - 3)^{2}×\frac{3}{10}+(4 - 3)^{2}×\frac{4}{10}=1$。故选C。
【解析】$\because P(\xi = k)=ck,k = 1,2,3,4$,$\therefore 10c = 1$,解得$c=\frac{1}{10}$。$\therefore E(\xi)=1×\frac{1}{10}+2×\frac{2}{10}+3×\frac{3}{10}+4×\frac{4}{10}=3$,$\therefore D(\xi)=(1 - 3)^{2}×\frac{1}{10}+(2 - 3)^{2}×\frac{2}{10}+(3 - 3)^{2}×\frac{3}{10}+(4 - 3)^{2}×\frac{4}{10}=1$。故选C。
4. [2023·江苏南通高二期末]投资甲、乙两种股票,每种股票收益(单位:元)的分布列如下表,则下列说法正确的是 (
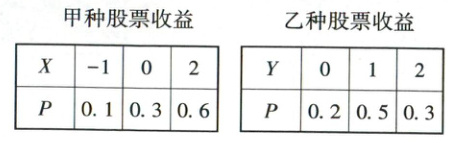
A.投资甲种股票期望收益大
B.投资乙种股票期望收益大
C.投资甲种股票的风险更高
D.投资乙种股票的风险更高
C
)
A.投资甲种股票期望收益大
B.投资乙种股票期望收益大
C.投资甲种股票的风险更高
D.投资乙种股票的风险更高
答案:
4. C 【解析】(破题关键:均值越大,期望收益越大;方差越大,风险越高)甲种股票收益的期望$E(X)= - 1×0.1 + 0×0.3 + 2×0.6 = 1.1$,方差$D(X)=(-1 - 1.1)^{2}×0.1+(0 - 1.1)^{2}×0.3+(2 - 1.1)^{2}×0.6 = 1.29$,乙种股票收益的期望$E(Y)=0×0.2 + 1×0.5 + 2×0.3 = 1.1$,方差$D(Y)=(0 - 1.1)^{2}×0.2+(1 - 1.1)^{2}×0.5+(2 - 1.1)^{2}×0.3 = 0.49$,所以$E(X)=E(Y)$,$D(X)>D(Y)$,则投资甲、乙两种股票的期望收益相等,投资甲种股票比投资乙种股票的风险高。故选C。
5. [2023·江苏常州高二期末]下列说法正确的是 (
A.离散型随机变量的均值是 $[0, 1]$ 上的一个数
B.离散型随机变量的均值反映了随机变量取值的平均水平
C.若离散型随机变量 $ X $ 的均值 $ E(X) = 2 $,则 $ E(2X + 1) = 4 $
D.离散型随机变量 $ X $ 的均值 $ E(X) = \dfrac{x_1 + x_2 + ·s + x_n}{n} $
B
)A.离散型随机变量的均值是 $[0, 1]$ 上的一个数
B.离散型随机变量的均值反映了随机变量取值的平均水平
C.若离散型随机变量 $ X $ 的均值 $ E(X) = 2 $,则 $ E(2X + 1) = 4 $
D.离散型随机变量 $ X $ 的均值 $ E(X) = \dfrac{x_1 + x_2 + ·s + x_n}{n} $
答案:
5. B 【解析】对于A,离散型随机变量的均值是一个常数,不一定在$[0,1]$上(离散型随机变量的均值和概率是两个不同的概念),故A错误;对于B,离散型随机变量的均值反映了随机变量取值的平均水平,故B正确;对于C,离散型随机变量$X$的均值$E(X)=2$,则$E(2X + 1)=2E(X)+1 = 5$,故C错误;对于D,离散型随机变量$X$的均值$E(X)=\sum_{i = 1}^{n}x_{i}p_{i}$,故D错误。选B。
6. [2023·黑龙江绥化高二期末]设随机变量 $ \xi $ 的分布列如下表,且 $ \eta = 2\xi + 5 $,则 $ E(\eta) $ 等于 (

A.$ \dfrac{7}{6} $
B.$ \dfrac{17}{6} $
C.$ \dfrac{17}{3} $
D.$ \dfrac{32}{3} $
D
)
A.$ \dfrac{7}{6} $
B.$ \dfrac{17}{6} $
C.$ \dfrac{17}{3} $
D.$ \dfrac{32}{3} $
答案:
6. D 【解析】依题意可得$E(\xi)=1×\frac{1}{6}+2×\frac{1}{6}+3×\frac{1}{3}+4×\frac{1}{3}=\frac{17}{6}$,所以$E(\eta)=E(2\xi + 5)=2E(\xi)+5 = 2×\frac{17}{6}+5=\frac{32}{3}$。故选D。
7. [2023·云南昆明高二期中]若随机变量 $ X $ 的分布列如下表,且 $ E(X) = 2 $,则 $ D(2X - 3) = $ (

A.$ 2 $
B.$ 3 $
C.$ 4 $
D.$ 5 $
C
)
A.$ 2 $
B.$ 3 $
C.$ 4 $
D.$ 5 $
答案:
7. C 【解析】由分布列的性质知$p = 1 - \frac{1}{6} - \frac{1}{3}=\frac{1}{2}$,则$E(X)=0×\frac{1}{6}+2×\frac{1}{2}+a×\frac{1}{3}=2$,解得$a = 3$。$\therefore D(X)=(0 - 2)^{2}×\frac{1}{6}+(2 - 2)^{2}×\frac{1}{2}+(3 - 2)^{2}×\frac{1}{3}=1$,则$D(2X - 3)=2^{2}D(X)=4$。故选C。
方法总结 若随机变量$X$的数学期望为$E(X)$,方差为$D(X)$,$\eta = aX + b$,则$E(\eta)=E(aX + b)=aE(X)+b$,$D(\eta)=D(aX + b)=a^{2}D(X)$。若随机变量$Y$的数学期望为$E(Y)$,则$E(X + Y)=E(X)+E(Y)$。
方法总结 若随机变量$X$的数学期望为$E(X)$,方差为$D(X)$,$\eta = aX + b$,则$E(\eta)=E(aX + b)=aE(X)+b$,$D(\eta)=D(aX + b)=a^{2}D(X)$。若随机变量$Y$的数学期望为$E(Y)$,则$E(X + Y)=E(X)+E(Y)$。
8. [2023·山西朔州怀仁一中高二期中]已知 $ E(X) + E(2X + 1) = 8 $,则 $ E(X) = $
$\frac{7}{3}$
.
答案:
8. $\frac{7}{3}$ 【解析】由$E(X)+E(2X + 1)=E(X)+2E(X)+1 = 8$,解得$E(X)=\frac{7}{3}$。
9. [2023·河南郑州外国语学校高三模拟]已知随机变量 $ X \sim B\left(4, \dfrac{1}{3}\right) $,下列表达式正确的是 (
A.$ P(X = 2) = \dfrac{4}{81} $
B.$ E(3X + 1) = 4 $
C.$ D(3X + 1) = 8 $
D.$ D(X) = \dfrac{4}{9} $
C
)A.$ P(X = 2) = \dfrac{4}{81} $
B.$ E(3X + 1) = 4 $
C.$ D(3X + 1) = 8 $
D.$ D(X) = \dfrac{4}{9} $
答案:
9. C 【解析】因为$X\sim B\left(4,\frac{1}{3}\right)$,所以$E(X)=4×\frac{1}{3}=\frac{4}{3}$,$D(X)=4×\frac{1}{3}×\left(1 - \frac{1}{3}\right)=\frac{8}{9}$,因此$E(3X + 1)=3E(X)+1 = 3×\frac{4}{3}+1 = 5$,$D(3X + 1)=3^{2}× D(X)=9×\frac{8}{9}=8$,因此选项B,D不正确,选项C正确。又因为$P(X = 2)=\mathrm{C}_{4}^{2}\left(\frac{1}{3}\right)^{2}\left(1 - \frac{1}{3}\right)^{2}=\frac{8}{27}$,所以选项A不正确,故选C。
10. [2023·山东德州高二期末]已知每门大炮击中目标的概率都是 $ 0.5 $,现有 $ 10 $ 门大炮同时对某一目标各射击一次,记恰好击中目标 $ 3 $ 次的概率为 $ p_A $. 若击中目标记 $ 2 $ 分,记 $ 10 $ 门大炮总得分的期望值为 $ E(A) $,则 $ p_A, E(A) $ 的值分别为(
A.$ \dfrac{15}{128}, 5 $
B.$ \dfrac{15}{128}, 10 $
C.$ \dfrac{15}{256}, 5 $
D.$ \dfrac{15}{256}, 10 $
B
)A.$ \dfrac{15}{128}, 5 $
B.$ \dfrac{15}{128}, 10 $
C.$ \dfrac{15}{256}, 5 $
D.$ \dfrac{15}{256}, 10 $
答案:
10. B 【解析】设10门大炮击中目标的次数为$X$,则根据题意可得$X\sim B\left(10,\frac{1}{2}\right)$(大炮命中目标相互独立,故为二项分布),$\therefore 10$门大炮击中目标的次数期望值为$E(X)=10×\frac{1}{2}=5$,则总得分的期望值$E(A)=E(X)×2 = 10$,$\therefore p_{A}=P(X = 3)=\mathrm{C}_{10}^{3}×\left(\frac{1}{2}\right)^{3}×\left(1 - \frac{1}{2}\right)^{7}=\frac{15}{128}$。故选B。
方法总结 若随机变量$X\sim B(n,p)$,则$E(X)=np$,$D(X)=np(1 - p)$。
方法总结 若随机变量$X\sim B(n,p)$,则$E(X)=np$,$D(X)=np(1 - p)$。
查看更多完整答案,请扫码查看


