2025年练习生高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
33. [2023·辽宁本溪高三模拟]某企业为检查一条流水线的生产情况,随机抽取该流水线上的 $ 40 $ 件产品作为样本测出它们的长度(单位:mm),长度的分组区间为 $ (90, 95] $,$ (95, 100] $,$ (100, 105] $,$ (105, 110] $,$ (110, 115] $. 由此得到如图的频率分布直方图.
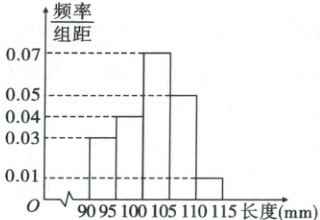
(1)在上述抽取的 $ 40 $ 件产品中任取 $ 2 $ 件,设 $ X $ 为长度超过 $ 105 $ mm 的产品数量,求 $ X $ 的分布列和数学期望;
(2)从该流水线上任取 $ 5 $ 件产品,设 $ Y $ 为长度超过 $ 105 $ mm 的产品数量,求 $ Y $ 的数学期望和方差.

(1)在上述抽取的 $ 40 $ 件产品中任取 $ 2 $ 件,设 $ X $ 为长度超过 $ 105 $ mm 的产品数量,求 $ X $ 的分布列和数学期望;
(2)从该流水线上任取 $ 5 $ 件产品,设 $ Y $ 为长度超过 $ 105 $ mm 的产品数量,求 $ Y $ 的数学期望和方差.
答案:
33. 【解】 (破题关键:$X$服从参数为40,2,12的超几何分布,$Y$服从参数为5,$\frac{3}{10}$的二项分布)
(1)由题意可知,抽取的40件产品中,长度超过105 mm的产品数量为$40×(0.01 + 0.05)×5 = 12$(件)。
所以,随机变量$X$的可能取值为$0,1,2$,
则$P(X = 0)=\frac{\mathrm{C}_{28}^{2}}{\mathrm{C}_{40}^{2}}=\frac{63}{130}$,$P(X = 1)=\frac{\mathrm{C}_{28}^{1}\mathrm{C}_{12}^{1}}{\mathrm{C}_{40}^{2}}=\frac{28}{65}$,$P(X = 2)=\frac{\mathrm{C}_{12}^{2}}{\mathrm{C}_{40}^{2}}=\frac{11}{130}$,
所以随机变量$X$的分布列为
|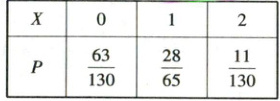
所以$E(X)=0×\frac{63}{130}+1×\frac{28}{65}+2×\frac{11}{130}=\frac{3}{5}$。
(2)由题意可知,$Y\sim B\left(5,\frac{3}{10}\right)$,$\therefore E(Y)=5×\frac{3}{10}=1.5$,$D(Y)=5×\frac{3}{10}×\frac{7}{10}=1.05$。
33. 【解】 (破题关键:$X$服从参数为40,2,12的超几何分布,$Y$服从参数为5,$\frac{3}{10}$的二项分布)
(1)由题意可知,抽取的40件产品中,长度超过105 mm的产品数量为$40×(0.01 + 0.05)×5 = 12$(件)。
所以,随机变量$X$的可能取值为$0,1,2$,
则$P(X = 0)=\frac{\mathrm{C}_{28}^{2}}{\mathrm{C}_{40}^{2}}=\frac{63}{130}$,$P(X = 1)=\frac{\mathrm{C}_{28}^{1}\mathrm{C}_{12}^{1}}{\mathrm{C}_{40}^{2}}=\frac{28}{65}$,$P(X = 2)=\frac{\mathrm{C}_{12}^{2}}{\mathrm{C}_{40}^{2}}=\frac{11}{130}$,
所以随机变量$X$的分布列为
|

所以$E(X)=0×\frac{63}{130}+1×\frac{28}{65}+2×\frac{11}{130}=\frac{3}{5}$。
(2)由题意可知,$Y\sim B\left(5,\frac{3}{10}\right)$,$\therefore E(Y)=5×\frac{3}{10}=1.5$,$D(Y)=5×\frac{3}{10}×\frac{7}{10}=1.05$。
34. [2023·湖南临澧一中高二期中]目前,我国近视人数多达 $ 7 $ 亿,青少年近视率居世界第一. 某中学抽查了 $ 60 $ 名学生的视力情况,按 $[4.0, 4.2)$,$[4.2, 4.4)$,$[4.4, 4.6)$,$[4.6, 4.8)$,$[4.8, 5.0)$,$[5.0, 5.2]$ 分组,制作成如图的频率分布直方图.

(1)为了作进一步的调查,从视力在 $[4.0, 4.4)$ 内的学生中随机抽取 $ 6 $ 人,若已知其中有 $ 2 $ 人的视力落在 $[4.0, 4.2)$ 内,求另外 $ 4 $ 人的视力均落在 $[4.2, 4.4)$ 内的概率;
(2)用样本频率估计总体概率,从全校学生中随机抽取 $ 2 $ 名学生,记视力落在区间 $[4.8, 5.2]$ 内的人数为 $ X $,落在区间 $[4.6, 5.0)$ 内的人数为 $ Y $,试求 $ \dfrac{E(X) + E(Y)}{E(X + Y)} $ 的值.

(1)为了作进一步的调查,从视力在 $[4.0, 4.4)$ 内的学生中随机抽取 $ 6 $ 人,若已知其中有 $ 2 $ 人的视力落在 $[4.0, 4.2)$ 内,求另外 $ 4 $ 人的视力均落在 $[4.2, 4.4)$ 内的概率;
(2)用样本频率估计总体概率,从全校学生中随机抽取 $ 2 $ 名学生,记视力落在区间 $[4.8, 5.2]$ 内的人数为 $ X $,落在区间 $[4.6, 5.0)$ 内的人数为 $ Y $,试求 $ \dfrac{E(X) + E(Y)}{E(X + Y)} $ 的值.
答案:
34. 【解】
(1)视力落在$[4.0,4.2)$内的人数为$60×0.25×0.2 = 3$,
视力落在$[4.2,4.4)$内的人数为$60×0.5×0.2 = 6$。
设事件$A$为抽取的6人中有2人的视力落在$[4.0,4.2)$内,
事件$B$为抽取的6人中有4人的视力落在$[4.2,4.4)$内,
则$P(B|A)=\frac{n(AB)}{n(A)}=\frac{\mathrm{C}_{3}^{2}\mathrm{C}_{6}^{4}}{\mathrm{C}_{3}^{2}\mathrm{C}_{6}^{4}+\mathrm{C}_{3}^{3}\mathrm{C}_{6}^{3}}=\frac{3×15}{3×15 + 20}=\frac{9}{13}$。
(2)随机抽取一名学生,视力落在区间$[4.8,5.2]$内的概率为$0.2×(1 + 1.5)=\frac{1}{2}$,故$X\sim B\left(2,\frac{1}{2}\right)$。
随机抽取一名学生,视力落在区间$[4.6,5.0)$内的概率为$0.2×(1.25 + 1)=\frac{9}{20}$,故$Y\sim B\left(2,\frac{9}{20}\right)$。
所以$E(X)+E(Y)=2×\frac{1}{2}+2×\frac{9}{20}=\frac{19}{10}$。
令$Z = X + Y$,则$Z$的所有可能取值为$0,1,2,3,4$。
易知学生视力落在$[4.0,4.6)$内的概率为$\frac{1}{4}$,落在$[4.6,4.8)\cup[5.0,5.2]$内的概率为$\frac{1}{4}+\frac{3}{10}=\frac{11}{20}$,落在$[4.8,5.0)$内的概率为$\frac{1}{5}$。
当$Z$的值为0时,学生视力落在$[4.0,4.6)$内,则$P(Z = 0)=\mathrm{C}_{2}^{2}\left(\frac{1}{4}\right)^{2}=\frac{1}{16}$;
当$Z$的值为1时,一名学生的视力落在$[4.6,4.8)$或$[5.0,5.2)$内,另一名学生的视力落在$[4.0,4.6)$内,则$P(Z = 1)=\mathrm{C}_{2}^{1}×\frac{1}{4}×\frac{11}{20}=\frac{11}{40}$;
当$Z$的值为2时,一名学生的视力落在$[4.8,5.0)$内,另一名学生的视力落在$[4.0,4.6)$内,或均落在$[4.6,4.8)$或$[5.0,5.2)$内,或一名学生的视力落在$[4.6,4.8)$内,另一名学生的视力落在$[5.0,5.2)$内,则$P(Z = 2)=\mathrm{C}_{2}^{1}×\frac{1}{4}×\frac{1}{5}+\mathrm{C}_{2}^{2}\left(\frac{11}{20}\right)^{2}=\frac{161}{400}$;
当$Z$的值为3时,一名学生的视力落在$[4.6,4.8)$或$[5.0,5.2]$内,另一名学生的视力落在$[4.8,5.0)$内,则$P(Z = 3)=\mathrm{C}_{2}^{1}×\frac{11}{20}×\frac{1}{5}=\frac{11}{50}$;
当$Z$的值为4时,两名学生的视力均落在$[4.8,5.0)$内,则$P(Z = 4)=\mathrm{C}_{2}^{2}\left(\frac{1}{5}\right)^{2}=\frac{1}{25}$。
所以,$E(Z)=0×\frac{1}{16}+1×\frac{11}{40}+2×\frac{161}{400}+3×\frac{11}{50}+4×\frac{1}{25}=\frac{19}{10}$,
故$\frac{E(X)+E(Y)}{E(X + Y)}=\frac{\frac{19}{10}}{\frac{19}{10}}=1$。
方法总结 对于随机变量$X,Y$,我们还有如下结论:$E(X + Y)=E(X)+E(Y)$;若$X,Y$相互独立,则$E(X· Y)=E(X)· E(Y)$。
(1)视力落在$[4.0,4.2)$内的人数为$60×0.25×0.2 = 3$,
视力落在$[4.2,4.4)$内的人数为$60×0.5×0.2 = 6$。
设事件$A$为抽取的6人中有2人的视力落在$[4.0,4.2)$内,
事件$B$为抽取的6人中有4人的视力落在$[4.2,4.4)$内,
则$P(B|A)=\frac{n(AB)}{n(A)}=\frac{\mathrm{C}_{3}^{2}\mathrm{C}_{6}^{4}}{\mathrm{C}_{3}^{2}\mathrm{C}_{6}^{4}+\mathrm{C}_{3}^{3}\mathrm{C}_{6}^{3}}=\frac{3×15}{3×15 + 20}=\frac{9}{13}$。
(2)随机抽取一名学生,视力落在区间$[4.8,5.2]$内的概率为$0.2×(1 + 1.5)=\frac{1}{2}$,故$X\sim B\left(2,\frac{1}{2}\right)$。
随机抽取一名学生,视力落在区间$[4.6,5.0)$内的概率为$0.2×(1.25 + 1)=\frac{9}{20}$,故$Y\sim B\left(2,\frac{9}{20}\right)$。
所以$E(X)+E(Y)=2×\frac{1}{2}+2×\frac{9}{20}=\frac{19}{10}$。
令$Z = X + Y$,则$Z$的所有可能取值为$0,1,2,3,4$。
易知学生视力落在$[4.0,4.6)$内的概率为$\frac{1}{4}$,落在$[4.6,4.8)\cup[5.0,5.2]$内的概率为$\frac{1}{4}+\frac{3}{10}=\frac{11}{20}$,落在$[4.8,5.0)$内的概率为$\frac{1}{5}$。
当$Z$的值为0时,学生视力落在$[4.0,4.6)$内,则$P(Z = 0)=\mathrm{C}_{2}^{2}\left(\frac{1}{4}\right)^{2}=\frac{1}{16}$;
当$Z$的值为1时,一名学生的视力落在$[4.6,4.8)$或$[5.0,5.2)$内,另一名学生的视力落在$[4.0,4.6)$内,则$P(Z = 1)=\mathrm{C}_{2}^{1}×\frac{1}{4}×\frac{11}{20}=\frac{11}{40}$;
当$Z$的值为2时,一名学生的视力落在$[4.8,5.0)$内,另一名学生的视力落在$[4.0,4.6)$内,或均落在$[4.6,4.8)$或$[5.0,5.2)$内,或一名学生的视力落在$[4.6,4.8)$内,另一名学生的视力落在$[5.0,5.2)$内,则$P(Z = 2)=\mathrm{C}_{2}^{1}×\frac{1}{4}×\frac{1}{5}+\mathrm{C}_{2}^{2}\left(\frac{11}{20}\right)^{2}=\frac{161}{400}$;
当$Z$的值为3时,一名学生的视力落在$[4.6,4.8)$或$[5.0,5.2]$内,另一名学生的视力落在$[4.8,5.0)$内,则$P(Z = 3)=\mathrm{C}_{2}^{1}×\frac{11}{20}×\frac{1}{5}=\frac{11}{50}$;
当$Z$的值为4时,两名学生的视力均落在$[4.8,5.0)$内,则$P(Z = 4)=\mathrm{C}_{2}^{2}\left(\frac{1}{5}\right)^{2}=\frac{1}{25}$。
所以,$E(Z)=0×\frac{1}{16}+1×\frac{11}{40}+2×\frac{161}{400}+3×\frac{11}{50}+4×\frac{1}{25}=\frac{19}{10}$,
故$\frac{E(X)+E(Y)}{E(X + Y)}=\frac{\frac{19}{10}}{\frac{19}{10}}=1$。
方法总结 对于随机变量$X,Y$,我们还有如下结论:$E(X + Y)=E(X)+E(Y)$;若$X,Y$相互独立,则$E(X· Y)=E(X)· E(Y)$。
查看更多完整答案,请扫码查看


