2025年练习生高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
15. 下表为某外来生物物种入侵某河流生态后的前$3$个月繁殖数量$y$(单位:只)的数据,通过相关理论进行分析,知可用回归模型$y=e^{1 + a}(a\in R)$对$y$与$t$的关系进行拟合,则根据该回归模型预测第$6$个月该物种的繁殖数量为(

A.$e^{3}$只
B.$e^{3.5}$只
C.$e^{4}$只
D.$e^{4.5}$只
C
)
A.$e^{3}$只
B.$e^{3.5}$只
C.$e^{4}$只
D.$e^{4.5}$只
答案:
15. C 思路路径 将回归模型两边取自然对数得$\ln y = 1 + at \to $令$u = \ln y \to $根据回归直线必过点$(\bar{t}, \bar{u}) \to $求出$a $的值$ \to y = e^{1 + \frac{t}{2}} \to $把$t = 6 $代入$y = e^{1 + \frac{t}{2}} $求解即可。
【解析】由题意,$y = e^{1 + at} $两边取自然对数得$\ln y = 1 + at $,令$u = \ln y $,则$u = 1 + at $。易得$\bar{u} = (\ln y_1 + \ln y_2 + \ln y_3) × \frac{1}{3} = 2 $,$\bar{t} = (t_1 + t_2 + t_3) × \frac{1}{3} = 2 $。$ \because $回归直线必过样本中心点$(\bar{t}, \bar{u}) $,$ \therefore 2 = 2a + 1 $,得$a = \frac{1}{2} $,$ \therefore u = 1 + \frac{t}{2} $,则$y = e^{1 + \frac{t}{2}} $。当$t = 6 $时,$y = e^4 $。故选C。
【解析】由题意,$y = e^{1 + at} $两边取自然对数得$\ln y = 1 + at $,令$u = \ln y $,则$u = 1 + at $。易得$\bar{u} = (\ln y_1 + \ln y_2 + \ln y_3) × \frac{1}{3} = 2 $,$\bar{t} = (t_1 + t_2 + t_3) × \frac{1}{3} = 2 $。$ \because $回归直线必过样本中心点$(\bar{t}, \bar{u}) $,$ \therefore 2 = 2a + 1 $,得$a = \frac{1}{2} $,$ \therefore u = 1 + \frac{t}{2} $,则$y = e^{1 + \frac{t}{2}} $。当$t = 6 $时,$y = e^4 $。故选C。
16. 中国是茶的故乡,也是茶文化的发源地。为了弘扬中国茶文化,某酒店推出特色茶饮品“金萱排骨茶”,为了解每壶“金萱排骨茶”中所放茶叶量$x$(单位:$g$)与食客的满意率$y$的关系,通过调查研究发现可用回归模型$y=\frac{1}{100}e^{kx + c}$来拟合$y$与$x$的关系,根据以下数据:

可求得$y$关于$x$的回归方程为(
A.$\hat{y}=\frac{1}{100}e^{0.043x - 4.291}$
B.$\hat{y}=\frac{1}{100}e^{0.043x + 4.291}$
C.$\hat{y}=\frac{1}{100}e^{-0.043x + 4.291}$
D.$\hat{y}=\frac{1}{100}e^{-0.043x - 4.291}$

可求得$y$关于$x$的回归方程为(
B
)A.$\hat{y}=\frac{1}{100}e^{0.043x - 4.291}$
B.$\hat{y}=\frac{1}{100}e^{0.043x + 4.291}$
C.$\hat{y}=\frac{1}{100}e^{-0.043x + 4.291}$
D.$\hat{y}=\frac{1}{100}e^{-0.043x - 4.291}$
答案:
16. B 【解析】(破题关键:$100y = e^{kx + c} $两边同时取对数转换为$z $关于$x $的线性关系,进而拟合$y $与$x $的关系)对等式$100y = e^{kx + c} $两边同时取对数,可得$z = \ln (100y) = kx + c $。易知$\bar{x} = \frac{1 + 2 + 3 + 4 + 5}{5} = 3 $,$\bar{z} = \frac{4.34 + 4.36 + 4.44 + 4.45 + 4.51}{5} = 4.42 $,则$\sum_{i = 1}^{5} (x_i - \bar{x})^2 = (1 - 3)^2 + (2 - 3)^2 + (3 - 3)^2 + (4 - 3)^2 + (5 - 3)^2 = 10 $,$\sum_{i = 1}^{5} (x_i - \bar{x}) × (z_i - \bar{z}) = (1 - 3) × (4.34 - 4.42) + (2 - 3) × (4.36 - 4.42) + (3 - 3) × (4.44 - 4.42) + (4 - 3) × (4.45 - 4.42) + (5 - 3) × (4.51 - 4.42) = 0.43 $,$k = \frac{\sum_{i = 1}^{5} (x_i - \bar{x})(z_i - \bar{z})}{\sum_{i = 1}^{5} (x_i - \bar{x})^2} = \frac{0.43}{10} = 0.043 $,$c = \bar{z} - k\bar{x} = 4.42 - 0.043 × 3 = 4.291 $。综上,可得$\hat{z} = 0.043x + 4.291 $,又因为$z = \ln (100y) = kx + c $,所以$\hat{y} = \frac{1}{100}e^{0.043x + 4.291} $。故选B。
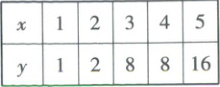
17. [2023·重庆高三二模]设两个相关变量$x$和$y$分别满足下表:
若相关变量$x$和$y$可拟合为非线性回归方程$\hat{y}=2^{bx + \hat{a}}$,则当$x = 6$时,$y$的估计值为(
参考数据:$1.15^{5}\approx2$。
A.$33$
B.$37$
C.$65$
D.$73$
若相关变量$x$和$y$可拟合为非线性回归方程$\hat{y}=2^{bx + \hat{a}}$,则当$x = 6$时,$y$的估计值为(
B
)参考数据:$1.15^{5}\approx2$。

A.$33$
B.$37$
C.$65$
D.$73$
答案:
17. B 思路路径 非线性回归方程化为线性回归方程$ \to $令$\log_2 y = v \to \hat{v} = \hat{b}x + \hat{a} \to $求出$\hat{a}, \hat{b} \to $代入非线性回归方程可得变量$x $和$\hat{y} $之间的关系$ \to $将$x = 6 $代入化简计算即可。
【解析】将非线性回归方程$y = 2^{\hat{b}x + \hat{a}} $转化为线性回归方程,则有$\log_2 y = \hat{b}x + \hat{a} $。令$\log_2 y = v $,即$\hat{v} = \hat{b}x + \hat{a} $,列出相关变量$x, y, v $关系如下:
x 1 2 3 4 5
y 1 2 8 8 16
v 0 1 3 3 4
所以$\sum_{i = 1}^{5} x_i v_i = 0 + 2 + 9 + 12 + 20 = 43 $,$\bar{x} = \frac{1 + 2 + 3 + 4 + 5}{5} = 3 $,$\bar{v} = \frac{0 + 1 + 3 + 3 + 4}{5} = \frac{11}{5} $,$\sum_{i = 1}^{5} x_i^2 = 1 + 4 + 9 + 16 + 25 = 55 $,所以$\hat{b} = \frac{\sum_{i = 1}^{5} x_i v_i - n\bar{x}\bar{v}}{\sum_{i = 1}^{5} x_i^2 - n\bar{x}^2} = \frac{43 - 5 × 3 × \frac{11}{5}}{55 - 5 × 9} = 1 $,所以$\hat{a} = \bar{v} - \hat{b}\bar{x} = \frac{11}{5} - 3 = -\frac{4}{5} $,所以$\hat{v} = x - \frac{4}{5} $,即$\log_2 \hat{y} = x - \frac{4}{5} $,即$\hat{y} = 2^{x - \frac{4}{5}} $。因为$1.15^5 \approx 2 $,所以$2^{\frac{1}{5}} \approx 1.15 $,当$x = 6 $时,$\hat{y} = 2^{6 - \frac{4}{5}} = 2^{\frac{26}{5}} = 2^5 × 2^{\frac{1}{5}} \approx 32 × 1.15 \approx 37 $。故选B。
【解析】将非线性回归方程$y = 2^{\hat{b}x + \hat{a}} $转化为线性回归方程,则有$\log_2 y = \hat{b}x + \hat{a} $。令$\log_2 y = v $,即$\hat{v} = \hat{b}x + \hat{a} $,列出相关变量$x, y, v $关系如下:
x 1 2 3 4 5
y 1 2 8 8 16
v 0 1 3 3 4
所以$\sum_{i = 1}^{5} x_i v_i = 0 + 2 + 9 + 12 + 20 = 43 $,$\bar{x} = \frac{1 + 2 + 3 + 4 + 5}{5} = 3 $,$\bar{v} = \frac{0 + 1 + 3 + 3 + 4}{5} = \frac{11}{5} $,$\sum_{i = 1}^{5} x_i^2 = 1 + 4 + 9 + 16 + 25 = 55 $,所以$\hat{b} = \frac{\sum_{i = 1}^{5} x_i v_i - n\bar{x}\bar{v}}{\sum_{i = 1}^{5} x_i^2 - n\bar{x}^2} = \frac{43 - 5 × 3 × \frac{11}{5}}{55 - 5 × 9} = 1 $,所以$\hat{a} = \bar{v} - \hat{b}\bar{x} = \frac{11}{5} - 3 = -\frac{4}{5} $,所以$\hat{v} = x - \frac{4}{5} $,即$\log_2 \hat{y} = x - \frac{4}{5} $,即$\hat{y} = 2^{x - \frac{4}{5}} $。因为$1.15^5 \approx 2 $,所以$2^{\frac{1}{5}} \approx 1.15 $,当$x = 6 $时,$\hat{y} = 2^{6 - \frac{4}{5}} = 2^{\frac{26}{5}} = 2^5 × 2^{\frac{1}{5}} \approx 32 × 1.15 \approx 37 $。故选B。
18. [2023·浙江宁波高三期末]已知变量$x$和$y$的统计数据如下表:
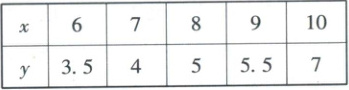
如果由表中数据可得经验回归直线方程为$\hat{y}=0.85x+\hat{a}$,那么$x = 10$时,残差为

如果由表中数据可得经验回归直线方程为$\hat{y}=0.85x+\hat{a}$,那么$x = 10$时,残差为
0.3
。
答案:
18. 0.3 【解析】$\bar{x} = \frac{6 + 7 + 8 + 9 + 10}{5} = 8 $,$\bar{y} = \frac{3.5 + 4 + 5 + 5.5 + 7}{5} = 5 $,所以$\hat{a} = \bar{y} - 0.85\bar{x} = 5 - 0.85 × 8 = -1.8 $,所以$x = 10 $时,$\hat{y}_5 = 0.85 × 10 - 1.8 = 8.5 - 1.8 = 6.7 $,所以残差为$7 - 6.7 = 0.3 $(残差为实际值减去估计值)。
19. [2023·江西南昌二中高二阶段练习]为了研究某疫苗的有效率,在某地进行临床试验,对符合一定条件的$10000$名试验者注射了该疫苗,一周后有$20$人感染,为了验证疫苗的有效率,同期,从相同条件下未注射疫苗的人群中抽取$2500$人,分成$5$组,各组感染人数如下:
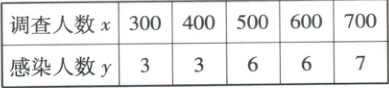
并求得$y$与$x$的回归方程为$\hat{y}=0.011x+\hat{a}$,同期,在人数为$10000$的条件下,以拟合结果估算未注射疫苗人群中感染的人数,记为$N$,注射疫苗后仍被感染的人数记为$n$,则估计该疫苗的有效率为

并求得$y$与$x$的回归方程为$\hat{y}=0.011x+\hat{a}$,同期,在人数为$10000$的条件下,以拟合结果估算未注射疫苗人群中感染的人数,记为$N$,注射疫苗后仍被感染的人数记为$n$,则估计该疫苗的有效率为
0.817
。(疫苗的有效率为$1-\frac{n}{N}$;参考数据:$109.5^{-1}\approx0.009132$;结果保留$3$位有效数字)
答案:
19. 0.817 【解析】由题设表格中的数据可得$\bar{x} = 500 $,$\bar{y} = 5 $,则$\hat{a} = 5 - 0.011 × 500 = -0.5 $,故$N = 0.011 × 10000 - 0.5 = 110 - 0.5 = 109.5 $,而$n = 20 $,故疫苗有效率为$1 - \frac{20}{109.5} \approx 1 - 20 × 0.009132 \approx 0.817 $。
20. 从$2018$年到$2023$年六年间我国公共图书馆机构数与对应年份编号的散点图如图(为便于计算,将$2018—2023$年依次编号为$1,2,·s,6$),并得到回归直线方程为$\hat{y}=13.743x+3095.7$,其相关指数$r^{2}=0.9817$,则下列结论正确的是
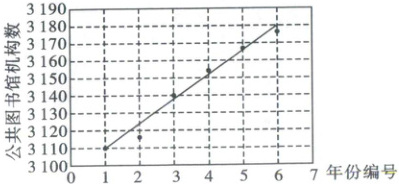
①公共图书馆机构数与年份编号的正相关性较强;
②公共图书馆机构数平均每年增加$13.743$;
③可预测$2024$年公共图书馆机构数为$3192$。
①②③
。(写出所有满足要求的结论编号)
①公共图书馆机构数与年份编号的正相关性较强;
②公共图书馆机构数平均每年增加$13.743$;
③可预测$2024$年公共图书馆机构数为$3192$。
答案:
20. ①②③ 【解析】因为回归直线方程为$\hat{y} = 13.743x + 3095.7 $,斜率为正数13.743,相关指数$r^2 = 0.9817 $,所以公共图书馆机构数与年份编号的正相关性较强,故①正确;根据线性回归方程中$\hat{b} $的实际意义,知公共图书馆机构数平均每年增加13.743,故②正确;当$x = 7 $时,$\hat{y} = 13.743 × 7 + 3095.7 = 3191.901 \approx 3192 $,故预测2024年公共图书馆机构数为3192,③正确。
查看更多完整答案,请扫码查看


