《2025年练习生高中数学选择性必修第二册人教B版》

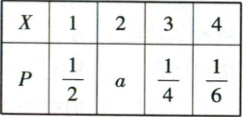
11. [2023·江西赣州高二期末]若随机变量的分布列如下表,则 $ P(|X - 3| = 1) $ 的值为(C)


A.$ \frac{1}{6} $
B.$ \frac{5}{12} $
C.$ \frac{1}{4} $
D.$ \frac{1}{3} $

答案： 11. C 【解析】$|X - 3| = 1 \to X = 2,4 \to P(|X - 3| = 1)=1 - [P(X = 1)+P(X = 3)]$，求解即可。
【解析】根据题意可得，$P(|X - 3| = 1)=P(X = 2)+P(X = 4)=1 - [P(X = 1)+P(X = 3)]=1 - \left(\frac{1}{2}+\frac{1}{4}\right)=\frac{1}{4}$。故选 C。

12. 两对孪生兄弟共 4 人随机排成一排,设随机变量 $ ξ $ 表示孪生兄弟相邻的对数,则(B)

A.$ P(ξ = 0) ＞ P(ξ = 1) $
B.$ P(ξ = 0) = P(ξ = 1) $
C.$ P(ξ = 0) ＜ P(ξ = 1) $
D.$ P(ξ = 1) ＞ P(ξ = 2) $

答案： 12. B 【解析】$4$人排成一排共有$\mathrm{A}_4^4 = 24$（种）不同的排法。$\xi$的所有可能取值为$0,1,2$，所以$P(\xi = 0)=\frac{2\mathrm{A}_2^2\mathrm{A}_2^2}{24}=\frac{1}{3}$，$P(\xi = 1)=\frac{\mathrm{C}_2^1\mathrm{A}_2^2\mathrm{A}_2^2}{24}=\frac{1}{3}$，$P(\xi = 2)=\frac{\mathrm{A}_2^2\mathrm{A}_2^2\mathrm{A}_2^2}{24}=\frac{1}{3}$，所以$P(\xi = 0)=P(\xi = 1)=P(\xi = 2)$。故选 B。

13. [2023·河北沧州高二期末]已知随机变量 $ X $ 的分布列如下表,其中 $ a,b,c $ 成等差数列,则 $ abc $ 的最大值是(C)


A.$ \frac{1}{9} $
B.$ \frac{1}{16} $
C.$ \frac{1}{27} $
D.$ \frac{1}{32} $

答案： 13. C 【解析】由分布列的性质，得$a + b + c = 1$。又$a,b,c$成等差数列，所以$2b = a + c$，所以$b = \frac{1}{3}$，$a + c = \frac{2}{3}$，所以$abc = \frac{1}{3}ac \leq \frac{1}{3}\left(\frac{a + c}{2}\right)^2 = \frac{1}{27}$（利用基本不等式求最值），当且仅当$a = c = \frac{1}{3}$时等号成立，所以$abc$的最大值是$\frac{1}{27}$。故选 C。

14. (多选)[2023·辽宁阜新高二期末]设随机变量 $ ξ $ 的分布列为 $ P(ξ = \frac{k}{5}) = ak $ ($ k = 1,2,3,4,5 $),则(AB)

A.$ a = \frac{1}{15} $
B.$ P(\frac{1}{2} ＜ ξ ＜ \frac{4}{5}) = \frac{1}{5} $
C.$ P(\frac{1}{10} ＜ ξ ＜ \frac{1}{2}) = \frac{2}{15} $
D.$ P(ξ≥\frac{2}{5}) = \frac{3}{10} $

答案： 14. AB 【解析】由题意，得$P\left(\xi = \frac{1}{5}\right)+P\left(\xi = \frac{2}{5}\right)+P\left(\xi = \frac{3}{5}\right)+P\left(\xi = \frac{4}{5}\right)+P(\xi = 1)=a + 2a + 3a + 4a + 5a = 15a = 1$，解得$a = \frac{1}{15}$，故 A 正确；$P\left(\frac{1}{2} ＜ \xi ＜ \frac{4}{5}\right)=P\left(\xi = \frac{3}{5}\right)=3 × \frac{1}{15}=\frac{1}{5}$，故 B 正确；易知$P\left(\frac{1}{10} ＜ \xi ＜ \frac{1}{2}\right)=P\left(\xi = \frac{1}{5}\right)+P\left(\xi = \frac{2}{5}\right)=\frac{1}{15}+2 × \frac{1}{15}=\frac{1}{5}$，故 C 错误；$P\left(\xi \geq \frac{2}{5}\right)=1 - P\left(\xi = \frac{1}{5}\right)=1 - \frac{1}{15} × 1 = \frac{14}{15}$，故 D 错误。选 AB。

$15. [2023·$江西吉安永丰中学高二期末$]$随机变量$ X $的分布列如下表$,$其中$ a,b,c $满足$ a + c = 2b ,$则$ P(|X| = 1) = $　　$\frac{2}{3}$　　$.$　　

答案： 15. $\boldsymbol{\frac{2}{3}}$ 【解析】因为$a + c = 2b$，所以$a + b + c = 3b = 1$，所以$b = \frac{1}{3}$，$a + c = \frac{2}{3}$，所以$P(|X| = 1)=P(X = -1)+P(X = 1)=a + c = \frac{2}{3}$。

16. [2022·山西运城发展联盟高二联考]设随机变量 $ X $ 服从两点分布,若 $ P(X = 1) - P(X = 0) = 0.4 $,则 $ P(X = 1) = $0.7.

答案： 16. 0.7 【解析】由于随机变量$X$服从两点分布，故$P(X = 1)+P(X = 0)=1$①。又$P(X = 1) - P(X = 0)=0.4$②，①+②得$2P(X = 1)=1.4$，所以$P(X = 1)=0.7$。

17. [2023·陕西西安高二期末]如图,小明家住 H 小区,他每天早上骑自行车去 C 学校上学,从家到学校有 $ L_1,L_2 $ 两条路线,$ L_1 $ 路线上有 $ A_1,A_2,A_3 $ 三个路口,每个路口遇到红灯的概率均为 $ \frac{1}{2} $;$ L_2 $ 路线上有 $ B_1,B_2 $ 两个路口,且 $ B_1,B_2 $ 路口遇到红灯的概率分别为 $ \frac{3}{4},\frac{3}{5} $.

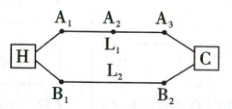
(1)若走 $ L_1 $ 路线,求遇到 3 次红灯的概率;
(2)若走 $ L_2 $ 路线,$ X $ 表示遇到红灯的次数,求 $ X $ 的分布列.

答案： 17.【解】
(1)设“走$\mathrm{L}_1$路线遇到$3$次红灯”为事件$A$，则$P(A)=\frac{1}{2} × \frac{1}{2} × \frac{1}{2}=\frac{1}{8}$。
(2)依题意，$X$的可能取值为$0,1,2$。
则$P(X = 0)=\left(1 - \frac{3}{4}\right) × \left(1 - \frac{3}{5}\right)=\frac{1}{10}$，$P(X = 1)=\frac{3}{4} × \left(1 - \frac{3}{5}\right)+\left(1 - \frac{3}{4}\right) × \frac{3}{5}=\frac{9}{20}$，$P(X = 2)=\frac{3}{4} × \frac{3}{5}=\frac{9}{20}$。
所以随机变量$X$的分布列为
| $X$ | 0 | 1 | 2 |
| --- | --- | --- | --- |
| $P$ | $\frac{1}{10}$ | $\frac{9}{20}$ | $\frac{9}{20}$ |